Nella precedente lezione sull’inferenza bayesiana abbiamo introdotto la statistica bayesiana e mostrato come dedurre una proporzione binomiale utilizzando il concetto di distribuzione a priori coniugata. In questa lezione presentiamo la principale famiglia di algoritmi, i Markov Chain Monte Carlo (MCMC), che ci aiutano ad approssimare la distribuzione a posteriori derivata dal teorema di Bayes.
Abbiamo già spiegato che non tutti i modelli possono usare la distribuzione a priori coniugata, quindi dobbiamo approssimare numericamente la distribuzione a posteriori. In questa lezione introduciamo l’algoritmo Metropolis, semplice da enunciare e da comprendere. Rappresenta il punto di partenza per esplorare MCMC prima di passare ad algoritmi più avanzati come Metropolis-Hastings, Gibbs Sampler e Hamiltonian Monte Carlo.
Dopo aver illustrato il funzionamento di MCMC, mostriamo come usare la libreria open-source PyMC3, che gestisce i dettagli tecnici e ci permette di concentrarci sulla modellazione bayesiana.
Obiettivi dell’inferenza bayesiana
Miriamo a produrre strategie di trading quantitative basate su modelli bayesiani. Per farlo, dobbiamo introdurre una base teorica solida sulla statistica bayesiana. Finora abbiamo trattato:
- La filosofia bayesiana, che usa il teorema di Bayes per aggiornare le credenze sulle probabilità a partire da nuovi dati
- Il ricorso alla distribuzione a priori coniugata per semplificare il calcolo della distribuzione a posteriori nel caso della proporzione binomiale
In questa lezione spieghiamo come usare MCMC per calcolare la distribuzione a posteriori quando non possiamo applicare priori coniugate.
Dopo aver introdotto MCMC, esploriamo campionatori più sofisticati tramite PyMC3 e li applichiamo a modelli complessi. Infine, valutiamo se i modelli riescono a fornire previsioni utili sui rendimenti degli asset. A quel punto, possiamo cominciare a costruire un modello di trading basato sull’analisi bayesiana.
Il Markov Chain Monte Carlo
Nella lezione precedente abbiamo discusso la distribuzione a priori coniugata, che semplifica il calcolo della distribuzione a posteriori tramite Bayes. Sorge allora una domanda: perché serve MCMC se possiamo usare le distribuzioni coniugate?
Dobbiamo ricorrere al Markov Chain Monte Carlo perché molti modelli non si esprimono facilmente in termini di priori coniugate. I modelli complessi, come quelli gerarchici con centinaia di parametri, risultano inaccessibili con metodi analitici.
Ricordando la regola di Bayes:
\(\begin{eqnarray}P(\theta | D) = \frac{P(D | \theta) P(\theta)}{P(D)}\end{eqnarray}\)
Per calcolare l’evidenza \(P(D)\), dobbiamo valutare questo integrale su tutti i possibili \(\theta\):
\(\begin{eqnarray}P(D) = \int_{\Theta} P(D, \theta) \text{d}\theta\end{eqnarray}\)
Il problema principale consiste nella difficoltà di risolvere analiticamente questo integrale, perciò dobbiamo ricorrere a metodi numerici.
Un altro ostacolo riguarda l’elevato numero di parametri nei modelli. Questo implica che le distribuzioni a priori (e quindi a posteriori) potrebbero avere molte dimensioni, rendendo complesso il calcolo dell’integrale in spazi così ampi.
Chiamiamo questa situazione Maledizione della Dimensionalità. In parole semplici, gli spazi ad alta dimensione sono così vasti che i dati risultano radi e poco significativi. Per ottenere inferenze attendibili, serve un volume di dati che cresce in modo esponenziale con il numero di dimensioni.
Algoritmi di Monte Carlo della catena di Markov
Affrontare questo problema richiede strategie intelligenti. I metodi MCMC permettono una ricerca efficiente in spazi di alta dimensione, rendendo gestibili anche modelli bayesiani molto complessi.
L’idea è campionare dalla distribuzione a posteriori combinando una ricerca casuale (Monte Carlo) con un meccanismo di salto intelligente e privo di memoria (proprietà di Markov). Così, MCMC effettua ricerche intelligenti senza memoria.
MCMC non serve solo alla statistica bayesiana. Trova largo impiego anche nella fisica e biologia computazionale per approssimare integrali ad alta dimensione.
Il Markov Chain Monte Carlo non rappresenta un singolo metodo, ma una famiglia di algoritmi. In questa lezione ci concentriamo sull’algoritmo Metropolis. Nei prossimi articoli esamineremo Metropolis-Hastings, Gibbs Sampler, Hamiltonian MCMC e NUTS (No-U-Turn Sampler), già integrato in PyMC3, la libreria che utilizziamo per stimare numericamente la proporzione binomiale.
L’algoritmo Metropolis
Trattiamo per primo l’algoritmo MCMC proposto da Metropolis (1953). Anche se datato, resta valido per comprendere i concetti base e prepara il terreno per campionatori più complessi.
Gli algoritmi MCMC seguono in genere questa struttura (vedi Metodi bayesiani per hacker):
- Inizia nella posizione corrente nello spazio dei parametri (\(\theta_{\text{current}}\))
- Propone un salto verso una nuova posizione (\(\theta_{\text{new}}\))
- Decide in modo probabilistico se accettare o meno il salto
- Se accetta, si sposta nella nuova posizione e ripete dal punto 1
- Se rifiuta, resta nella posizione attuale e ripete dal punto 1
- Dopo un certo numero di iterazioni, restituisce le posizioni accettate
Le differenze principali tra algoritmi MCMC riguardano il modo di saltare e il criterio di accettazione.
L’algoritmo Metropolis propone un salto tramite una distribuzione normale, centrata sulla posizione corrente μ e con una deviazione standard σ detta larghezza della proposta.
La larghezza della proposta influenza fortemente la convergenza. Una proposta ampia esplora più rapidamente lo spazio, ma rischia di saltare regioni ad alta probabilità. Una proposta stretta esplora più lentamente e richiede più tempo.
La distribuzione normale si adatta bene a parametri continui, perché tende a proporre salti vicini ma consente salti più lontani per esplorare lo spazio.
Formula
Dopo aver proposto un salto, dobbiamo decidere in modo probabilistico se accettarlo. Calcoliamo il rapporto tra la probabilità della nuova posizione e quella dell’attuale:
\(\begin{eqnarray}p = P(\theta_{\text{new}})/P(\theta_{\text{current}})\end{eqnarray}\)
Generiamo quindi un numero casuale tra 0 e 1. Se il numero rientra in [0, p], accettiamo il salto; altrimenti, lo rifiutiamo.
Questo algoritmo, sebbene semplice, ci aiuta a evitare il calcolo diretto dell’integrale di evidenza \(P(D)\).
Come spiega Thomas Wiecki, dividendo il posteriore della nuova posizione per quello della corrente, eliminiamo l’evidenza \(P(D)\):
\(\begin{eqnarray}\frac{P(\theta_{\text{new}}|D)}{P(\theta_{\text{current}}|D)} = \frac{\frac{P(D|\theta_{\text{new}})P(\theta_{\text{new}})}{P(D)}}{\frac{P(D|\theta_{\text{current}})P(\theta_{\text{current}})}{P(D)}} = \frac{P(D|\theta_{\text{new}})P(\theta_{\text{new}})}{P(D|\theta_{\text{current}})P(\theta_{\text{current}})}\end{eqnarray}\)
Il risultato finale contiene solo la verosimiglianza e la distribuzione a priori, entrambe calcolabili facilmente. In questo modo, MCMC esplora le regioni a maggiore probabilità a posteriori, riflettendo in pieno la distribuzione dei dati.
Introduzione a PyMC3
PyMC3 è una libreria Python dedicata alla “Programmazione Probabilistica”. Permette di definire modelli probabilistici ed eseguire l’inferenza bayesiana utilizzando diversi metodi Markov Chain Monte Carlo. In questo senso, funziona in modo simile ai pacchetti JAGS e Stan. PyMC3 vanta una lunga lista di collaboratori e riceve aggiornamenti costanti.
Gli sviluppatori di PyMC3 hanno adottato una sintassi chiara che semplifica la definizione dei modelli e riduce al minimo il codice “boilerplate”. La libreria offre classi per tutte le principali distribuzioni di probabilità, e consente di aggiungere facilmente distribuzioni specialistiche. Include una suite potente e diversificata di algoritmi di campionamento Markov Chain Monte Carlo, come l’algoritmo Metropolis, già trattato in precedenza, e il No-U-Turn Sampler (NUTS). Questi strumenti permettono di modellare strutture complesse con migliaia di parametri.
PyMC3 sfrutta la libreria Theano, spesso impiegata nel Deep Learning ad alta intensità computazionale, per massimizzare l’efficienza e la velocità di esecuzione.
Abbiamo trattato Theano nel corso dedicato al Deep Learning applicato al trading quantitativo.
In questa lezione utilizziamo PyMC3 per affrontare un semplice esempio di inferenza su una proporzione binomiale. L’obiettivo è chiarire le idee principali, evitando di complicare il discorso con i dettagli tecnici dell’implementazione del Markov Chain Monte Carlo. Negli articoli successivi esploreremo le funzionalità avanzate di PyMC3 per affrontare modelli bayesiani più complessi.
Dedurre una proporzione binomiale con Markov Chain Monte Carlo
Come descritto nella lezione sull’inferenza di una proporzione binomiale usando la distribuzione a priori coniugata, stimiamo l’equità di una moneta tramite una sequenza di lanci.
Il parametro \(\theta \in [0,1]\) descrive l’equità della moneta, dove \(\theta=0.5\) indica una moneta perfettamente equilibrata.
Abbiamo scelto di utilizzare la distribuzione beta per modellare la nostra convinzione iniziale sull’equità della moneta, grazie alla sua flessibilità. Abbiamo simulato i lanci con una distribuzione di Bernoulli e ottenuto una distribuzione beta anche per il posteriore. Questo tipo di relazione rappresenta un classico esempio di distribuzione a priori coniugata.
Va chiarito che in questo caso non serve utilizzare il Markov Chain Monte Carlo, poiché esiste una soluzione analitica in forma chiusa. Tuttavia, poiché la maggior parte dei modelli bayesiani reali non ammette una soluzione esatta, l’uso di MCMC diventa indispensabile.
Applichiamo MCMC a questo esempio, per confrontare i risultati dell’approssimazione numerica con la soluzione analitica.
Riepilogo dell’inferenza di una proporzione binomiale con la distribuzione a priori coniugata
Nella lezione precedente abbiamo formulato una convinzione a priori: riteniamo che la moneta sia equa, ma non con assoluta certezza. Abbiamo quindi assegnato a \(\theta\) una media \(\mu=0.5\) e una deviazione standard \(\sigma=0.1\).
Per caratterizzare questa convinzione abbiamo usato una distribuzione beta, con parametri \(\alpha\) e \(\beta\). I valori \(\mu=0.5\) e \(\sigma=0.1\) corrispondono a \(\alpha=12\) e \(\beta=12\) (vedi la lezione precedente per i dettagli).
Abbiamo eseguito 50 lanci e osservato 10 teste. Inserendo questi valori nella formula della distribuzione beta a posteriori, abbiamo ottenuto \(\alpha=22\) e \(\beta=52\). Di seguito mostriamo il grafico che confronta le due distribuzioni.
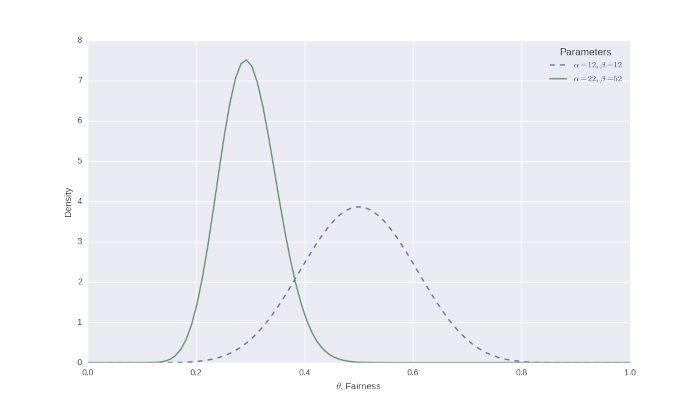
Possiamo intuitivamente vedere come la massa della probabilità si è spostata drasticamente a più vicino a 0,2, che è l’equità del campione dai nostri lanci. Da notare anche che il picco è diventato più stretto poiché siamo ora abbastanza fiduciosi nei nostri risultati, dopo aver effettuato 50 lanci.
Dedurre una proporzione binomiale con PyMC3
Effettuiamo la stessa analisi utilizzando invece il metodo numerico Markov Chain Monte Carlo. Innanzitutto, dobbiamo installare PyMC3:
pip install --process-dependency-links git+https://github.com/pymc-devs/pymc3
Una volta installato, dobbiamo importare le librerie necessarie, che includono Matplotlib, Numpy, Scipy e lo stesso PyMC3. Abbiamo anche impostato lo stile grafico dell’output di Matplotlib in modo che sia simile alla libreria grafica ggplot2:
import matplotlib.pyplot as plt
import numpy as np
import pymc3
import scipy.stats as stats
plt.style.use("ggplot")
Il prossimo passo è impostare i nostri parametri precedenti, così come il numero di prove di lancio di monete effettuate e le teste restituite. Specifichiamo anche, per completezza, i parametri della distribuzione beta calcolata analiticamente a posteriori, che utilizzeremo per il confronto con il nostro approccio Markov Chain Monte Carlo. Inoltre precisiamo di voler effettuare 100.000 iterazioni dell’algoritmo Metropolis:
# Parameter values for prior and analytic posterior
n = 50
z = 10
alpha = 12
beta = 12
alpha_post = 22
beta_post = 52
# How many iterations of the Metropolis
# algorithm to carry out for MCMC
iterations = 100000
Ora definiamo la distribuzione beta a priori e il modello di probabilità di Bernoulli. PyMC3 fornisce un’API molto pulita per farlo. Usiamo un context with di Python per assegnare tutti i parametri, le dimensioni dei passaggi e i valori iniziali a un’istanza di pymc3.Model, che chiamiamo basic_model, seguendo il tutorial ufficiale di PyMC3.
Implementazione
Per prima cosa specifichiamo il parametro theta come distribuzione beta, utilizzando i valori a priori alpha e beta come parametri. Ricordiamo che \(\alpha=12\) e \(\beta=12\) implicano una media a priori \(\mu=0.5\) e una deviazione standard \(\sigma=0.1\).
Definiamo poi la funzione di verosimiglianza di Bernoulli, impostando il parametro di equità p=theta, il numero di prove n=n e le teste osservate observed=z, in base ai parametri già specificati.
A questo punto usiamo l’ottimizzazione MAP (Maximum A Posteriori) di PyMC3 per trovare un valore iniziale ottimale del Markov Chain Monte Carlo per l’algoritmo Metropolis. Approfondiremo questo argomento negli articoli successivi. Successivamente, specifichiamo il campionatore Metropolis e richiamiamo la funzione sample(..) per ottenere i risultati, che memorizziamo nella variabile trace.
# Use PyMC3 to construct a model context
basic_model = pymc3.Model()
with basic_model:
# Define our prior belief about the fairness
# of the coin using a Beta distribution
theta = pymc3.Beta("theta", alpha=alpha, beta=beta)
# Define the Bernoulli likelihood function
y = pymc3.Binomial("y", n=n, p=theta, observed=z)
# Carry out the MCMC analysis using the Metropolis algorithm
# Use Maximum A Posteriori (MAP) optimisation as initial value for MCMC
start = pymc3.find_MAP()
# Use the Metropolis algorithm (as opposed to NUTS or HMC, etc.)
step = pymc3.Metropolis()
# Calculate the trace
trace = pymc3.sample(iterations, step, start, random_seed=1, progressbar=True)
La specifica del modello tramite l’API di PyMC3 ricalca quasi perfettamente quella matematica, mantenendo un codice “boilerplate” minimo. Negli articoli successivi mostreremo tutta la potenza di questa API applicandola a modelli più complessi.
Dopo aver definito e campionato il modello, tracciamo i risultati. Creiamo un istogramma della traccia, ovvero l’elenco di tutti i campioni accettati dal campionamento Markov Chain Monte Carlo, utilizzando 50 bin. Successivamente tracciamo le distribuzioni beta analitiche, sia quella precedente che quella a posteriori, impiegando il metodo stats.beta.pdf(..) di SciPy. Infine, aggiungiamo alcune etichette al grafico e lo visualizziamo.
# Plot the posterior histogram from MCMC analysis
bins=50
plt.hist(
trace["theta"], bins,
histtype="step", normed=True,
label="Posterior (MCMC)", color="red"
)
# Plot the analytic prior and posterior beta distributions
x = np.linspace(0, 1, 100)
plt.plot(
x, stats.beta.pdf(x, alpha, beta),
"--", label="Prior", color="blue"
)
plt.plot(
x, stats.beta.pdf(x, alpha_post, beta_post),
label='Posterior (Analytic)', color="green"
)
# Update the graph labels
plt.legend(title="Parameters", loc="best")
plt.xlabel("$\\theta$, Fairness")
plt.ylabel("Density")
plt.show()
Applied logodds-transform to theta and added transformed theta_logodds to model.
[----- 14% ] 14288 of 100000 complete in 0.5 sec
[---------- 28% ] 28857 of 100000 complete in 1.0 sec
[---------------- 43% ] 43444 of 100000 complete in 1.5 sec
[-----------------58%-- ] 58052 of 100000 complete in 2.0 sec
[-----------------72%------- ] 72651 of 100000 complete in 2.5 sec
[-----------------87%------------- ] 87226 of 100000 complete in 3.0 sec
[-----------------100%-----------------] 100000 of 100000 complete in 3.4 sec
Chiaramente, il tempo di campionamento dipenderà dalla velocità del tuo computer. L’output grafico dell’analisi è riportato nella seguente immagine:
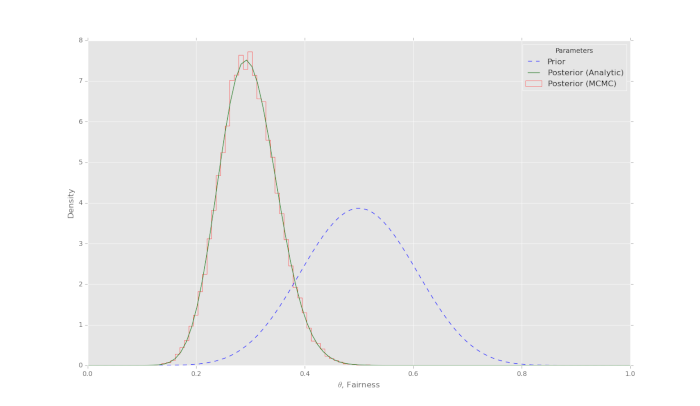
Risultati
In questo esempio con un modello a parametro singolo e 100.000 campioni, l’algoritmo Metropolis mostra un’eccellente convergenza. L’istogramma riproduce fedelmente la distribuzione a posteriori calcolata analiticamente, proprio come previsto. Anche se in un modello così semplice bastano molti meno campioni, l’esperimento evidenzia chiaramente la capacità di convergenza dell’algoritmo Metropolis.
Possiamo introdurre anche il concetto di traccia: il vettore dei campioni generati dal processo di campionamento Markov Chain Monte Carlo. Il metodo traceplot permette di visualizzare sia una stima della densità del kernel (KDE) dell’istogramma mostrato sopra, sia la traccia dei campioni.
Il trace plot offre uno strumento fondamentale per valutare la convergenza di un algoritmo MCMC e per determinare se conviene scartare un numero iniziale di campioni, noto come burn-in. In altri articoli descriviamo nel dettaglio la traccia, il burn-in e altri aspetti legati alla convergenza, analizzando anche campionatori più avanzati. Per generare la traccia basta chiamare traceplot con la variabile trace.
# Show the trace plot
pymc3.traceplot(trace)
plt.show()
Ecco il tracciato completo:
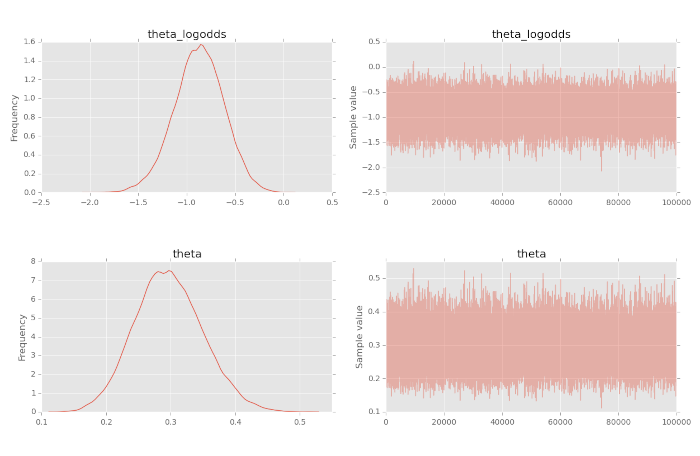
Da notare come la stima di KDE della convinzione a posteriori nell’equità riflette sia la convinzione a priori di \(\sigma=0.5\) che i nostri dati con una correttezza campionaria di \(\sigma=0.2\). Inoltre possiamo vedere che la procedura di campionamento Markov Chain Monte Carlo è “convergente alla distribuzione” poiché la serie di campionamento sembra stazionaria.
In casi più complicati, che esaminiamo in altri articoli, dobbiamo considerare un periodo di “burn in” così come i “sottili” risultati per rimuovere l’autocorrelazione, entrambi i quali migliorano la convergenza.
Per completezza, di seguito l’elenco completo:
import matplotlib.pyplot as plt
import numpy as np
import pymc3
import scipy.stats as stats
plt.style.use("ggplot")
# Parameter values for prior and analytic posterior
n = 50
z = 10
alpha = 12
beta = 12
alpha_post = 22
beta_post = 52
# How many iterations of the Metropolis
# algorithm to carry out for MCMC
iterations = 100000
# Use PyMC3 to construct a model context
basic_model = pymc3.Model()
with basic_model:
# Define our prior belief about the fairness
# of the coin using a Beta distribution
theta = pymc3.Beta("theta", alpha=alpha, beta=beta)
# Define the Bernoulli likelihood function
y = pymc3.Binomial("y", n=n, p=theta, observed=z)
# Carry out the MCMC analysis using the Metropolis algorithm
# Use Maximum A Posteriori (MAP) optimisation as initial value for MCMC
start = pymc3.find_MAP()
# Use the Metropolis algorithm (as opposed to NUTS or HMC, etc.)
step = pymc3.Metropolis()
# Calculate the trace
trace = pymc3.sample(iterations, step, start, random_seed=1, progressbar=True)
# Plot the posterior histogram from MCMC analysis
bins=50
plt.hist(
trace["theta"], bins,
histtype="step", normed=True,
label="Posterior (MCMC)", color="red"
)
# Plot the analytic prior and posterior beta distributions
x = np.linspace(0, 1, 100)
plt.plot(
x, stats.beta.pdf(x, alpha, beta),
"--", label="Prior", color="blue"
)
plt.plot(
x, stats.beta.pdf(x, alpha_post, beta_post),
label='Posterior (Analytic)', color="green"
)
# Update the graph labels
plt.legend(title="Parameters", loc="best")
plt.xlabel("$\\theta$, Fairness")
plt.ylabel("Density")
plt.show()
# Show the trace plot
pymc3.traceplot(trace)
plt.show()
Conclusione
In questa lezione abbiamo descritto le basi del Markov Chain Monte Carlo, nonché un metodo specifico noto come algoritmo Metropolis, applicato per dedurre una proporzione binomiale.
Tuttavia, come discusso in precedenza, PyMC3 utilizza un campionatore MCMC molto più sofisticato noto come No-U-Turn Sampler (NUTS). Per capire la logica di questo campionatore, alla fine dobbiamo considerare ulteriori tecniche di campionamento come Metropolis-Hastings, Gibbs Sampling e Hamiltonian Monte Carlo (su cui si basa NUTS).
Vogliamo anche iniziare ad applicare le tecniche di Programmazione Probabilistica a modelli più complessi, come i modelli gerarchici. Questo a sua volta ci aiuterà a produrre sofisticate strategie di trading quantitativo.
Riferimenti
- Davidson-Pilon, C. et al (2016) “Probabilistic Programming & Bayesian Methods for Hackers”, http://camdavidsonpilon.github.io/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/
- Duane, S. et al (1987) “Hybrid Monte Carlo”, Physics Letters B 195 (2): 216–222
- Gelfand, A.E. and Smith, A.F.M. (1990) “Sampling-based approaches to calculating marginal densities”, J. Amer. Statist. Assoc., 85, 140, 398-409.
- Geman, S. and Geman, D. (1984) “Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images.”, IEEE Trans. Pattern Anal. Mach. Intell., 6, 721-741.
- Gelman, A. et al (2013) Bayesian Data Analysis, 3rd Edition, Chapman and Hall/CRC
- Hastings, W. (1970) “Monte Carlo sampling methods using Markov chains and their application”, Biometrika, 57, 97-109.
- Hoffman, M.D., and Gelman, A. (2011) “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo, arXiv:1111.4246 [stat.CO]
- Kruschke, J. (2014) Doing Bayesian Data Analysis, Second Edition: A Tutorial with R, JAGS, and Stan, Academic Press
- Metropolis, N. et al (1953) “Equations of state calculations by fast computing machines”, J. Chem. Phys., 21, 1087-1092.
- Robert, C. and Casella, G. (2011) “A Short History of Markov Chain Monte Carlo: Subjective Recollections from Incomplete Data”, Statistical Science 0, 00, 1-14.
- Wiecki, T. (2015) “MCMC sampling for dummies”, http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/

