In questa lezione introduciamo il concetto di inferenza tramite l’approccio bayesiano, partendo dall’esempio del lancio di una moneta descritto nella lezione precedente. Approfondiamo le nozioni legate alle prove di Bernoulli, alla distribuzione beta e alla distribuzione a priori coniugata.
Nella precedente lezione abbiamo esaminato la regola di Bayes e spiegato come aggiorna razionalmente le convinzioni sull’incertezza alla luce di nuove evidenze. Abbiamo anche accennato al ruolo crescente di queste tecniche nella data science e nella finanza quantitativa.
In questa lezione ci concentriamo su come applicare l’inferenza bayesiana su una proporzione binomiale, ovvero analizzare situazioni con due possibili esiti (come testa o croce nel lancio di una moneta) e stimare la proporzione di un certo risultato su più eventi ripetuti.
Il nostro obiettivo è stimare quanto sia equa una moneta. Questa stima ci consente di prevedere la probabilità che esca testa nei lanci futuri.
Anche se l’esempio può sembrare accademico, risulta altamente applicabile in diversi contesti reali. Ecco alcuni esempi:
- Ingegneria: stimare la proporzione di pale delle turbine aeronautiche con difetti strutturali dopo la produzione.
- Scienze sociali: stimare la percentuale di persone che rispondono “sì” a una domanda di censimento.
- Scienza medica: stimare la percentuale di pazienti che guariscono completamente dopo aver assunto un farmaco sperimentale.
- Finanza aziendale: stimare la percentuale di transazioni errate rilevate durante un audit finanziario.
- Data Science: stimare la percentuale di utenti che cliccano su un annuncio visitando un sito web.
L’inferenza bayesiana su una proporzione binomiale rappresenta una tecnica statistica essenziale, alla base di molte applicazioni avanzate della statistica bayesiana.
L’approccio Bayesiano
Dopo aver introdotto la statistica bayesiana nella lezione precedente, ora delineiamo il processo analitico dell’approccio bayesiano.
Stimiamo l’equità di una moneta e utilizziamo questa stima per prevedere quante volte uscirà testa nei prossimi lanci.
Nel farlo, analizziamo i seguenti passaggi:
- Presupposti: supponiamo che la moneta abbia solo due esiti possibili (testa o croce), che i lanci siano indipendenti e casuali, e che l’equità della moneta (indicata con il parametro θ) resti invariata nel tempo.
- Credenze precedenti: esprimiamo le convinzioni iniziali sull’equità della moneta attraverso una distribuzione di probabilità, usando una distribuzione beta per modellarle.
- Dati sperimentali: raccogliamo dati da una serie di lanci (N) e contiamo le volte in cui esce testa (z). Per valutare la probabilità di questi risultati dati θ, introduciamo la funzione di verosimiglianza di Bernoulli.
- Credenze a posteriori: combiniamo la distribuzione a priori e la funzione di verosimiglianza tramite la regola di Bayes per ottenere la distribuzione a posteriori sull’equità della moneta. Usando una distribuzione beta come a priori e un modello di Bernoulli, otteniamo nuovamente una distribuzione beta a posteriori, grazie alla proprietà delle distribuzioni coniugate.
- Inferenza: stimiamo θ (l’equità della moneta), calcoliamo la probabilità di testa al prossimo lancio, e analizziamo come cambiano i risultati variando le credenze precedenti (confronto tra modelli).
In ogni fase, visualizziamo graficamente le funzioni e le distribuzioni utilizzando il pacchetto Seaborn di Python, basato su Matplotlib, ideale per la rappresentazione statistica. Dai un’occhiata a questa gallery per scoprire le sue potenzialità.
Presupposti dell’approccio bayesiano
Ogni modello statistico richiede ipotesi. Nel caso dell’approccio bayesiano:
- La moneta ha due soli esiti: testa o croce.
- I lanci sono indipendenti e identicamente distribuiti.
- La correttezza della moneta è stazionaria, ossia costante nel tempo.
Partendo da questi presupposti, possiamo applicare l’inferenza bayesiana.
La Regola di Bayes
Nella lezione precedente abbiamo introdotto la regola di Bayes:
La Regola di Bayes applicata all’Inferenza Bayesiana
\(
\begin{eqnarray}
P(\theta|D) = \frac{P(D|\theta) \cdot P(\theta)}{P(D)}
\end{eqnarray}
\)
Definiamo i componenti:
- P(θ): probabilità a priori, ossia la nostra convinzione iniziale su θ (es. che la moneta sia equa).
- P(θ|D): probabilità a posteriori, ovvero la convinzione aggiornata dopo aver osservato i dati D (es. 4 teste su 8 lanci).
- P(D|θ): verosimiglianza, la probabilità di osservare i dati D dato un certo valore di θ.
- P(D): evidenza, una costante di normalizzazione che rappresenta la probabilità complessiva di osservare i dati D.
Per calcolare la probabilità a posteriori, specifichiamo tre componenti: verosimiglianza, probabilità a priori ed evidenza. Le sezioni seguenti spiegano come definire ciascun elemento per il caso dell’inferenza su una proporzione binomiale.
La funzione di Verosimiglianza
La Distribuzione di Bernoulli
Immagina una sequenza di lanci di una moneta: l’obiettivo è calcolare la probabilità che esca “testa”, in funzione del parametro di equità θ.
Questa probabilità assume una forma funzionale, indicata con f. Se chiamiamo k la variabile casuale che descrive l’esito del lancio, con k ∈ {1, 0} (dove k = 1 indica “testa” e k = 0 indica “croce”), allora la probabilità di ottenere “testa”, dato θ, è:
\(
\begin{eqnarray}
P(k = 1 | \theta) = f(\theta)
\end{eqnarray}
\)
Possiamo scegliere una forma semplice per f(θ), affermando che f(θ) = θ. Quindi la probabilità di ottenere “testa” è:
\(
\begin{eqnarray}
P(k = 1 | \theta) = \theta
\end{eqnarray}
\)
E la probabilità di ottenere “croce” è:
\(
\begin{eqnarray}
P(k = 0 | \theta) = 1-\theta
\end{eqnarray}
\)
Possiamo riassumere entrambe le probabilità in un’unica espressione:
\(
\begin{eqnarray}
P(k | \theta) = \theta^k (1 – \theta)^{1-k}
\end{eqnarray}
\)
dove \(k \in \{1, 0\}\) e \(\theta \in [0,1]\).
Questa è la Distribuzione di Bernoulli: una distribuzione discreta che assegna probabilità a due possibili esiti di k per un valore fisso di θ.
In pratica, la distribuzione di Bernoulli quantifica la probabilità che esca “testa” o “croce” in base all’equità della moneta.
La funzione di Verosimiglianza di Bernoulli
Esaminiamo ora un altro punto di vista. Supponiamo di conoscere il risultato k del lancio e di considerare θ come variabile continua. In questo caso, la formula:
\(
\begin{eqnarray}
P(k | \theta) = \theta^k (1 – \theta)^{1-k}
\end{eqnarray}
\)
esprime la probabilità di ottenere un risultato noto k al variare di θ. Cambiando θ (cioè modificando l’equità della moneta), otteniamo probabilità diverse per k.
Questa è la funzione di verosimiglianza di θ: una funzione continua che si distingue dalla distribuzione di Bernoulli, la quale rappresenta invece una distribuzione discreta di probabilità su k.
La funzione di verosimiglianza non rappresenta una vera distribuzione di probabilità, poiché l’integrale su tutti i valori possibili di θ non restituisce 1, come richiesto per una distribuzione.
Chiamiamo quindi \(P(k | \theta) = \theta^k (1 – \theta)^{1-k}\) la funzione di verosimiglianza di Bernoulli rispetto a θ.
Lanci Multipli della moneta
Possiamo usare la funzione di verosimiglianza di Bernoulli per calcolare la probabilità di osservare una sequenza di N lanci, descritta dall’insieme \(\{k_1, …, k_N\}\).
Poiché ogni lancio è indipendente dagli altri, basta moltiplicare le probabilità dei singoli lanci per ottenere la probabilità dell’intera sequenza:
\(
\begin{eqnarray}
P(\{k_1, …, k_N\} | \theta) &=& \prod_{i} P(k_i | \theta) \\
&=& \prod_{i} \theta^{k_i} (1 – \theta)^{1-{k_i}}
\end{eqnarray}
\)
Se ci interessa solo il numero di “teste” ottenute nei N lanci, indichiamo con z il loro numero. La probabilità diventa:
\(
\begin{eqnarray}
P(z, N | \theta) = \theta^z (1 – \theta)^{N-z}
\end{eqnarray}
\)
Questa espressione descrive la probabilità di ottenere z “teste” in N lanci, dato il parametro θ. Utilizzeremo questa formula per calcolare la distribuzione a posteriori, come vedremo più avanti nella lezione.
Quantificare le Credenze a Priori
Un passaggio fondamentale dell’approccio bayesiano consiste nel definire le credenze a priori, ovvero assegnare una probabilità alle ipotesi iniziali e quantificarla.
L’approccio bayesiano richiede di formulare ipotesi sui parametri e scegliere una distribuzione che rappresenti queste convinzioni. In questo caso, vogliamo esprimere l’incertezza sull’equità della moneta, cioè se sia truccata oppure no.
Per farlo, analizziamo l’intervallo dei valori che θ può assumere e assegniamo una probabilità a ciascun valore possibile.
– Se \(\theta = 0\), la moneta dà sempre “croce”.
– Se \(\theta = 1\), la moneta dà sempre “testa”.
– Una moneta equa ha \(\theta = 0,5\).
Quindi \(\theta \in [0,1]\), e la distribuzione di probabilità che usiamo deve coprire questo intervallo.
La domanda ora è: quale distribuzione rappresenta meglio le nostre convinzioni a priori?
Distribuzione Beta
Scegliamo la distribuzione beta, la cui funzione di densità di probabilità è:
\(
\begin{eqnarray}
P(\theta | \alpha, \beta) = \frac{\theta^{\alpha – 1} (1 – \theta)^{\beta – 1}}{B(\alpha, \beta)}
\end{eqnarray}
\)
Nel denominatore, \(B(\alpha, \beta)\) è la costante di normalizzazione che garantisce che l’area sotto la curva sia pari a 1.
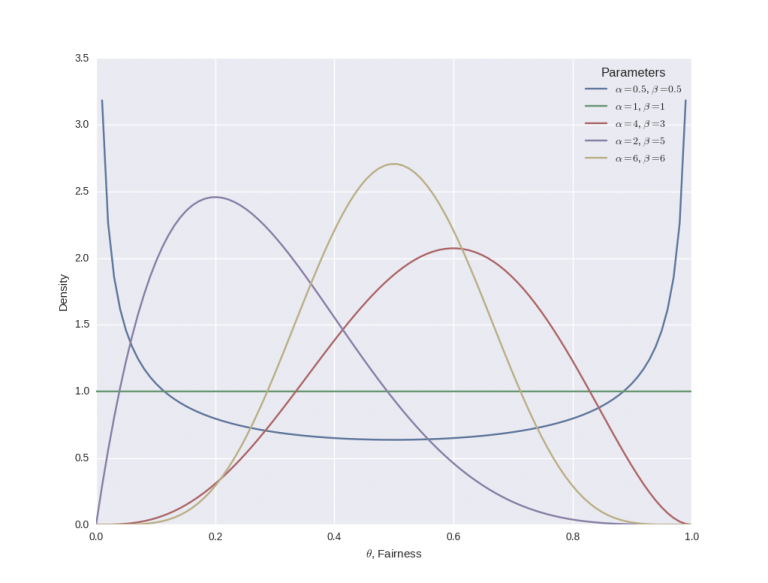
Il grafico seguente mostra come cambia la forma della distribuzione beta al variare dei parametri α e β:
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt
import seaborn as sns
if __name__ == "__main__":
sns.set_palette("deep", desat=.6)
sns.set_context(rc={"figure.figsize": (8, 4)})
x = np.linspace(0, 1, 100)
params = [
(0.5, 0.5),
(1, 1),
(4, 3),
(2, 5),
(6, 6)
]
for p in params:
y = beta.pdf(x, p[0], p[1])
plt.plot(x, y, label="$\\alpha=%s$, $\\beta=%s$" % p)
plt.xlabel("$\\theta$, Fairness")
plt.ylabel("Density")
plt.legend(title="Parameters")
plt.show()
Essenzialmente, quando α diventa più grande, la maggior parte della distribuzione di probabilità si muove verso destra (una moneta truccata per avere più “teste”), mentre un aumento di β sposta la distribuzione verso sinistra (una moneta truccata per avere più “croci”) .
Tuttavia, se si aumenta sia α che β, la distribuzione inizia a restringersi. Se α e β aumentano ugualmente, allora la distribuzione raggiungerà un picco per θ = 0,5, cioè quando la moneta è equa.
Perché si è scelto la funzione beta come probabilità a priori? Ci sono un paio di motivi:
- Supporto – La funzione è definito nell’intervallo [0,1], lo stesso intervallo di esistenza di θ.
- Flessibilità – Possiede due parametri di forma conosciuti come α e β, che gli conferiscono una notevole flessibilità. Questa flessibilità offre una vasta scelta delle modalità per modelliamo le credenze.
Tuttavia, la ragione più importante per scegliere una distribuzione beta è dovuta al fatto che questa è una distribuzione a priori congiunta (conjugate prior) per la distribuzione di Bernoulli.
Distribuzione a Priori Coniugata
Nella regola di Bayes, riportata sopra, è evidente che la distribuzione a posteriori è proporzionale al prodotto della distribuzione precedente e alla funzione di verosimiglianza:
\(
\begin{eqnarray}
P(\theta | D) \propto P(D|\theta) P(\theta)
\end{eqnarray}
\)
Una distribuzione a priori coniugata è una possibile scelta per descrivere la probabilità a priori perché, quando accoppiata con uno specifico tipo di funzione di verosimiglianza, fornisce una distribuzione a posteriori appartenente alla stessa famiglia della distribuzione a priori.
Sia a priori che sia a posteriori hanno la stessa famiglia di distribuzione di probabilità, ma con parametri diversi.
I conjugate prior sono estremamente convenienti dal punto di vista del calcolo poiché forniscono espressioni di forma chiusa per la distribuzione a posteriori, annullando in tal modo qualsiasi complessa integrazione numerica.
Nell’approccio bayesiano, se si usa una funzione di verosimiglianza di Bernoulli e una distribuzione beta come descrivere la probabilità a priori si ottiene immediatamente che la probabilità a posteriori sarà anch’essa una distribuzione beta.
L’utilizzo di una distribuzione beta per la probabilità a priori implica la possibilità di effettuare lanci di monete sperimentali e perfezionare direttamente le convinzioni. La probabilità a posteriori diventerà la nuova probabilità a priori ed è possibile usare la regola di Bayes in successione quando vengono generati nuovi lanci di monete.
Se la precedente credenza è specificata da una distribuzione beta e si ha una funzione di verosimiglianza di Bernoulli, allora anche la probabilità a posteriori sarà anche una distribuzione beta.
Da notare tuttavia che un priore è solo coniugato rispetto a una particolare funzione di probabilità.
Coniugare una Distribuzione Beta con una funzione di Verosimiglianza di Bernoulli
Si può utilizzare un semplice calcolo per dimostrare che scegliere la distribuzione beta per la probabilità a priori, con una verosimiglianza di Bernoulli, fornisce una distribuzione beta per la probabilità a posteriori.
Come accennato in precedenza, la funzione di densità di probabilità di una distribuzione beta, per uno specifico parametro θ, è data da:
\(
\begin{eqnarray}
P(\theta | \alpha, \beta) = \theta^{\alpha – 1} (1 – \theta)^{\beta – 1} / B(\alpha, \beta)
\end{eqnarray}
\)
Da notare che la forma della distribuzione beta è simile alla forma di una verosimiglianza di Bernoulli. Infatti, se si moltiplicano le due forme (come nella regola di Bayes), si ottiene:
\(
\begin{eqnarray}
\theta^{\alpha – 1} (1 – \theta)^{\beta – 1} / B(\alpha, \beta) \times \theta^{k} (1 – \theta)^{1-k} \propto \theta^{\alpha + k – 1} (1 – \theta)^{\beta + k}
\end{eqnarray}
\)
Il termine sul lato destro del segno di proporzionalità ha la stessa forma del prior (a meno di una costante normalizzante).
Differenti modi per specificare una Distribuzione Beta
Finora è stato descritto come utilizzare una distribuzione beta per specificare le convinzioni precedenti relative alla correttezza della moneta. Tuttavia, si hanno solo due parametri con cui giocare, vale a dire α e β.
In che modo questi due parametri corrispondono alla significato più intuitivo di “verosimiglianza” e “incertezza” nella corretta della moneta?
Bene, questi due concetti corrispondono perfettamente alla media e alla varianza della distribuzione beta. Quindi, se si trova una relazione tra questi due valori e i parametri α e β, si può più facilmente specificare le nostre convinzioni.
Si scopre (vedi l’articolo di Wikipedia sulla distribuzione beta) che la media μ è data da:
\(
\begin{eqnarray}
\mu = \frac{\alpha}{\alpha + \beta}
\end{eqnarray}
\)
Mentre la deviazione standard σ è data da:
\(
\begin{eqnarray}
\sigma = \sqrt{\frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}}
\end{eqnarray}
\)
Quindi, riorganizzando queste formule per fornire α e β in termini di μ e σ. α si ottiene:
\(
\begin{eqnarray}
\alpha = \left( \frac{1-\mu}{\sigma^2} – \frac{1}{\mu} \right) \mu^2
\end{eqnarray}
\)
Mentre β è dato da:
\(
\begin{eqnarray}
\beta = \alpha \left( \frac{1}{\mu} – 1 \right)
\end{eqnarray}
\)
In questo passaggio è necessario prestare molta attenzione perché non è possibile specificare un σ > 0,289, dato che questa è la deviazione standard di una densità uniforme (che implica nessuna credenza precedente su ogni specifica equità della moneta).
Ad esempio, se si ipotizza una equità della moneta intorno allo 0,5, ma senza l’assoluta certezza. Si può specificare una deviazione standard di circa 0,1. Quale distribuzione beta sarà prodotta come risultato?
Inserendo i numeri nelle formule si ottine α = 12 e β = 12 e la distribuzione beta è simile alla seguente:
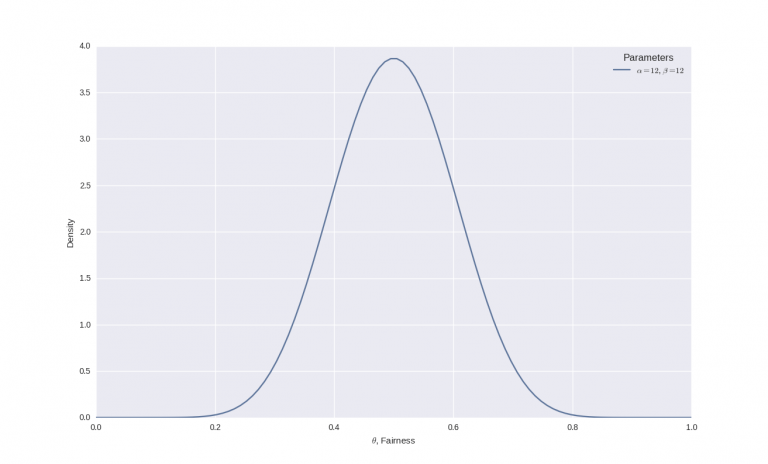
Da notare come, nonostante il picco sia centrato attorno allo 0,5, è presente una significativa incertezza in questa credenza che è rappresentata dalla larghezza della curva.
Conclusione
L’approccio bayesiano nel trading offre un quadro potente e flessibile per aggiornare le convinzioni man mano che emergono nuovi dati, migliorando progressivamente l’affidabilità delle decisioni. Grazie all’uso di distribuzioni a priori coniugate come la beta, è possibile ottenere stime a posteriori in forma chiusa, riducendo la complessità computazionale. Questo consente di adattare dinamicamente le strategie di investimento, modellando l’incertezza e l’evoluzione delle probabilità in modo coerente e interpretabile.

