Su TradingQuant descriviamo diversi aspetti del trading quantitativo, come i modelli di machine learning, l’analisi delle serie temporali, l’implementazione di sistemi di trading e l’uso di ambienti di backtesting. In questa lezione presentiamo la statistica bayesiana nel trading e nella finanza quantitativa.
Queste moderne tecniche matematiche non trovano applicazione solo nel trading algoritmico e nella finanza quantitativa, ma anche nei campi emergenti della scienza dei dati e dell’apprendimento statistico delle macchine.
Le competenze quantitative oggi risultano fondamentali non solo in ambito finanziario, ma anche nelle startup tecnologiche e nelle grandi aziende che si occupano di analisi dei dati.
Prima di approfondire le tecniche più avanzate (“bleeding edge”), è essenziale comprendere le teorie matematiche e statistiche alla base di questi modelli. Una di queste è la statistica bayesiana. Fino ad ora, su questo sito non avevamo ancora trattato i metodi bayesiani. Abbiamo scritto questo articolo proprio per aiutarti a comprendere la filosofia dell’approccio bayesiano, confrontarlo con il metodo classico e scoprire le sue applicazioni nella finanza quantitativa e nella scienza dei dati.
In particolare, in questa lezione:
- Definiamo la statistica bayesiana (o inferenza bayesiana)
- Confrontiamo la statistica classica con quella bayesiana
- Spieghiamo la regola di Bayes, strumento chiave dell’inferenza bayesiana
- Applichiamo la regola di Bayes per trarre inferenze
- Mostriamo un esempio pratico: il lancio di una moneta truccata
La Statistica Bayesiana
La statistica bayesiana rappresenta un approccio che applica la probabilità ai problemi statistici. Usa strumenti matematici per stimare la probabilità di eventi incerti in base al grado di fiducia (o credibilità) che assegniamo loro.
L’inferenza bayesiana considera la probabilità come una misura soggettiva della fiducia nel verificarsi di un evento. Le convinzioni iniziali possono cambiare quando nuove prove emergono. La statistica bayesiana fornisce un modello formale per aggiornare queste convinzioni.
A differenza della statistica classica, che basa le probabilità sulla frequenza degli eventi in prove ripetute, la statistica bayesiana aggiorna continuamente le credenze soggettive in base ai nuovi dati.
Per esempio, mentre la statistica frequentista analizza il lancio di un dado in termini di frequenze a lungo termine, la statistica bayesiana valuta come la credenza su un certo risultato cambi man mano che i dati si accumulano.
Frequentista vs Bayesiana
Per chiarire le differenze tra i due approcci, osserviamo due esempi:
- Lancio di una moneta truccata – Qual è la probabilità che esca testa?
- Elezione politica – Qual è la probabilità che un candidato vinca senza precedenti elettorali?
| Esempio | Approccio Frequentista | Approccio Bayesiano |
|---|---|---|
| Moneta truccata | Stima la probabilità di “testa” osservando la frequenza relativa in molti lanci indipendenti. Le credenze personali non influenzano l’analisi. | All’inizio, lanciando poche volte, si suppone che la moneta sia equa. Se però escono più volte “testa”, si modifica la convinzione. Dopo 500 lanci con 400 teste, si conclude che la moneta è probabilmente truccata. |
| Elezione | Simula elezioni virtuali per stimare la frequenza con cui il candidato vince. L’approccio non considera opinioni personali. | Ogni individuo parte con una convinzione personale sulla probabilità di vittoria. Quando arrivano nuovi dati, aggiorna la credenza con la regola di Bayes. Anche opinioni inizialmente divergenti tendono a convergere nel tempo. |
Nel metodo bayesiano, la probabilità riflette l’opinione soggettiva. Due individui intelligenti possono avere convinzioni diverse, ma i dati condivisi portano a credenze convergenti, grazie all’aggiornamento razionale.
La Regola di Bayes
Per eseguire l’inferenza bayesiana, usiamo la regola di Bayes, che si basa sulla probabilità condizionata.
Definizione base:
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
Questa formula calcola la probabilità di A dato B. Se riscriviamo le relazioni con P(B|A), otteniamo:
$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$$
Espandendo P(B) usando tutti i possibili eventi A, otteniamo la versione completa:
$$P(A|B) = \frac{P(B|A) \cdot P(A)}{\sum_{a \in A} P(B|A) \cdot P(A)}$$
Applicazione della Regola di Bayes all’Inferenza
L’inferenza bayesiana aggiorna le convinzioni precedenti ogni volta che riceviamo nuove prove. Per esempio, se credi che la Luna possa schiantarsi sulla Terra, ogni notte passata senza incidente riduce la tua credenza in quel rischio, man mano che nuove osservazioni contrarie si accumulano.
Prova di Bernoulli
Considera una moneta truccata. Il parametro θ indica la probabilità che esca testa: θ ∈ [0,1]. Ogni lancio della moneta rappresenta una prova di Bernoulli: un esperimento con solo due risultati (testa o croce) e probabilità costante.
Dopo alcuni lanci otteniamo dei dati D. Ci chiediamo:
- Qual è la probabilità di ottenere 3 teste su 8 lanci se la moneta è equa (θ = 0.5)?
- Qual è la probabilità che la moneta sia equa dato che abbiamo osservato 4 teste?
La probabilità di osservare D dato θ è: P(D|θ).
Ma l’inferenza bayesiana si interessa a: P(θ|D), cioè la probabilità che θ abbia un certo valore, dato D.
Regola di Bayes nell’Inferenza
$$P(\theta|D) = \frac{P(D|\theta) \cdot P(\theta)}{P(D)}$$
Dove:
- P(θ): probabilità a priori — convinzione iniziale prima dei dati
- P(θ|D): probabilità a posteriori — convinzione aggiornata dopo i dati
- P(D|θ): verosimiglianza dei dati dato il parametro
- P(D): probabilità marginale dei dati
La statistica bayesiana nel trading usa proprio questo processo per affinare i modelli, migliorare le previsioni e gestire l’incertezza nei mercati finanziari.
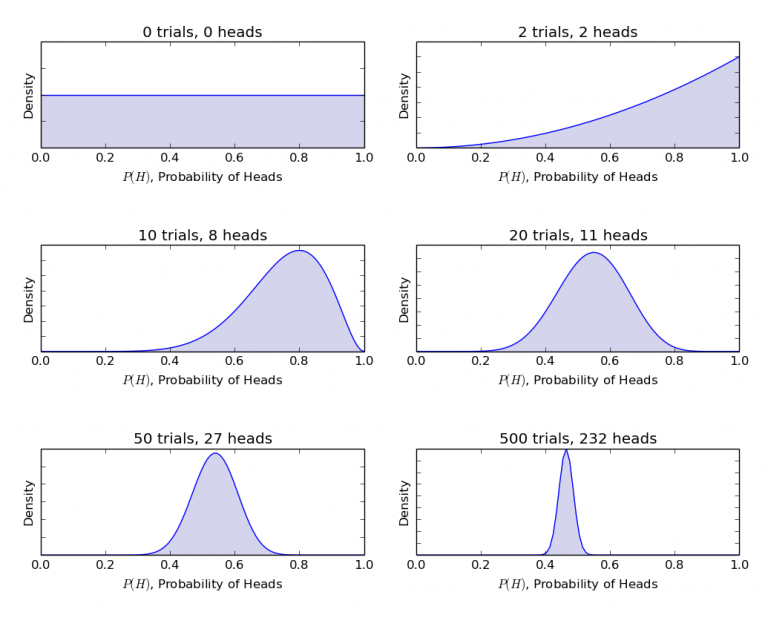
Nei grafici precedenti, l’inferenza bayesiana mostra chiaramente come sia possibile passare da una situazione incerta con dati limitati a una più solida e affidabile grazie all’aggiunta di informazioni. Questo approccio offre una procedura razionale ed efficace per aggiornare le probabilità in base a nuovi dati, rendendo l’inferenza bayesiana uno strumento prezioso nell’analisi statistica.
Per completezza, riportiamo il codice Python (ampiamente commentato) utilizzato per generare il grafico. Il codice sfrutta le funzioni statistiche offerte da SciPy, in particolare la distribuzione Beta:
if __name__ == "__main__":
# Create a list of the number of coin tosses ("Bernoulli trials")
number_of_trials = [0, 2, 10, 20, 50, 500]
# Conduct 500 coin tosses and output into a list of 0s and 1s
# where 0 represents a tail and 1 represents a head
data = stats.bernoulli.rvs(0.5, size=number_of_trials[-1])
# Discretise the x-axis into 100 separate plotting points
x = np.linspace(0, 1, 100)
# Loops over the number_of_trials list to continually add
# more coin toss data. For each new set of data, we update
# our (current) prior belief to be a new posterior. This is
# carried out using what is known as the Beta-Binomial model.
# For the time being, we won't worry about this too much. It
# will be the subject of a later article!
for i, N in enumerate(number_of_trials):
# Accumulate the total number of heads for this
# particular Bayesian update
heads = data[:N].sum()
# Create an axes subplot for each update
ax = plt.subplot(len(number_of_trials) / 2, 2, i + 1)
ax.set_title("%s trials, %s heads" % (N, heads))
# Add labels to both axes and hide labels on y-axis
plt.xlabel("$P(H)$, Probability of Heads")
plt.ylabel("Density")
if i == 0:
plt.ylim([0.0, 2.0])
plt.setp(ax.get_yticklabels(), visible=False)
# Create and plot a Beta distribution to represent the
# posterior belief in fairness of the coin.
y = stats.beta.pdf(x, 1 + heads, 1 + N - heads)
plt.plot(x, y, label="observe %d tosses,\n %d heads" % (N, heads))
plt.fill_between(x, 0, y, color="#aaaadd", alpha=0.5)
# Expand plot to cover full width/height and show it
plt.tight_layout()
plt.show()
Conclusione
Nel prossimo articolo analizzeremo in dettaglio il concetto di distribuzione a priori coniugata, che semplifica notevolmente i calcoli matematici necessari per applicare l’inferenza bayesiana in contesti pratici come quello mostrato in questo esempio.

