Nella lezione precedente abbiamo definito l’analisi delle serie temporali come uno strumento utile per sviluppare strategie di trading. In questa lezione approfondiamo uno degli aspetti più rilevanti delle serie temporali: la correlazione seriale, conosciuta anche come autocorrelazione.
Prima di addentrarci nella definizione di correlazione seriale, analizziamo lo scopo generale della modellazione delle serie temporali e spieghiamo perché focalizzarci sulla correlazione seriale risulta fondamentale.
Introduzione
Quando lavoriamo con una o più serie temporali finanziarie, puntiamo principalmente a prevedere o simulare l’andamento dei dati. Riusciamo facilmente a individuare trend deterministici e variazioni stagionali, e possiamo scomporre la serie in queste componenti. Tuttavia, dopo questa scomposizione, rimane una componente casuale.
In alcuni casi, possiamo modellare bene questa componente con variabili casuali indipendenti. Ma spesso, soprattutto nel contesto finanziario, notiamo che gli elementi consecutivi della serie presentano una correlazione. In altre parole, il comportamento dei punti successivi nella serie risulta dipendente. Un caso tipico lo troviamo nel trading di coppie con ritorno alla media, dove la correlazione tra variabili sequenziali indica il ritorno alla media stesso.
Come modellatori quantitativi, cerchiamo di individuare la struttura di queste correlazioni per migliorare le previsioni e potenziare la redditività di una strategia. Riconoscere tale struttura aumenta anche il realismo delle serie temporali simulate e quindi rafforza l’efficacia delle componenti di gestione del rischio.
Quando osserviamo correlazioni tra dati sequenziali all’interno di una serie temporale, affermiamo che esiste correlazione seriale o autocorrelazione.
Ora che comprendiamo l’utilità di studiare la correlazione seriale, passiamo a definirla in modo matematico. Prima, però, introduciamo alcuni concetti base come aspettativa e varianza.
Aspettativa, varianza e covarianza
Molte di queste definizioni risulteranno familiari alla maggior parte degli utenti di TradingQuant, ma le includiamo per completezza.
Cominciamo con la definizione di valore atteso o aspettativa:
Aspettativa
L’aspettativa di una variabile casuale \(x\), indicata con \(E(x)\), rappresenta il suo valore medio nella popolazione. Denotiamo tale aspettativa con \(\mu\), quindi \(E(x) = \mu\).
Definita l’aspettativa, introduciamo la varianza, che misura la dispersione di una variabile casuale:
Varianza
La varianza rappresenta l’aspettativa delle deviazioni al quadrato dalla media. La indichiamo con \(\sigma^2(x) = E[(x-\mu)^2]\).
La varianza risulta sempre non negativa. Da qui, possiamo definire la deviazione standard:
Deviazione standard
La deviazione standard di una variabile casuale \(x\), indicata con \(\sigma(x)\), corrisponde alla radice quadrata della sua varianza.
Una volta descritte queste definizioni di base, estendiamo la varianza al concetto di covarianza tra due variabili casuali. La covarianza misura il grado di correlazione lineare tra le due:
Covarianza
La covarianza tra due variabili casuali \(x\) e \(y\), con aspettative \(\mu_x\) e \(\mu_y\), si calcola come \(\sigma(x, y) = E[(x – \mu_x)(y – \mu_y)]\).
La covarianza ci indica come le due variabili si muovono congiuntamente.
Nel nostro contesto statistico, non conosciamo i valori della popolazione \(\mu_x\) e \(\mu_y\), quindi stimiamo la covarianza da un campione. Usiamo le medie campionarie \(\bar{x}\) e \(\bar{y}\).
Consideriamo un insieme di \(n\) coppie di osservazioni \((x_i, y_i)\). La covarianza campionaria, indicata con \(\text{Cov}(x, y)\) (talvolta anche come \(q(x, y)\)), si calcola con:
\(\begin{eqnarray} \text {Cov} (x, y) = \frac {1} {n-1} \sum ^ n_ {i = 1} (x_i – \bar {x}) (y_i – \bar { y}) \end{eqnarray}\)
Nota: potremmo chiederci perché dividiamo per \(n-1\) anziché per \(n\). La scelta di \(n-1\) consente di ottenere una stima non distorta della covarianza.
Esempio: Covarianza campionaria in Python
Per calcolare la covarianza possiamo sfruttare la libreria NumPy in Python. NumPy non offre una funzione diretta per la covarianza tra due variabili, ma dispone di una funzione cov() che restituisce una matrice di covarianza. Possiamo estrarre da lì la nostra misura. Di default, cov() calcola la covarianza campionaria.
Nel seguente esempio simuliamo due vettori di lunghezza 100, ciascuno costruito con una sequenza di numeri interi a crescita lineare, a cui aggiungiamo rumore normalmente distribuito. In questo modo creiamo variabili associate linearmente per costruzione.
Creiamo prima un grafico a dispersione, poi calcoliamo la covarianza campionaria usando la funzione cov(). Per riprodurre esattamente gli stessi risultati, impostiamo un seed casuale di 1 e 2 per ciascuna variabile:
import numpy as np
import matplotlib.pyplot as plt
# Impostare il seed per la riproducibilità
np.random.seed(1)
x = np.arange(1, 101) + 20.0 * np.random.normal(size=100)
np.random.seed(2)
y = np.arange(1, 101) + 20.0 * np.random.normal(size=100)
# Creare il grafico
plt.scatter(x, y)
plt.show()
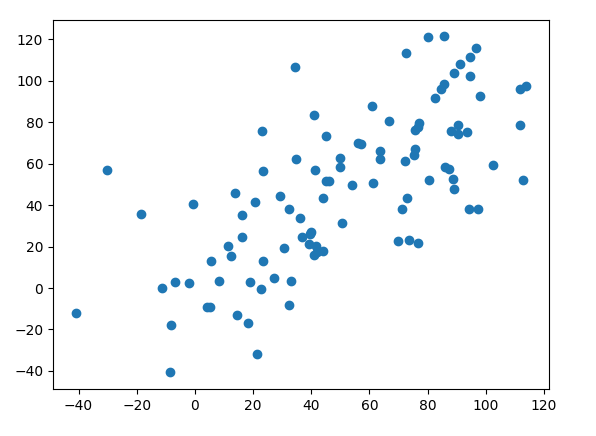
Esiste un’associazione relativamente chiara tra le due variabili.
Possiamo ora calcolare la covarianza per le due variabili come l’elemento [0,1] della matrice di covarianza quadrata:
sigma = np.cov(x,y)[0,1]
print(sigma)
La covarianza campionaria è pari a 926,1397…
Quando stimiamo l’associazione lineare tra due variabili casuali usando la covarianza, incontriamo uno svantaggio: la covarianza è una misura dimensionale. Non tiene conto della diffusione dei dati, quindi ci risulta difficile confrontare set di dati con ampie differenze di variabilità. Per questo motivo introduciamo un nuovo concetto: la correlazione.
Correlazione
Definiamo la correlazione come una misura adimensionale della relazione tra due variabili. A ogni valore della prima variabile associamo un valore della seconda seguendo una regolarità. In sostanza, calcoliamo la correlazione come la covarianza tra due variabili casuali divisa per i rispettivi spread. Usiamo il simbolo \(\rho(x, y)\) per indicare la correlazione tra due variabili:
\(\begin{eqnarray} \rho(x,y) = \frac {E[(x-\mu_x) (y-\mu_y)]} {\sigma_x \sigma_y} = \frac {\sigma(x,y)} {\sigma_x \sigma_y} \end{eqnarray}\)
Il prodotto tra i due spread al denominatore impone alla correlazione valori compresi nell’intervallo \([-1,1]\):
- Quando \(\rho(x, y) = +1\), osserviamo una relazione lineare positiva perfetta
- Quando \(\rho(x, y) = 0\), non rileviamo alcuna relazione lineare
- Quando \(\rho(x, y) = -1\), rileviamo una relazione lineare negativa perfetta
Come per la covarianza, definiamo la correlazione campionaria, indicata con \(\text{Cor}(x, y)\), nel modo seguente:
\(\begin{eqnarray} \text{Cor} (x, y) = \frac {\text{Cov (x, y)}} {\text {sd}(x) \text{sd} (y)} \end{eqnarray}\)
In questa formula, \(\text{Cov} (x, y)\) rappresenta la covarianza campionaria tra \(x\) e \(y\), mentre \(\text{sd}(x)\) indica la deviazione standard campionaria di \(x\).
Esempio: correlazione campionaria in Python
In NumPy usiamo la funzione corrcoef() per calcolare direttamente la correlazione tra due variabili. Proprio come la funzione cov(), corrcoef() restituisce una matrice, ma in questo caso si tratta di una matrice di correlazione. Per ottenere il valore che ci interessa, accediamo alla posizione [0,1] della matrice quadrata risultante.
Utilizzando gli stessi vettori \(x\) e \(y\) dell’esempio precedente, applichiamo il seguente codice Python per calcolare la correlazione campionaria:
corr = np.corrcoef(x,y)[0,1]
print(corr)
La correlazione campionaria risulta pari a 0,69839 e indica una relazione lineare positiva piuttosto forte tra i due vettori, come ci aspettavamo.
Stazionarietà nelle serie storiche
Ora che abbiamo descritto le definizioni generali di aspettativa, varianza, deviazione standard, covarianza e correlazione, possiamo applicare questi concetti ai dati delle serie temporali.
Per iniziare, introduciamo il concetto di stazionarietà, fondamentale nell’analisi delle serie temporali. Gran parte delle analisi nei dati finanziari si concentrano proprio su questo aspetto. Dopo aver chiarito la stazionarietà, affrontiamo la correlazione seriale e costruiamo alcuni grafici detti correlogrammi.
Stazionarietà della Media
Applichiamo ora le definizioni già trattate ai dati di serie temporali, partendo dalla media o aspettativa:
Media di una serie storica
La media di una serie temporale \( x_t \), \( \mu(t) \), coincide con l’aspettativa \( E(x_t) = \mu(t)\).
In questa definizione sottolineiamo due aspetti importanti:
- \( \mu = \mu(t)\), ovvero la media, in generale, dipende dal tempo.
- Ricaviamo questa aspettativa dall’insieme delle popolazioni generate dal modello di serie temporali. In particolare, non coincide con l’espressione \( (x_1 + x_2 + … + x_k) / k \) che vedremo più avanti.
Questa definizione ci aiuta quando possiamo generare molte realizzazioni del modello. Tuttavia, nella pratica disponiamo solo di una singola serie storica per ogni risorsa o situazione.
Quindi, come stimiamo la media senza avere accesso a più realizzazioni? Le opzioni sono due:
- Stimiamo la media in ogni punto usando il valore osservato.
- Scomponiamo la serie per rimuovere tendenze deterministiche o stagionalità, ottenendo una serie residua. Possiamo ipotizzare che la serie residua sia stazionaria nella media, ovvero \( \mu (t) = \mu \), un valore costante nel tempo. In tal caso, stimiamo questa media con la media campionaria \( \bar {x} = \sum ^ {n}_{t = 1} \frac {x_t} {n} \).
Stazionarietà della Media
Una serie temporale è media-stazionaria se \( \mu(t) = \mu \), cioè mantiene un valore costante nel tempo.
Stazionarietà della Varianza
Dopo aver definito l’aspettativa, la usiamo per definire la varianza. Continuiamo con l’ipotesi che la serie abbia media stazionaria. Possiamo così scrivere:
Varianza di una serie storica
La varianza \( \sigma ^ 2 (t) \) di una serie temporale con media stazionaria è data da \( \sigma ^ 2 (t) = E [(x_t – \mu) ^ 2] \).
Questa definizione estende quella della varianza per variabili casuali, ma qui \( \sigma ^ 2 (t) \) può variare nel tempo. La definizione presuppone che \( \mu \) non dipenda dal tempo.
Ci accorgiamo subito che, se la varianza cambia nel tempo, stimarla da una singola serie diventa difficile. Anche qui, la presenza di \( E (..) \) richiede un insieme di serie temporali, ma quasi sempre ne abbiamo solo una!
Semplifichiamo nuovamente la situazione: supponiamo una varianza costante della popolazione, \( \sigma ^ 2 \), indipendente dal tempo. A questo punto, possiamo stimare il valore usando la varianza campionaria:
\(\begin{eqnarray} \text {Var (x)} = \frac {\sum (x_t – \bar {x}) ^ 2} {n-1} \end{eqnarray}\)
Affinché questa formula funzioni, dobbiamo stimare correttamente la media campionaria \( \bar {x} \). Inoltre, come per la covarianza campionaria, utilizziamo \( n-1 \) al denominatore per ottenere uno stimatore imparziale.
Stazionarietà della varianza
Una serie temporale è stazionaria nella varianza se \( \sigma ^ 2 (t) = \sigma ^ 2 \), ovvero mantiene varianza costante nel tempo.
A questo punto, dobbiamo prestare attenzione! Le osservazioni sequenziali possono essere correlate nelle serie temporali. Questo fenomeno può influenzare la stima della varianza, portando a una sovrastima o sottostima della varianza reale.
Il problema diventa serio quando disponiamo di pochi dati. In una serie con alta correlazione, le osservazioni risultano molto simili e introducono un bias.
Nella pratica, soprattutto nella finanza ad alta frequenza, lavoriamo con grandi quantità di dati. Tuttavia, spesso non possiamo assumere che le serie finanziarie siano veramente stazionarie nella media o stazionarie nella varianza.
Nel prosieguo della lezione e nei modelli che svilupperemo, affronteremo questi limiti per migliorare previsioni e simulazioni.
Siamo ora pronti per applicare le definizioni di media e varianza alla correlazione seriale.
Correlazione seriale
Comprendere la correlazione seriale significa verificare in che modo le osservazioni sequenziali di una serie temporale si influenzano tra loro. Quando identifichiamo una struttura in queste osservazioni, possiamo migliorare le nostre previsioni e aumentare l’accuratezza delle simulazioni. Questo ci consente di ottenere maggiore redditività nelle strategie di trading o di affinare gli approcci nella gestione del rischio.
Procediamo con una nuova definizione. Supponiamo, come già fatto, di analizzare una serie temporale stazionaria nella media e stazionaria nella varianza. In questo contesto, possiamo definire la stazionarietà del secondo ordine:
Stazionarietà di secondo ordine
Consideriamo una serie temporale stazionaria di secondo ordine quando la correlazione tra le osservazioni sequenziali dipende esclusivamente dal ritardo (lag), ovvero il numero di periodi che separa ogni osservazione successiva.
A questo punto, definiamo la covarianza seriale e la correlazione seriale!
Autocovarianza di una serie storica
Se analizziamo un modello di serie temporale stazionario di secondo ordine, definiamo la covarianza seriale, o autocovarianza, con ritardo \(k\) come: \(C_k = E[(x_t – \mu)(x_{t+k} – \mu)]\).
L’autocovarianza \(C_k\) non varia nel tempo perché dipende da un’aspettativa \(E(..)\), che, come abbiamo visto, si calcola sull’intera popolazione delle possibili serie temporali. Di conseguenza, resta costante per tutti i valori di \(t\).
Da questa definizione otteniamo la correlazione seriale o autocorrelazione, semplicemente dividendo per il quadrato della deviazione standard della serie. Possiamo farlo perché la serie temporale risulta stazionaria nella varianza e quindi \(\sigma^2(t) = \sigma^2\):
Autocorrelazione di una serie storica
Definiamo la correlazione seriale, o autocorrelazione, con ritardo \(k\), \(\rho_k\), come il rapporto tra l’autocovarianza della serie e la varianza: \(\rho_k = \frac{C_k}{\sigma^2}\).
Osserviamo che \(\rho_0 = \frac{C_0}{\sigma^2} = \frac{E[(x_t – \mu)^2]}{\sigma^2} = \frac{\sigma^2}{\sigma^2} = 1\). Quindi, il primo ritardo con \(k = 0\) fornisce sempre un valore pari a uno.
Come nel caso delle definizioni di covarianza e correlazione, anche per autocovarianza e autocorrelazione possiamo calcolare le versioni campionarie. Per distinguerle dai valori della popolazione, indichiamo l’autocovarianza campionaria con \(c\) minuscola rispetto alla \(C\) maiuscola.
La funzione di autocovarianza campionaria \(c_k\) si calcola così:
\(\begin{eqnarray} c_k = \frac{1}{n} \sum_{t=1}^{n-k} (x_t – \bar{x})(x_{t+k} – \bar{x}) \end{eqnarray}\)
La funzione di autocorrelazione campionaria \(r_k\) si ottiene tramite:
\(\begin{eqnarray} r_k = \frac{c_k}{c_0} \end{eqnarray}\)
Una volta definita la funzione di autocorrelazione campionaria, possiamo costruire e interpretare il correlogramma, uno strumento fondamentale per l’analisi delle serie temporali.
Il Correlogramma
Chiamiamo correlogramma il grafico della funzione di autocorrelazione per diversi valori di ritardo, \(k = 0,1,\dots,n\). Questo grafico ci permette di visualizzare la struttura di correlazione seriale per ciascun lag.
Utilizziamo i correlogrammi soprattutto per identificare autocorrelazioni residue dopo aver rimosso trend deterministici ed effetti stagionali.
Dopo aver adattato un modello di serie temporale, analizziamo il correlogramma per verificare la bontà dell’adattamento oppure per individuare la necessità di perfezionarlo e rimuovere eventuali autocorrelazioni residue.
Ecco un esempio di correlogramma realizzato in Python con la funzione acf, utilizzando una sequenza di variabili casuali normalmente distribuite. Di seguito riportiamo il codice Python completo:
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
s = np.random.normal(size=100)
acf_coef = acf(s)
plot_acf(acf_coef, lags=20)
plt.show()
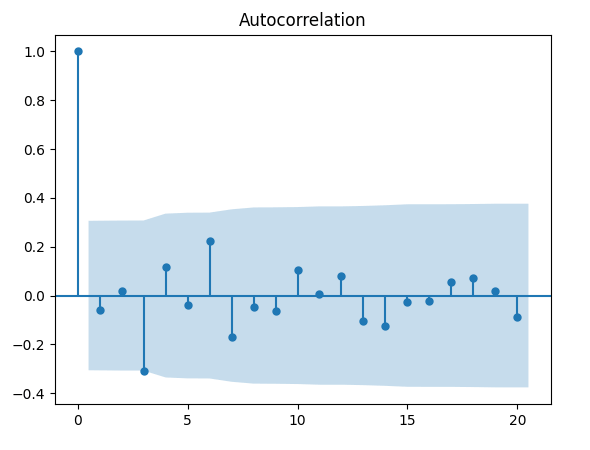
Da notare le caratteristiche specifiche del grafico del correlogramma:
- In primo luogo, poiché la correlazione campionaria del ritardo \( k = 0 \) è data da \( r_0 = \frac {c_0} {c_0} = 1 \), nel grafico avremo sempre una linea di altezza uguale ad 1 per il ritardo \( k = 0 \). In effetti, questo ci fornisce un punto di riferimento su cui giudicare le restanti autocorrelazioni per i ritardi successivi. Si noti inoltre che l’ACF dell’asse y è adimensionale, poiché la correlazione è essa stessa adimensionale.
- L’area blu rappresenta il confine per cui se i valori non rientrano in questa area, si ha evidenza che la nostra correlazione al lag \( k \), \( r_k \), sia uguale a zero al livello del 5%. Tuttavia dobbiamo fare attenzione perché dovremmo aspettarci che il 5% di questi ritardi superi comunque questi valori! Inoltre stiamo visualizzando i valori correlati e quindi se un ritardo cade al di fuori di questi limiti, è più probabile che lo facciano anche i prossimi valori sequenziali. In pratica stiamo cercando ritardi che possano avere qualche motivo di fondo per superare il livello del 5%. Ad esempio, in una serie temporale di materie prime potremmo vedere effetti imprevisti della stagionalità a determinati ritardi (possibilmente intervalli mensili, trimestrali o annuali).
Ecco un paio di esempi di correlogrammi per sequenze di dati.
Esempio 1 – Trend lineare fisso
Il seguente codice Python genera una sequenza di numeri interi da 1 a 100 e quindi traccia l’autocorrelazione:
w = np.arange(1, 100)
acf_coef = acf(w, nlags=100)
plot_acf(acf_coef, lags=20)
plt.show()
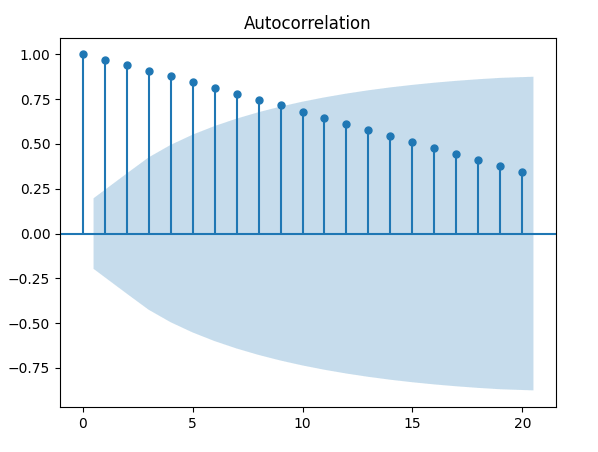
Da notare come il grafico ACF diminuisce in modo quasi lineare all’aumentare dei ritardi. Quindi un correlogramma di questo tipo è una chiara indicazione della presenza di un trend.
Esempio 2 – Sequenza ripetuta
Il seguente codice Python genera una sequenza ripetuta di numeri con periodo \( p = 10 \) e quindi traccia l’autocorrelazione:
a = np.arange(1,11)
s = []
for i in range (0,10):
for j in range (0,10):
s.append(a[j])
acf_coef = acf(s)
plot_acf(acf_coef, lags=20)
plt.show()
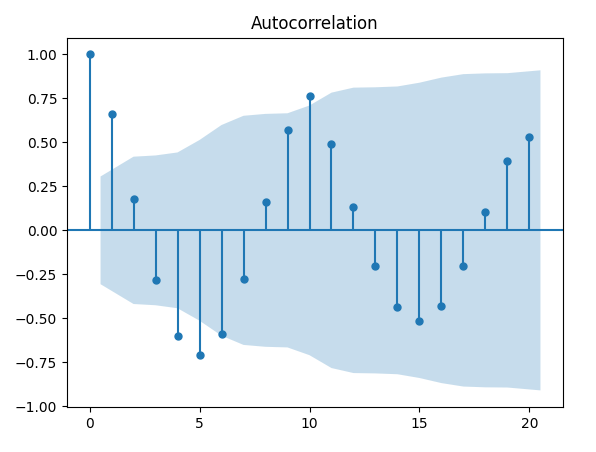
Osserviamo picchi significativi ai ritardi 10 e 20. Questo risultato ci appare logico, dato che le sequenze si ripetono con un periodo di 10. Notiamo anche una correlazione seriale negativa, esattamente di -0,5, per i ritardi 5 e 15.
Questa caratteristica rispecchia il comportamento tipico delle serie temporali stagionali. Quando individuiamo una simile struttura in un correlogramma, comprendiamo che la stagionalità o gli effetti periodici non sono stati ancora considerati completamente all’interno del modello.
Conclusioni
Dopo aver descritto in modo approfondito la correlazione seriale, l’autocorrelazione e i correlogrammi, nelle prossime lezioni introdurremo i modelli lineari e avvieremo il processo di previsione.
Anche se i modelli lineari non rappresentano lo stato dell’arte nell’analisi delle serie temporali, scegliamo di sviluppare la teoria a partire dai casi più semplici. Solo così potremo applicarla in modo efficace ai modelli non lineari più avanzati oggi disponibili.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

