Nelle prossime lezioni descriviamo il modello autoregressivo (AR) di ordine p, che insieme al modello a media mobile (MA) di ordine q e il modello autoregressivo a media mobile (ARMA) di ordine misto (p, q). Questi modelli ci permettono di catturare o “spiegare” la correlazione seriale all’interno di uno strumento e ci offrono un mezzo utile per le previsioni dei prezzi futuri.
Nell’ultima lezione abbiamo analizzato il White Noise e Random Walk come modelli di base per le serie temporali di strumenti finanziari. Abbiamo osservato che in certi casi il modello di Random Walk non riesce a cogliere appieno il comportamento di autocorrelazione dello strumento. Per questo motivo utilizziamo modelli più sofisticati.
Sappiamo però che le serie temporali finanziarie presentano una caratteristica chiamata clustering di volatilità: la volatilità dello strumento varia nel tempo. Questo comportamento, che definiamo eteroschedasticità condizionale, non viene gestito dai modelli AR, MA e ARMA, poiché non considerano questa dinamica. Per produrre previsioni accurate, dobbiamo quindi adottare un modello più avanzato.
Tra questi modelli troviamo il modello Autoregressivo a Varianza Condizionata (ARCH) e il modello Generalizzato ARCH (GARCH), oltre a molte varianti. Il modello GARCH ricopre un ruolo centrale nella finanza quantitativa e lo utilizziamo spesso per simulare serie temporali finanziarie e stimare il rischio.
Come in tutte le lezioni di TradingQuant, costruiamo i modelli partendo dalle versioni più semplici per comprendere come ogni variante influenzi la nostra capacità predittiva. Anche se il modello autoregressivo (AR) di ordine p, e gli altri modelli MA e ARMA risultano relativamente semplici, costituiscono le fondamenta di modelli più complessi come l’Autoregressive Integrated Moving Average (ARIMA) e della famiglia GARCH. Per questo motivo li studiamo in dettaglio.
Una delle nostre prime strategie di trading nella serie di lezioni dedicate alle serie temporali prevede la combinazione di ARIMA e GARCH per prevedere i prezzi con n-periodi di anticipo. Prima di applicare questa combinazione a una strategia reale, esploreremo in dettaglio sia ARIMA che GARCH.
Introduzione
In questa lezione introduciamo alcuni concetti fondamentali delle serie temporali che ritroveremo nei modelli successivi, in particolare la stazionarietà rigorosa e il criterio dell’informazione di Akaike (AIC). Dopo averli introdotti, seguiamo lo schema tradizionale che adottiamo nello studio dei modelli di serie temporali:- Razionale – Spieghiamo perché ci interessa uno specifico modello. Quali effetti riesce a catturare? Cosa otteniamo (o perdiamo) aggiungendo complessità?
- Definizione – Forniamo la definizione matematica completa e la relativa notazione per evitare ambiguità.
- Proprietà del secondo ordine – Analizziamo, e a volte deriviamo, le proprietà di secondo ordine del modello: media, varianza e funzione di autocorrelazione.
- Correlogramma – Tracciamo il correlogramma di una realizzazione del modello sfruttando le proprietà di secondo ordine per visualizzarne il comportamento.
- Simulazione – Simuliamo le realizzazioni del modello e lo adattiamo a tali simulazioni per assicurarci che l’implementazione sia accurata e comprensibile.
- Dati finanziari reali – Adattiamo il modello a dati finanziari reali e analizziamo il correlogramma dei residui per valutare se il modello gestisce correttamente la correlazione seriale della serie originale.
- Pronostico – Eseguiamo n-step ahead forecasts per specifiche realizzazioni del modello, al fine di generare segnali di trading.
Stazionarietà Rigorosa
Abbiamo già definito la stazionarietà nella lezione sulla correlazione seriale. Ora, poiché analizziamo molte serie finanziarie con frequenze diverse, ci assicuriamo che i modelli tengano conto della volatilità che cambia nel tempo. In particolare, consideriamo la loro eteroschedasticità. Affrontiamo questo problema quando adattiamo specifici modelli alle serie storiche. In generale, non possiamo ignorare la correlazione seriale nei residui se non teniamo conto dell’eteroschedasticità. Questo ci riporta al concetto di stazionarietà. Per definizione, una serie presenta varianza non stazionaria se la sua volatilità cambia nel tempo. Per questo motivo introduciamo una definizione più rigorosa: la stazionarietà rigorosa.Serie rigorosamente stazionaria Definiamo una serie storica, \(\{ x_t \}\), rigorosamente stazionaria se la distribuzione congiunta degli elementi \(x_{t_1},\ldots,x_{t_n}\) coincide con quella di \(x_{t_{1}+m},\ldots,x_{t_{n}+m}\), per ogni valore di m.Possiamo interpretare questa definizione dicendo che la distribuzione della serie temporale resta invariata per qualsiasi spostamento arbitrario nel tempo. In particolare, una serie rigorosamente stazionaria mantiene costanti nel tempo la media, la varianza e l’autocovarianza tra \(x_t\) e \(x_s\), che dipende soltanto da \(|t-s|\). Riprenderemo l’argomento delle serie rigorosamente stazionarie nelle prossime lezioni.
Criterio di informazione di Akaike (AIC)
Nelle lezioni precedenti abbiamo anticipato la necessità di confrontare diversi modelli per scegliere il “migliore”. Questo approccio vale sia per l’analisi delle serie temporali, sia per il machine learning e più in generale per la statistica. Al momento adottiamo due criteri principali: l’Akaike Information Criterion (AIC) e il Bayesian Information Criterion, che descritto nel corso sulla statistica bayesiana. Introduciamo brevemente l’AIC, che utilizziamo nella nelle prossime lezioni. L’AIC rappresenta uno strumento utile per selezionare i modelli. Quando disponiamo di una serie di modelli statistici, comprese le serie temporali, l’AIC ci permette di stimare la “qualità” di ciascun modello rispetto agli altri disponibili. Basandoci sulla teoria dell’informazione, un argomento affascinante e complesso, bilanciamo la complessità del modello (ovvero il numero di parametri) con la sua capacità di adattarsi ai dati. Ecco la definizione:Criterio informativo di Akaike Supponiamo di utilizzare la funzione di verosimiglianza per un modello statistico con \(k\) parametri, e che \(L\) rappresenti il valore che massimizza la verosimiglianza. Allora il criterio informativo di Akaike si esprime come: \(\begin{eqnarray}AIC = -2 \text{log} (L) + 2k \end{eqnarray}\)Scegliamo come “migliore” il modello che presenta l’AIC più basso tra tutti. Notiamo che l’AIC cresce con il numero di parametri k, ma diminuisce quando la log-verosimiglianza negativa aumenta. In sostanza, penalizziamo i modelli che fanno overfitting. Nel seguito, descriviamo i modelli AR, MA e ARMA con ordini diversi. Nella prossima lezione presentiamo un metodo basato sull’AIC per selezionare il miglior modello ARMA in base a un determinato set di dati.
Modello autoregressivo (AR) di ordine p
Il primo modello che analizziamo, base di questa lezione, è il modello autoregressivo (AR) di ordine p, comunemente abbreviato in AR(p).Fondamento logico
Nella lezione precedente abbiamo descritto il random walk, dove ogni termine \(x_t\) dipende unicamente dal termine precedente \(x_{t-1}\) e da un termine stocastico di rumore bianco \(w_t\): \(\begin{eqnarray} x_t = x_{t-1} + w_t \end{eqnarray}\) Abbiamo esteso il modello di passeggiata casuale includendo termini più arretrati nel tempo. La struttura del modello rimane lineare, cioè dipende linearmente dai valori passati con relativi coefficienti. Da qui nasce il termine “regressivo” in “autoregressivo”: si tratta, infatti, di una regressione in cui utilizziamo i termini precedenti come predittori.Modello autoregressivo di ordine p Un modello di serie storica, \(\{ x_t \}\), è un modello autoregressivo di ordine p, AR(p), se:Notiamo subito che una passeggiata casuale corrisponde a un AR(1) con \(\alpha_1\) uguale a uno. Come anticipato, il modello autoregressivo rappresenta un’estensione naturale del random walk: tutto torna! Prevediamo facilmente con il modello AR(p): una volta stimati i coefficienti \(\alpha_i\), otteniamo la previsione:\(\begin{eqnarray} x_t &=& \alpha_1 x_{t-1} + \ldots + \alpha_p x_{t-p} + w_t \\ &=& \sum_{i=1}^p \alpha_i x_{t-i} + w_t \end{eqnarray}\)
Dove \(\{ w_t \}\) rappresenta il rumore bianco e \(\alpha_i \in \mathbb{R}\), con \(\alpha_p \neq 0\) per definire un processo AR di ordine p. Se applichiamo l’operatore di spostamento all’indietro, B (vedi lezione precedente), riscriviamo il modello come funzione θ di B:\(\begin{eqnarray} \theta_p ({\bf B}) x_t = (1 – \alpha_1 {\bf B} – \alpha_2 {\bf B}^2 – \ldots – \alpha_p {\bf B}) x_t = w_t \end{eqnarray}\)
\(\begin{eqnarray} \hat{x}_t = \alpha_1 x_{t-1} + \ldots + \alpha_p x_{t-p} \end{eqnarray}\)
Possiamo poi estendere le previsioni a n-passi avanti, producendo \(\hat{x}_t\), \(\hat{x}_{t+1}\), \(\hat{x}_{t+2}\) e così via fino a \(\hat{x}_{t+n}\). Nelle prossime lezioni descriveremo i modelli ARMA e utilizzeremo una funzione Python per generare previsioni, insieme alle bande di confidenza, utili per produrre segnali di trading.Stazionarietà per processi autoregressivi
Tra gli aspetti più critici del modello AR(p) troviamo la stazionarietà, che non sempre risulta garantita. La dipendenza dalla stazionarietà deriva dai parametri del modello. Per capire se un processo AR(p) è stazionario, risolviamo la sua equazione caratteristica, che otteniamo riscrivendo il modello autoregressivo in forma di spostamento all’indietro, impostandolo a zero:\(\begin{eqnarray} \theta_p({\bf B}) = 0 \end{eqnarray}\)
Risolvendo per B, otteniamo le radici dell’equazione. Per garantire la stazionarietà del processo, dobbiamo verificare che i valori assoluti di tutte le radici siano maggiori di uno. Questa condizione si rivela utile per testare rapidamente la stazionarietà del processo AR(p). Osserviamo ora alcuni esempi per chiarire meglio il concetto:- Random Walk – Nel processo AR(1) con \(\alpha_1 = 1\) otteniamo l’equazione \(\theta = 1 – {\bf B}\). La radice \({\bf B} = 1\) ci indica che la serie non è stazionaria.
- AR(1) – Scegliendo \(\alpha_1 = \frac{1}{4}\), otteniamo \(x_t = \frac{1}{4} x_{t-1} + w_t\), con equazione caratteristica \(1 – \frac{1}{4} {\bf B} = 0\), che ha radice \({\bf B} = 4 > 1\): dunque, il processo è stazionario.
- AR(2) – Impostando \(\alpha_1 = \alpha_2 = \frac{1}{2}\), otteniamo \(x_t = \frac{1}{2} x_{t-1} + \frac{1}{2} x_{t-2} + w_t\), con equazione \(-\frac{1}{2}({\bf B-1})({\bf B+2}) = 0\). Le radici risultano \({\bf B} = 1, -2\). La presenza della radice unitaria indica una serie non stazionaria. Tuttavia, altri processi AR(2) risultano stazionari.
Proprietà del secondo ordine
La media di un processo AR(p) è pari a zero. Le autocovarianze e autocorrelazioni seguono invece relazioni ricorsive, chiamate equazioni di Yule-Walker. Ecco le proprietà fondamentali:\(\begin{eqnarray} \mu_x = E(x_t) = 0 \end{eqnarray}\)\(\begin{eqnarray} \gamma_k = \sum_{i=1}^p \alpha_i \gamma_{k-i}, \enspace k > 0 \end{eqnarray}\) \(\begin{eqnarray} \rho_k = \sum_{i=1}^p \alpha_i \rho_{k-i}, \enspace k > 0 \end{eqnarray}\)
Dobbiamo conoscere i valori dei parametri \(\alpha_i\) per calcolare le autocorrelazioni. Ora che abbiamo definito le proprietà del secondo ordine, possiamo simulare processi AR(p) di diversi ordini e tracciare i rispettivi correlogrammi.Simulazioni e Correlogrammi
AR(1)
Iniziamo con un processo AR(1). Questo è simile a una passeggiata casuale, tranne che \(\alpha_1\) non deve eguagliare l’unità. Il nostro modello avrà \(\alpha_1 = 0.6\). Il codice Python per la creazione di questa simulazione è il seguente:
import numpy as np
from statsmodels.tsa.arima_process import ArmaProcess
# AR parameter = +0.6
ar1 = np.array([1, -0.6])
ma1 = np.array([1])
AR_object1 = ArmaProcess(ar1, ma1)
simulated_data_1 = AR_object1.generate_sample(nsample=1000)
Possiamo quindi tracciare il grafico di questo modello e del relativo correlogramma.
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import acf
# Plot AR model
plt.plot(simulated_data_1)
acf_coef = acf(simulated_data_1)
plot_acf(acf_coef, lags=30)
plt.show()
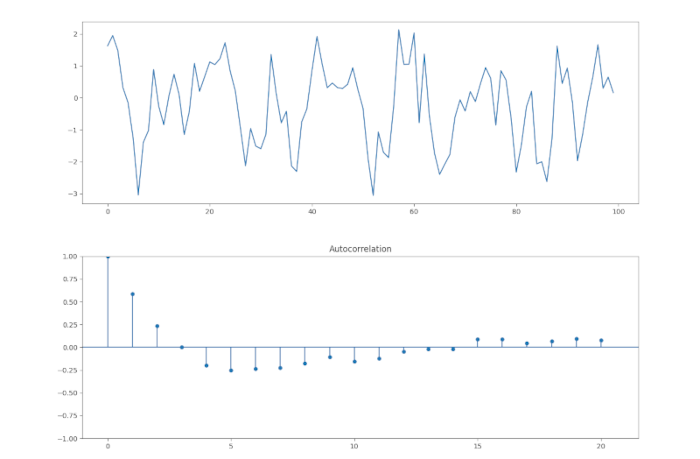
Proviamo ora ad adattare un processo AR(p) ai dati simulati che abbiamo appena generato, per vedere se possiamo recuperare i parametri sottostanti. Abbiamo eseguito una procedura simile nella lezione relativa White Noise e Random Walks.
Il pacchetto stasmodels di Python fornisce i metodi per adattare i modelli autoregressivi. Possiamo usare questi metodi per fornirci le stime dei parametri per i \(\alpha_i\), che possiamo quindi utilizzare per formare intervalli di confidenza.
Usiamo il comando ARMA per adattare un modello autoregressivo al nostro processo AR(1) simulato, utilizzando la stima di massima verosimiglianza (MLE) come procedura di adattamento.
from statsmodels.tsa.arima_model import ARMA
# Fit an AR(1) model to the first simulated data
mod = ARMA(simulated_data_1, order=(1, 0))
res = mod.fit()
# Print out summary information on the fit
print(res.summary())
# Print out the estimate for the constant and for alpha
print("When the true alpha=0.9, the estimate of alpha (and the constant) are:")
print(res.params)
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: ARMA(1, 0) Log Likelihood -145.403
Method: css-mle S.D. of innovations 1.033
Date: 27 Sep 2017 AIC 296.807
Time: 17:01:04 BIC 304.622
Sample: 0 HQIC 299.970
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0644 0.272 0.237 0.813 -0.468 0.597
ar.L1.y 0.6261 0.077 8.155 0.000 0.476 0.777
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.5973 +0.0000j 1.5973 0.0000
-----------------------------------------------------------------------------
When the true parameter=0.6, the estimate of parameter (and the constant) are:
[0.06443423 0.62607235]
La procedura MLE ha prodotto un valore stimato \(\hat{\alpha_1} = 0.626\), che è leggermente superiore al valore reale di \(\).
Inoltre il report utilizza l’errore standard (con la varianza asintotica) per costruire intervalli di confidenza del 95% attorno ai parametri sottostanti. Quindi si evidenzia che il vero parametro rientra nell’intervallo di confidenza del 95%, come ci si aspetterebbe dal fatto che abbiamo generato la realizzazione dal modello in modo specifico.
Vediamo lo stesso approccio considerando \(\alpha_1 =-0.6\).
# AR parameter = -0.6
ar2 = np.array([1, +0.6])
ma2 = np.array([1])
AR_object2 = ArmaProcess(ar2, ma2)
simulated_data_2 = AR_object2.generate_sample(nsample=100)
# Plot AR model
plt.plot(simulated_data_2)
plot_acf(simulated_data_2, alpha=1, lags=20)
plt.show()
Anche in questo caso possiamo adattare un modello AR(p) usando il metodo
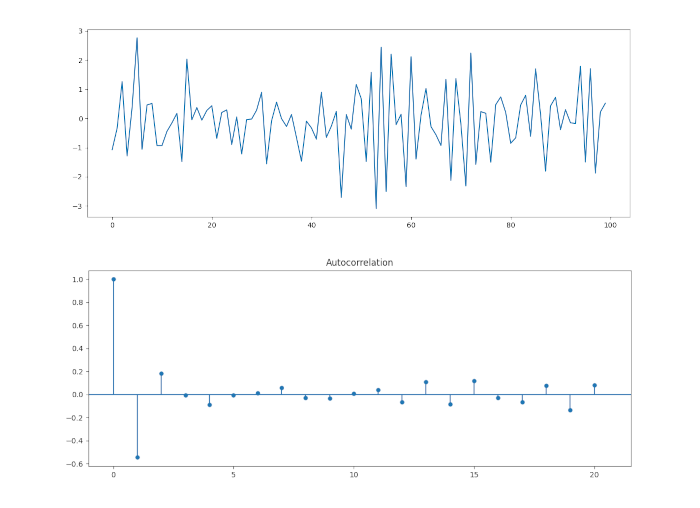
ARMA e otteniamo il seguente report:
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: ARMA(1, 0) Log Likelihood -141.901
Method: css-mle S.D. of innovations 0.997
Date: 27 Sep 2017 AIC 289.801
Time: 17:20:25 BIC 297.617
Sample: 0 HQIC 292.964
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0281 0.061 0.459 0.647 -0.092 0.148
ar.L1.y -0.6389 0.076 -8.454 0.000 -0.787 -0.491
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.5652 +0.0000j 1.5652 0.5000
-----------------------------------------------------------------------------
When the true parameter=-0.6, the estimate of parameter (and the constant) are:
[ 0.02807516 -0.63889385]
Ancora una volta abbiamo il corretto ordine del modello, con una valore stimato \(\hat{\alpha_1}=-0.6389\) di \(\hat{\alpha_1}=-0.6\). Vediamo anche che il parametro rientra ancora una volta nell’intervallo di confidenza del 95%.
AR(2)
Aggiungiamo un po’ più di complessità ai nostri processi autoregressivi simulando un modello di ordine 2. In particolare, impostiamo \(\alpha_1=0.666\) e \(\alpha_2 = -0.333\). Ecco il codice completo per simulare e tracciare le realizzazioni, così come il correlogramma per una serie del genere:
# AR(2) parameter = 0.666 and -0.333
ar_2o = np.array([1, -0.666, 0.333])
ma_2o = np.array([1])
AR_object_2o = ArmaProcess(ar_2o, ma_2o)
simulated_data_2o = AR_object_2o.generate_sample(nsample=100)
# Plot AR model
plt.plot(simulated_data_2o)
plot_acf(simulated_data_2o, alpha=1, lags=20)
plt.show()
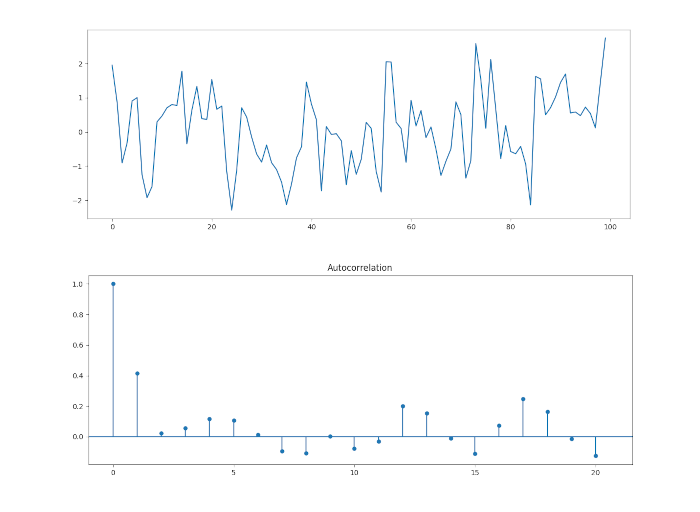
Come per gli esempi precedenti, notiamo che il correlogramma differisce significativamente da quello del rumore bianco, come ci si aspetterebbe. Ci sono picchi statisticamente significativi.
Ancora una volta, usiamo il metodo ARMA per adattare un modello AR(p) alla nostra realizzazione AR(2) sottostante. La procedura è simile a quella per l’adattamento AR(1):
# Fit an AR(2) model to the first simulated data
mod = ARMA(simulated_data_2o, order=(2, 0, 0))
res = mod.fit()
# Print out summary information on the fit
print(res.summary())
# Print out the estimate for the constant and for phi
print("When the true parameters are 0.666 and -0.333, the estimate of parameters (and the constant) are:")
print(res.params)
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: ARMA(2, 0) Log Likelihood -137.754
Method: css-mle S.D. of innovations 0.957
Date: 27 Sep 2017 AIC 283.508
Time: 17:49:19 BIC 293.929
Sample: 0 HQIC 287.726
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.2259 0.149 1.519 0.132 -0.066 0.517
ar.L1.y 0.6841 0.094 7.286 0.000 0.500 0.868
ar.L2.y -0.3274 0.094 -3.502 0.001 -0.511 -0.144
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0446 -1.4010j 1.7475 -0.1480
AR.2 1.0446 +1.4010j 1.7475 0.1480
-----------------------------------------------------------------------------
When the true parameters are 0.666 and -0.333, the estimate of parameters (and the constant) are:
[ 0.22589332 0.68412184 -0.32744997]
Notiamo che l’ordine corretto è stato recuperato e le stime dei parametri \(\hat{\alpha_1}=0.6841\) e \(\hat{\alpha_2}=-0.3274\) non sono troppo lontani dai valori dei parametri veri \(\hat{\alpha_1}=0.666\) e \(\hat{\alpha_2}=-0.333\).
Come vedremo negli articoli successivi, i modelli AR(p) sono semplicemente modelli ARIMA(p, 0, 0), e quindi un modello AR è un caso speciale del modello ARIMA senza componenti di media mobile (MA).
Questo motiva la prossima serie di modelli, vale a dire la media mobile MA(q) e la media mobile autoregressiva ARMA(p, q). Descriviamo entrambi questi aspetti nella parte 2 di questo articolo. Come abbiamo ripetutamente menzionato, questi alla fine ci porteranno alla famiglia di modelli ARIMA e GARCH, che forniranno entrambi un adattamento molto migliore alla complessità della correlazione seriale delle serie temporali di dati finanziari.
Questo ci consentirà di migliorare significativamente le nostre previsioni e, in definitiva, di produrre strategie più redditizie.