In questa lezione introduciamo il concetto di cointegrazione delle serie temporali, che ci permette di verificare se possiamo costruire una coppia di asset mean-reverting, cioè con ritorno medio. Presentiamo la teoria delle serie temporali relativa alla cointegrazione e poi la applichiamo a strategie di trading reali utilizzando un framework di backtesting open source.
Descriviamo il ritorno alla media nel tradizionale contesto del “pairs-trading”. Introduciamo il concetto di stazionarietà di una combinazione lineare di asset, per poi definire la cointegrazione e i test di radice unitaria. Dopo aver delineato questi test, simuliamo varie serie temporali con Python e applichiamo i test per analizzare la cointegrazione delle serie temporali.
Strategie di trading di reversione media
L’idea centrale del pairs-trading mean-reverting consiste nell’aprire contemporaneamente posizioni long e short su due asset diversi. Questi asset devono condividere fattori comuni che ne influenzano i movimenti. Un esempio nel settore azionario potrebbe essere una posizione long su McDonald’s (NYSE:MCD) e short su Burger King (NYSE:BKW – prima della fusione con Tim Horton’s).
La logica di questa strategia risiede nell’elevata probabilità che i prezzi dei due asset ritornino all’equilibrio nel lungo termine, a causa di fattori di mercato condivisi legati alla produzione e consumo di hamburger. Un evento isolato, come un’interruzione della catena di approvvigionamento che colpisce solo McDonald’s, può generare una temporanea dislocazione nei prezzi relativi. In quel momento, un’operazione long-short può risultare profittevole se i prezzi tornano all’equilibrio una volta risolta l’interruzione. Questo rappresenta l’essenza del classico pairs-trading.
Come quants, puntiamo a fare trading su asset mean-reverting non solo in coppia, ma anche in panieri di titoli connessi tra loro.
Per farlo, costruiamo un solido modello matematico che ci consente di individuare coppie o panieri di titoli che seguono questo comportamento. Qui entra in gioco la cointegrazione delle serie temporali.
Partiamo da una coppia di serie temporali non stazionarie, come i prezzi simil-random walk di MCD e BKW, e costruiamo una combinazione lineare di esse per ottenere una serie stazionaria, con media e varianza costanti.
Questa nuova serie stazionaria può deviare dalla media nel breve termine, ma tende sempre a ritornarvi nel tempo. Possiamo sfruttare questo comportamento nelle nostre strategie di trading, aprendo posizioni long/short al momento opportuno e puntando al ritorno della serie alla media.
Le strategie di mean-reverting ci permettono di creare serie temporali stazionarie “sintetiche” su una vasta gamma di strumenti finanziari. Non ci limitiamo certo alle azioni tradizionali. Ad esempio, possiamo usare gli ETF che replicano i prezzi delle materie prime, come il petrolio, o panieri di aziende energetiche. La cointegrazione delle serie temporali apre molte opportunità per identificare questi sistemi di mean-reverting.
Prima di approfondire i meccanismi delle strategie di trading, che tratteremo in lezioni successive, impariamo a identificare statisticamente le serie cointegrate. A questo scopo, utilizziamo le tecniche dell’analisi delle serie temporali, continuando a usare Python come nei corsi di finanza quantitativa.
Cointegrazione delle serie temporali
Dopo aver motivato la necessità di un approccio quantitativo per fare mean-reversion trading, definiamo il concetto di cointegrazione. Consideriamo due serie temporali non stazionarie: se esiste una combinazione lineare di queste serie che genera una nuova serie stazionaria, allora le due serie sono cointegrate.
Cointegrazione
Date due serie temporali non stazionarie, cona, b ∈ ℝ, se la serie combinataa xₜ + b yₜè stazionaria, allora{xₜ}e{yₜ}sono cointegrate.
Anche se questa definizione è chiara, non ci fornisce direttamente i valori di a e b né ci dice come verificare se la combinazione è stazionaria. Per questo utilizziamo i test per le radici unitarie, strumenti fondamentali nell’analisi della cointegrazione delle serie temporali.
Test di radice unitaria
Nella lezione precedente sui modelli autoregressivi AR(p) abbiamo spiegato il ruolo dell’equazione caratteristica. Abbiamo mostrato che si tratta di un semplice modello autoregressivo annullato, scritto in forma retrospettiva. Risolviamo questa equazione per ottenere un insieme di radici.
Affinché il modello risulti stazionario, tutte le radici devono superare l’unità. Se una radice vale uno — ovvero si presenta una radice unitaria — il modello AR(p) non è stazionario. Le passeggiate casuali rappresentano processi AR(1) con radici unitarie, quindi risultano non stazionarie.
Per verificare se una serie temporale è stazionaria, costruiamo un test di ipotesi statistica che identifichi la presenza di una radice unitaria all’interno del campione.
Analizziamo tre test differenti: Augmented Dickey-Fuller (ADF), Phillips-Perron e Phillips-Ouliaris. Anche se partono da ipotesi diverse, tutti mirano a verificare la stazionarietà delle serie temporali nel campione.
Ora descriviamo brevemente i metodi utilizzati da ciascun test.
Test di Dickey-Fuller aumentato
Dickey e Fuller [2] hanno proposto un test per individuare una radice unitaria. Il test considera una serie \(z_t = \alpha z_{t-1} + w_t\), dove \(w_t\) rappresenta rumore bianco. L’ipotesi nulla assume \(\alpha = 1\), mentre l’alternativa è \(\alpha < 1\).
Successivamente, Said e Dickey [6] hanno esteso il test originale in quello Augmented Dickey-Fuller (ADF), trasformando \(z_t\) da un modello AR(1) a uno AR(p). Abbiamo illustrato questo test in una lezione dove, tramite Python, calcoliamo il test ADF. In questa lezione applichiamo lo stesso metodo.
Test di Phillips-Perron
Nel test ADF adottiamo un modello AR(p) per stimare le autocorrelazioni superiori. Con il test Phillips-Perron [5], invece, non facciamo alcuna approssimazione del tipo AR(p). Applichiamo un metodo non parametrico di smoothing con kernel al processo \(w_t\), per considerare l’autocorrelazione e l’eteroscedasticità non definite.
Test di Phillips-Ouliaris
Il test di Phillips-Ouliaris [4] si distingue dagli altri due perché verifica l’esistenza di cointegrazione nei residui tra due serie. Poiché il test ADF applicato ai residui cointegranti stimati non segue la distribuzione Dickey-Fuller sotto l’ipotesi nulla, utilizziamo le distribuzioni Phillips-Ouliaris per una valutazione più appropriata della cointegrazione delle serie temporali.
Difficoltà con gli Unit Root Test
Anche se i test ADF e Phillips-Perron risultano asintoticamente equivalenti, su campioni finiti forniscono spesso risultati differenti [7]. Ciò avviene perché trattano in modo diverso autocorrelazione ed eteroscedasticità. Dobbiamo chiarire bene quali ipotesi intendiamo testare e non applicare questi metodi in modo arbitrario.
Inoltre, i test di radice unitaria non riescono a distinguere con efficacia tra processi altamente persistenti e non stazionari. Dobbiamo prestare attenzione quando li applichiamo a serie temporali finanziarie, soprattutto se la relazione modellata (come il ritorno alla media tra due asset) cambia per via di mutamenti strutturali o di regime.
Simulazione di serie temporali cointegrate con Python
Applichiamo ora i test di radice unitaria su dati simulati che sappiamo cointegrati. Utilizziamo la definizione di cointegrazione delle serie temporali per generare artificialmente due serie non stazionarie che condividono una tendenza stocastica comune, ma la cui combinazione lineare è stazionaria.
Definiamo una passeggiata casuale \(z_t = z_{t-1} + w_t\), dove \(w_t\) è un rumore bianco.
Per approfondire questi concetti consigliamo di rileggere la lezione sul rumore bianco e le passeggiate casuali
A partire da \(z_t\) generiamo due nuove serie \(x_t\) e \(y_t\) che condividono la stessa tendenza stocastica di \(z_t\), anche se con ampiezze differenti:
\(\begin{eqnarray}x_t &=& p z_t + w_{x,t} \\
y_t &=& q z_t + w_{y,t}\end{eqnarray}\)
Consideriamo ora una combinazione lineare \(a x_t + b y_t\):
\(\begin{eqnarray}a x_t + b y_t &=& a (p z_t + w_{x,t}) + b (q z_t + w_{y,t}) \\
&=& (ap + bq) z_t + a w_{x,t} + b w_{y,t}\end{eqnarray}\)
Otteniamo una serie stazionaria — somma di rumori bianchi — se \(ap + bq = 0\). Valorizziamo ora i coefficienti: supponiamo \(p=0.3\) e \(q=0.6\). Calcoliamo \(ap + bq = 0\) scegliendo \(a=2\) e \(b=-1\), ottenendo così una combinazione stazionaria. Le serie \(x_t\) e \(y_t\) risultano quindi cointegrate quando \(a=2\) e \(b=-1\).
Procediamo ora a simulare queste serie con Python e a visualizzare la combinazione stazionaria, illustrando concretamente la cointegrazione delle serie temporali.
Random walk
In primo luogo, desideriamo creare e tracciare la serie di passeggiate casuali sottostante, \(z_t\):
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(123)
# 1. Generazione del random walk zₜ
z = np.zeros(1000)
for i in range(1, 1000):
z[i] = z[i-1] + np.random.normal()
# Plot di zₜ
plt.plot(z)
plt.show()
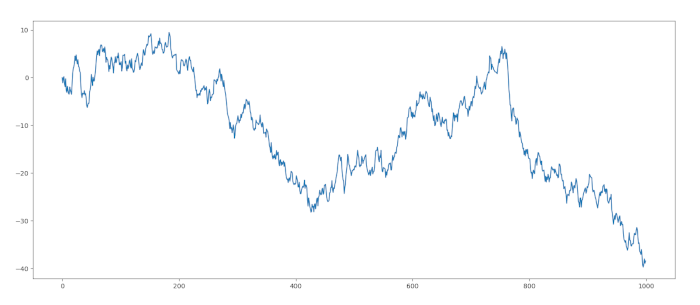
Se tracciamo il correlogramma della serie e quello delle sue differenze possiamo vedere poche evidenze di autocorrelazione:
from statsmodels.graphics.tsaplots import plot_acf
# 2. Correlogramma di zₜ e delle sue differenze
plot_acf(z, title="Serie z", alpha=0.05, lags=30)
plot_acf(np.diff(z), title="Variazioni assolute della Serie z", alpha=0.05, lags=30)
plt.show()
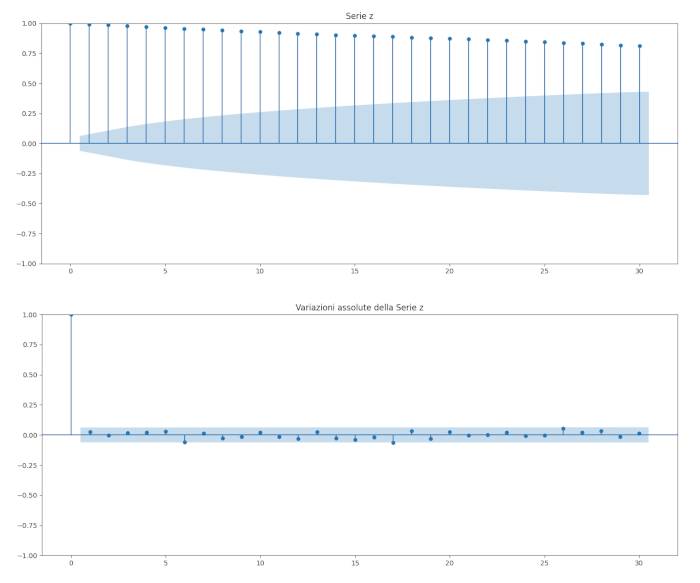
Combinazione lineare cointegrata
Da quanto sopra questa realizzazione di \(z_t\) sembra chiaramente una passeggiata casuale.
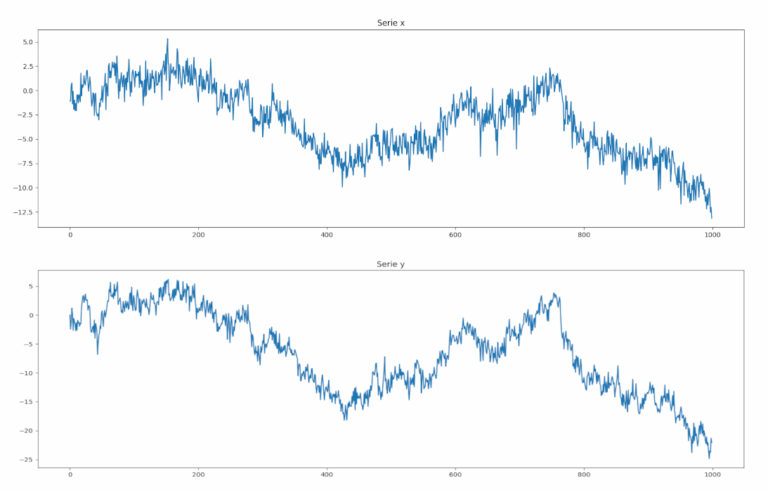
Il prossimo passo è creare \(x_t\) e \(y_t\) a partire da \(z_t\), usando \(p=0.3\) e \(q=0.6\), quindi tracciare i grafici di entrambe le serie:
x = 0.3 * z + np.random.normal(size=1000)
y = 0.6 * z + np.random.normal(size=1000)
plt.plot(x)
plt.title("Serie x")
plt.show()
plt.plot(y)
plt.title("Serie y")
plt.show()
Possiamo notare come grafici sono molto simili. Ovviamente lo sono per definizione: condividono la stessa struttura sottostrante di camminata casuale di \(z_t\).
Calcoliamo ora la combinazione lineare usando \(p=2\) e \(q=-1\) ed esaminiamo la struttura di autocorrelazione:
comb = 2 * x - y
plt.plot(comb)
plt.title("Serie 2x - y")
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(comb, lags=30)
plt.show()
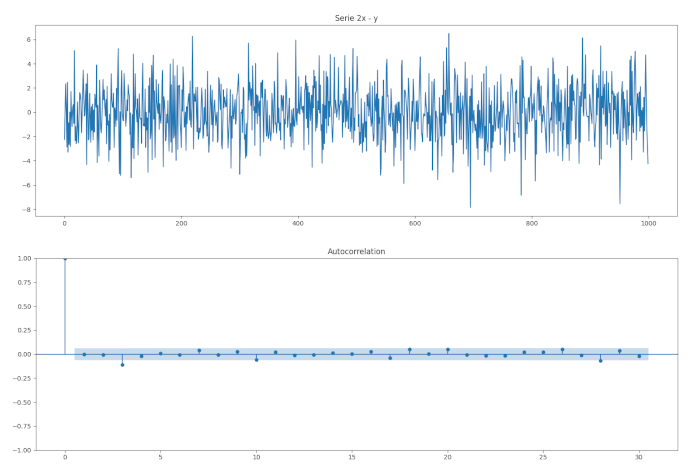
È evidente che la serie combinata comb assomiglia molto a una serie stazionaria. Questo era prevedibile dalla sua definizione.
Test della radice unitaria
Proviamo ad applicare i tre test della radice unitaria alla serie di combinazioni lineari. In primo luogo, il test Augmented Dickey-Fuller:
from arch.unitroot import ADF
adf = ADF(comb)
print(adf.summary())
Augmented Dickey-Fuller Results
=====================================
Test Statistic -20.307
P-value 0.000
Lags 2
-------------------------------------
Trend: Constant
Critical Values: -3.44 (1%), -2.86 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
Il P-value è piccolo e quindi abbiamo prove per rifiutare l’ipotesi nulla che la serie possieda una radice unitaria.
Proviamo il test di Phillips-Perron:
from arch.unitroot import PhillipsPerron
php = PhillipsPerron(comb)
print(php.summary())
Phillips-Perron Test (Z-tau)
=====================================
Test Statistic -31.725
P-value 0.000
Lags 22
-------------------------------------
Trend: Constant
Critical Values: -3.44 (1%), -2.86 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
Anche in questo caso abbiamo un piccolo P-value quindi abbiamo prove per rifiutare l’ipotesi nulla di una radice unitaria.
Infine, proviamo il test di Phillips-Ouliaris (questo test richiede in input la matrice dei costituenti della serie sottostante):
from arch.unitroot.cointegration import phillips_ouliaris
po = phillips_ouliaris(2*x_t, -1*y_t)
print(po.summary())
Phillips-Ouliaris Zt Cointegration Test
=====================================
Test Statistic -31.812
P-value 0.000
Kernel Bartlett
Bandwidth 6.259
-------------------------------------
Trend: Constant
Critical Values: -3.05 (10%), -3.35 (5%), -3.91 (1%)
Null Hypothesis: No Cointegration
Alternative Hypothesis: Cointegration
Distribution Order: 3
Ancora una volta vediamo un P-vaule piccolo e quindi possiamo rifiutare l’ipotesi nulla. E’ sufficiente per dimostrare che abbiamo una coppia di serie cointegrate.
Conclusione
In questo lezione abbiamo esaminato alcuni test di radice unitaria per valutare se una combinazione lineare di serie temporali sia stazionaria, cioè testare la cointegrazione delle serie temporali.
Questo approccio può essere implementato per creare strategie di trading di ritorno alla media per i dati giornalieri di azioni ed ETF.
Inoltre estendendo l’analisi alla cointegrazione di più asset, possiamo costruire strategie di trading che sfruttano portafogli cointegrati.
Riferimenti
- [1] Cowpertwait, P.S.P., Metcalfe, A.V. (2009) Introductory Time Series with R, Springer
- [2] Dickey, D.A., Fuller, W.A. (1979) “Distribution of the Estimators for Autoregressive Time Series with a Unit Root”, Journal of the American Statistical Association 74 (366): 427-431
- [3] Pfaff, B. (2010) Analysis of Integrated and Cointegrated Time Series with R, 2nd Ed., Springer
- [4] Phillips, P.C.B., Ouliaris, S. (1990) “Asymptotic Properties of Residual Based Tests for Cointegration”, Econometrica 58 (1): 165-193
- [5] Phillips, P.C.B., Perron, P. (1988) “Testing for a Unit Root in Time Series Regression”, Biometrika 75 (2): 335–346
- [6] Said, S.E., Dickey, D.A. (1984) “Testing for Unit Roots in Autoregressive-Moving Average Models of Unknown Order”, Biometrika 71 (3): 599-607
- [7] Zivot, E. (2006) Economics 584: Time Series Economics, Course Notes
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“