In questa lezione spieghiamo come generare più file CSV contenenti dati sintetici dei prezzi e dei volumi giornalieri di titoli azionari, utilizzando la soluzione analitica dell’equazione differenziale stocastica del moto browniano geometrico (GBM). Scriviamo il codice in Python e sviluppiamo una classe richiamabile tramite un’interfaccia a riga di comando (CLI), sfruttando la libreria click di Python. Utilizziamo anche NumPy e Pandas per simulare e analizzare i dati generati.
Moto Browniano Geometrico Simulato
Generare dati sintetici rappresenta una tecnica estremamente utile nella finanza quantitativa. Possiamo così valutare il comportamento dei modelli utilizzando dati dai pattern noti. Applichiamo questa tecnica in numerosi contesti, ad esempio per testare il corretto funzionamento dei simulatori di backtesting oppure per esplorare scenari ipotetici come crisi economiche, recessioni o eventi estremi.
Per generare dati sintetici, costruiamo un modello che descrive il comportamento dei dati. Scegliamo tra due approcci principali, oppure li combiniamo per creare modelli più sofisticati. Con l’approccio ‘model driven’, definiamo un modello “fisico” del comportamento dell’asset ed eseguiamo simulazioni basate su questo. Le equazioni differenziali stocastiche (SDE) rientrano in questa categoria. Con l’approccio ‘data driven’, stimiamo la distribuzione dei rendimenti da dati reali e la usiamo per creare nuove serie simulate dello stesso asset.
Con questa lezione, vogliamo non solo dimostrare come simulare i dati di prezzo e volume di un moto browniano geometrico , ma anche spiegare come sviluppare codice pronto per l’ambiente produttivo, come nel caso di un software per hedge fund quantitativi. Per motivi di brevità, non inseriamo una suite completa di test di integrazione, ma in contesti istituzionali questo rappresenta un requisito fondamentale.
Seguiamo una struttura chiara: iniziamo delineando l’architettura generale del programma e approfondiamo successivamente i metodi delle singole classi. Alla fine della lezione presentiamo l’intero codice funzionante.
Implementazione in Python
Iniziamo a codificare la simulazione il moto browniano geometrico con Python. Conserviamo l’intera struttura del codice in un singolo file chiamato gbm.py. Iniziamo con l’importazione delle librerie necessarie, definiamo poi la classe principale, integriamo l’interfaccia click di Python e infine aggiungiamo il punto di ingresso con il consueto if __name__ == "__main__".
# IMPORTAZIONE LIBRERIE
class GeometricBrownianMotionAssetSimulator:
def __init__(...):
...
def _SOME_CALCULATION_METHOD(...):
...
def __call__(...):
# CHIAMATA ALTRI METODI
# DEFINZIONE DEI PARAMETRI PER LA LINEA DI COMANDO CLICK
def cli(COMMAND_LINE_PARAMS):
gbmas = GeometricBrownianMotionAssetSimulator(...)
gbmas() # Qui si richiama la classe per eseguire la simulazione.
if __name__ == "__main__":
cli() # Uso di click come punto di ingresso
Dedichiamo ora attenzione al metodo __call__. In Python possiamo sovrascrivere alcuni metodi speciali, detti ‘dunder’, per ottenere comportamenti personalizzati. Uno di questi è proprio __call__. Se lo sovrascriviamo, possiamo richiamare direttamente l’oggetto istanziato della classe come se fosse una funzione. Questo approccio, molto potente, ci porta al concetto di oggetti funzione. In questo caso, preferiamo usare __call__ invece di creare un metodo come .run_class().
Dopo aver tracciato la struttura generale del codice, concentriamoci ora sui suoi singoli componenti.
Importazione delle librerie
Come primo passo, dichiariamo tutte le importazioni necessarie per lo script:
import os
import random
import string
import click
import numpy as np
import pandas as pd
Organizziamo le importazioni in ordine alfabetico all’interno di ciascun blocco: prima le librerie standard, poi quelle esterne, infine le eventuali librerie locali (che in questo esempio non compaiono). L’ordine alfabetico ci aiuta a verificare rapidamente la presenza di una specifica libreria.
Dalla libreria standard importiamo os per interagire con il filesystem e gestire l’output dei file CSV, random per garantire la riproducibilità delle simulazioni e string per generare simboli ticker casuali da usare nei nomi dei file CSV.
Tra le librerie esterne utilizziamo click, NumPy e Pandas.
Con Click creiamo un’interfaccia a riga di comando (CLI) che ci permette di parametrizzare ogni simulazione direttamente dal terminale, evitando valori hardcoded nei file di configurazione. Questo risulta molto utile, ad esempio, quando eseguiamo il codice su un cluster HPC con il sistema di schedulazione Slurm.
Utilizziamo NumPy per eseguire la simulazione matematica vera e propria tramite la soluzione analitica del GBM SDE, mentre Pandas ci consente di costruire un DataFrame con i prezzi di apertura, massimo, minimo, chiusura e volumi, da esportare in formato CSV su disco.
La classe per il moto browniano geometrico
La classe GBM per il moto browniano geometrico accetta numerosi parametri, così possiamo ottenere la massima flessibilità nelle simulazioni. Qui sotto riportiamo il codice che definisce la classe e il metodo di inizializzazione. Come tutti gli altri metodi, anche questo è ampiamente documentato:
class GeometricBrownianMotionAssetSimulator:
"""
Questa classe richiamabile genererà un DataFrame dei prezzi giornalieri di
apertura-massimo-minimo-chiusura-volumi (OHLCV) per simulare i percorsi di
prezzo delle azioni con il moto browniano geometrico per il prezzo e una
distribuzione di Pareto per il volume.
Produrrà i risultati in un CSV con un simbolo ticker generato casualmente.
Per ora lo strumento è hardcoded per generare dati giornalieri dei
giorni lavorativo tra due date, incluse.
Si noti che i dati sui prezzi e sul volume sono completamente non correlati,
il che non è probabile che si verifichi per i dati di asset reali.
Parameters
----------
start_date : `str`
La data di inizio nel formato AAAA-MM-GG.
end_date : `str`
La data di fine nel formato AAAA-MM-GG.
output_dir : `str`
Il percorso completo della directory di output per il file CSV.
symbol_length : `int`
La lunghezza da usare per il simbolo ticker.
init_price : `float`
Il prezzo iniziale dell'asset.
mu : `float`
La "deriva" media dell'asset.
sigma : `float`
La "volatilità" dell'asset.
pareto_shape : `float`
Il parametro utilizzato per governare la forma di distribuzione
di Pareto per la generazione dei dati di volume.
"""
def __init__(
self,
start_date,
end_date,
output_dir,
symbol_length,
init_price,
mu,
sigma,
pareto_shape
):
self.start_date = start_date
self.end_date = end_date
self.output_dir = output_dir
self.symbol_length = symbol_length
self.init_price = init_price
self.mu = mu
self.sigma = sigma
self.pareto_shape = pareto_shape
I commenti descrivono il significato di ogni parametro. In sostanza i parametri sono un set di date di inizio/fine, una directory di output in cui archiviare il file CSV, la lunghezza dei caratteri del simbolo ticker, nonché alcuni parametri statistici utilizzati per controllare la simulazione.
I parametri statistici includono la “deriva” e la “volatilità” della soluzione GBM, che possono essere modificate per generare titoli con una tendenza media più o meno al rialzo, nonché la loro volatilità. Si noti che questi valori sono costanti nel tempo. Cioè, il GBM non supporta la volatilità variabile nel tempo o “stocastica”.
Il parametro statistico finale è il pareto_shape. Questo governa la forma della distribuzione di Pareto utilizzata per simulare il volume degli scambi giornalieri. Tecnicamente, all’aumentare di questo valore la distribuzione di Pareto si avvicina a una funzione delta di Dirac a zero. Cioè, un valore maggiore genererà probabilmente valori più estremi del volume degli scambi.
Simulazione del ticker
Il primo metodo all’interno della classe crea semplicemente una stringa ticker randomizzata, come JFEFX, per un dato numero di caratteri. Utilizza le librerie standard stringe random per crearla in modo casuale dall’elenco di tutte le lettere maiuscole ASCII:
def _generate_random_symbol(self):
"""
Genera una stringa di simbolo ticker casuale composta da caratteri
ASCII maiuscoli da utilizzare nel nome file di output CSV.
Returns
-------
`str`
La stringa ticker casuale composta da lettere maiuscole.
"""
return ''.join(
random.choices(
string.ascii_uppercase,
k=self.symbol_length
)
)
DataFrame (inizialmente vuoto) di valori zero contenenti colonne per date, open, high, low, close e volume. Utilizza il metodo date_range di Pandas per produrre una serie di giorni lavorativi tra le date di inizio e di fine, inclusi:
def _create_empty_frame(self):
"""
Crea il DataFrame Pandas vuoto con una colonna date
utilizzando i giorni lavorativi tra due date. Ognuna
delle colonne prezzo/volume è impostata su zero.
Returns
-------
`pd.DataFrame`
DataFrame OHLCV vuoto per il popolamento successivo.
"""
date_range = pd.date_range(
self.start_date,
self.end_date,
freq='B'
)
zeros = pd.Series(np.zeros(len(date_range)))
return pd.DataFrame(
{
'date': date_range,
'open': zeros,
'high': zeros,
'low': zeros,
'close': zeros,
'volume': zeros
}
)[['date', 'open', 'high', 'low', 'close', 'volume']]
Simulazione dei prezzi
Il metodo successivo rappresenta il nucleo della classe e simula concretamente i possibili percorsi dei prezzi dell’asset. Questo metodo richiede alcune spiegazioni.
Per iniziare, definiamo il tempo di fine in anni, indicato con T. Poiché un anno conta circa 252 giorni lavorativi e i dati sono giornalieri, T corrisponde (approssimativamente) al numero di anni dei dati simulati.
Successivamente, calcoliamo dt, ovvero il timestep utilizzato per ogni successivo percorso dei prezzi dell’asset. Applichiamo un fattore quattro per simulare un percorso con quattro volte più dati, così da includere i valori di apertura, massimo, minimo e chiusura. In pratica, generiamo quattro prezzi per ciascun giorno e li analizziamo. Demandiamo il calcolo di minimi e massimi a un altro metodo.
Dopo aver definito la fase temporale, applichiamo in modo vettorializzato la formula corretta per il percorso dell’asset. Spieghiamo questa formula in dettaglio nella lezione dedicata.
Quando simuliamo tutti i singoli valori up/down del percorso dell’asset nella variabile asset_path, calcoliamo il loro prodotto cumulativo e lo moltiplichiamo per un valore iniziale di prezzo, così da ottenere un percorso realistico per un’azione o altro strumento finanziario.
def _create_geometric_brownian_motion(self, data):
"""
Calcola il percorso del prezzo di un asset utilizzando la
soluzione analitica dell'equazione differenziale stocastica
(SDE) del moto browniano geometrico.
Questo divide il solito timestep per quattro in modo che la
serie dei prezzi sia quattro volte più lunga, per tenere conto
della necessità di avere un prezzo di apertura, massimo, minimo
e chiusura per ogni giorno. Questi prezzi vengono successivamente
delimitati correttamente in un ulteriore metodo.
Parameters
----------
data : `pd.DataFrame`
Il DataFrame necessario per calcolare la lunghezza delle serie temporali.
Returns
-------
`np.ndarray`
Il percorso del prezzo dell'asset (quattro volte più lungo per includere OHLC).
"""
n = len(data)
T = n / 252.0 # Giorni lavorativi in un anno
dt = T / (4.0 * n) # 4.0 è necessario perchè sono richiesti quattro prezzi per ogni giorno
# implementazione vettorializzata per la generazione di percorsi di asset
# includendo quattro prezzo per ogni giorni, usati per creare OHLC
asset_path = np.exp(
(self.mu - self.sigma ** 2 / 2) * dt +
self.sigma * np.random.normal(0, np.sqrt(dt), size=(4 * n))
)
return self.init_price * asset_path.cumprod()
Calcolo dei massimi e minimi
Abbiamo detto che sono richiesti quattro prezzi per ogni giorno. Tuttavia, non vi era alcuna garanzia che i prezzi massimi e minimi simulati sarebbero stati effettivamente i prezzi massimi e minimi del giorno.
Quindi il seguente metodo regola i prezzi massimo/minimo prendendo i valori massimo/minimo su tutti i valori del giorno (inclusi i prezzi di apertura/chiusura) in modo tale che la “barra” OHLC sia calcolata correttamente. La notazione di slicing NumPy viene utilizzata per scorrere in incrementi di quattro, eseguendo efficacemente i calcoli su base giornaliera:
def _append_path_to_data(self, data, path):
"""
Tiene conto correttamente dei calcoli massimo/minimo necessari
per generare un prezzo massimo e minimo corretto per il
prezzo di un determinato giorno.
Il prezzo di apertura prende ogni quarto valore, mentre il
prezzo di chiusura prende ogni quarto valore sfalsato di 3
(ultimo valore in ogni blocco di quattro).
I prezzi massimo e minimo vengono calcolati prendendo il massimo
(risp. minimo) di tutti e quattro i prezzi in un giorno e
quindi aggiustando questi valori se necessario.
Tutto questo viene eseguito sul posto in modo che il frame
non venga restituito tramite il metodo.
Parameters
----------
data : `pd.DataFrame`
Il DataFrame prezzo/volume da modificare sul posto.
path : `np.ndarray`
L'array NumPy originale del percorso del prezzo dell'asset.
"""
data['open'] = path[0::4]
data['close'] = path[3::4]
data['high'] = np.maximum(
np.maximum(path[0::4], path[1::4]),
np.maximum(path[2::4], path[3::4])
)
data['low'] = np.minimum(
np.minimum(path[0::4], path[1::4]),
np.minimum(path[2::4], path[3::4])
)
Simulazione del Volume
In questa fase, il DataFrame include ora le colonne open, high, low e close. Tuttavia, dobbiamo ancora simulare il volume. Usiamo un campionamento vettorializzato da una distribuzione di Pareto per generare il volume scambiato giornalmente per un titolo. Il parametro shape della distribuzione determina l’entità dei valori generati, mentre il parametro size specifica quante estrazioni effettuare. Lo impostiamo in modo che corrisponda al numero di giorni presenti nel DataFrame.
Poiché la distribuzione di Pareto genera valori in virgola mobile, li ridimensioniamo e li convertiamo in numeri interi per evitare il problema delle “quote frazionarie” nella simulazione. Moltiplichiamo anche i valori generati dalla distribuzione di Pareto per un fattore scalare pari a \(10^6\), così da ottenere volumi giornalieri tipici delle azioni a grande capitalizzazione.
Osserviamo che i dati di volume non mostrano alcuna autocorrelazione, né risultano correlati al percorso dell’asset. Adottiamo queste assunzioni semplificative esclusivamente per i fini di questa lezione. Per realizzare un’implementazione più realistica, dobbiamo includere tali correlazioni nel modello.
def _append_volume_to_data(self, data):
"""
Utilizza una distribuzione di Pareto per simulare dati di volume
non negativi. Si noti che questo non è correlato al prezzo
dell'attività sottostante, come sarebbe probabilmente il caso dei
dati reali, ma è un'approssimazione ragionevolmente efficace.
Parameters
----------
data : `pd.DataFrame`
Il DataFrame a cui aggiungere i dati del volume, sul posto.
"""
data['volume'] = np.array(
list(
map(
int,
np.random.pareto(
self.pareto_shape,
size=len(data)
) * 1000000.0
)
)
)
Gestione dei dati
Il metodo successivo memorizza semplicemente il file CSV su disco assicurandosi di visualizzare solo due cifre decimali per le informazioni sui prezzi in virgola mobile:
def _output_frame_to_dir(self, symbol, data):
"""
Output the fully-populated DataFrame to disk into the
desired output directory, ensuring to trim all pricing
values to two decimal places.
Memorizza il DataFrame completamente popolato su disco
nella directory di output desiderata, assicurandosi di
ridurre tutti i valori dei prezzi a due cifre decimali.
Parameters
----------
symbol : `str`
Il simbolo ticker con cui denominare il file.
data : `pd.DataFrame`
DataFrame contenente i dati OHLCV generati.
"""
output_file = os.path.join(self.output_dir, '%s.csv' % symbol)
data.to_csv(output_file, index=False, float_format='%.2f')
Il metodo __call__ è la classe ‘entrypoint’. Come si può vedere, assembla semplicemente tutti i metodi descritti in precedenza e li esegue in sequenza. Si tratta di un approccio di “codice pulito” ampiamente utilizzato che assicura che sia semplice ispezionare la metodologia complessiva di elaborazione dei dati della classe:
def __call__(self):
"""
Il punto di ingresso per la generazione del frame OHLCV dell'asset. Si genera
un simbolo e un dataframe vuoto. Quindi popola questo dataframe con alcuni
dati GBM simulati. Il volume dell'asset viene quindi aggiunto a questi
dati e infine viene salvato su disco come CSV.
"""
symbol = self._generate_random_symbol()
data = self._create_empty_frame()
path = self._create_geometric_brownian_motion(data)
self._append_path_to_data(data, path)
self._append_volume_to_data(data)
self._output_frame_to_dir(symbol, data)
In questa fase, l’esecuzione del file non produce alcun risultato perché non abbiamo ancora istanziato o eseguito la classe. Ce ne occupiamo nella funzione cli(), che sfrutta la libreria Click.
Punto di ingresso con Click
Per completare e gestire il codice che simula un moto browniano geometrico usiamo la libreria Click. Con la libreria Click possiamo specificare un insieme di parametri da riga di comando, inclusi valori predefiniti opzionali e descrizioni utili. Lo schema standard prevede la definizione di una funzione chiamata cli, che accetta un insieme di nomi di parametri. Questi nomi corrispondono ai parametri generati tramite ciascun decoratore @click.option(...), indicando con precisione quale parametro mappiamo con un’opzione della riga di comando e in quale modalità.
Notiamo che l’insieme di parametri gestito da Click coincide quasi del tutto con quelli inseriti nella classe. Questo approccio ci permette di esporre efficacemente i parametri della classe tramite una CLI, integrandoli in un processo dati più ampio.
Separare la classe dal punto di ingresso Click ci offre il vantaggio di importare la classe in altri moduli Python senza doverla eseguire attraverso Click. Allo stesso tempo, possiamo anche eseguirla tramite CLI quando serve. Utilizzando questo schema su molte classi, otteniamo un notevole riutilizzo del codice tra strumenti diversi, risparmiando tempo e fatica negli sviluppi futuri.
Abbiamo già descritto tutti i parametri nel metodo di inizializzazione della classe, tranne num_assets, un intero che determina quanti file CSV distinti generare, cioè quanti titoli vogliamo simulare separatamente.
Dopo aver convertito correttamente i parametri nei rispettivi tipi, impostiamo il seed casuale di NumPy per garantire la completa riproducibilità dei dati a parità di seed fornito. In questo modo, i risultati coincidono perfettamente con quelli mostrati di seguito, se utilizziamo lo stesso seed e gli stessi parametri.
Implementazione
Infine, istanziamo la classe e la richiamiamo per ogni numero di asset desiderato, utilizzando il metodo __call__ descritto sopra. Lo facciamo chiamando la classe come una funzione, come mostrato nella riga seguente: gbmas().
@click.command()
@click.option('--num-assets', 'num_assets', default='1', help='Numero di asset separati per cui generare file')
@click.option('--random-seed', 'random_seed', default='42', help='Seed casuale da impostare sia per Python che per NumPy per la riproducibilità')
@click.option('--start-date', 'start_date', default=None, help='La data di inizio per la generazione dei dati sintetici nel formato AAAA-MM-GG')
@click.option('--end-date', 'end_date', default=None, help='La data di inizio per la generazione dei dati sintetici nel formato AAAA-MM-GG')
@click.option('--output-dir', 'output_dir', default=None, help='La posizione in cui inviare il file CSV di dati sintetici')
@click.option('--symbol-length', 'symbol_length', default='5', help='La lunghezza del simbolo dell''asset utilizzando caratteri ASCII maiuscoli')
@click.option('--init-price', 'init_price', default='100.0', help='Il prezzo iniziale da utilizzare')
@click.option('--mu', 'mu', default='0.1', help='Il parametro di deriva, \mu per GBM SDE')
@click.option('--sigma', 'sigma', default='0.3', help='Il parametro di volatilità, \sigma per SDE GBM')
@click.option('--pareto-shape', 'pareto_shape', default='1.5', help='La forma della distribuzione di Pareto che simula il volume degli scambi')
def cli(num_assets, random_seed, start_date, end_date, output_dir, symbol_length, init_price, mu, sigma, pareto_shape):
num_assets = int(num_assets)
random_seed = int(random_seed)
symbol_length = int(symbol_length)
init_price = float(init_price)
mu = float(mu)
sigma = float(sigma)
pareto_shape = float(pareto_shape)
# Seed per Python e NumPy
random.seed(random_seed)
np.random.seed(seed=random_seed)
gbmas = GeometricBrownianMotionAssetSimulator(
start_date,
end_date,
output_dir,
symbol_length,
init_price,
mu,
sigma,
pareto_shape
)
# Crea num_assets file tramite la chiamata
# ripetuta alla classe istanziata
for i in range(num_assets):
print('Generating asset path %d of %d...' % (i+1, num_assets))
gbmas()
Infine, per eseguire lo script è necessario creare un’istruzione if __name__ == "__main__": per dire effettivamente all’interprete Python di eseguire la funzione cli():
if __name__ == "__main__":
cli()
Concludiamo qui la descrizione del codice.
Esecuzione del codice
Ora possiamo eseguire il codice che simula un moto browniano geometrico direttamente dalla riga di comando. Tuttavia, lavoriamo sempre all’interno di un ambiente Python configurato correttamente, con tutte le dipendenze esterne installate (Click, NumPy e Pandas).
Il modo più semplice per configurare l’ambiente consiste nell’installare la distribuzione Anaconda Python, che possiamo scaricare gratuitamente sulla nostra macchina locale. Inoltre, installiamo eventualmente Click se non è già presente. A questo punto, apriamo un terminale e lanciamo il codice con il comando seguente:
python gbm.py --num-assets=5 --random-seed=41 --start-date='1993-01-01' --end-date='2017-12-31' --output-dir='.' --symbol-lenth=5 --init-price=100.0 --mu=0.1 --sigma=0.3 --pareto-shape=1.5
Con questo comando generiamo cinque file CSV separati nella stessa directory della posizione dello script che copre il periodo dall’inizio del 1993 fino alla fine del 2017, con vari valori utilizzati per le distribuzioni statistiche.
I grafici dei dati
Come controllo finale vale la pena caricare i dati tramite Pandas e visualizzarli tramite Matplotib. Un semplice script per raggiungere questo obiettivo è il seguente:
import matplotlib.pyplot as plt
import pandas as pd
if __name__ == "__main__":
# Cambiare BUAWV.csv nel simbolo del ticker desiderato
df = pd.read_csv('BUAWV.csv').set_index('date')
df[['open', 'high', 'low', 'close']].plot()
plt.show()
Questo produce un grafico simle al seguente:
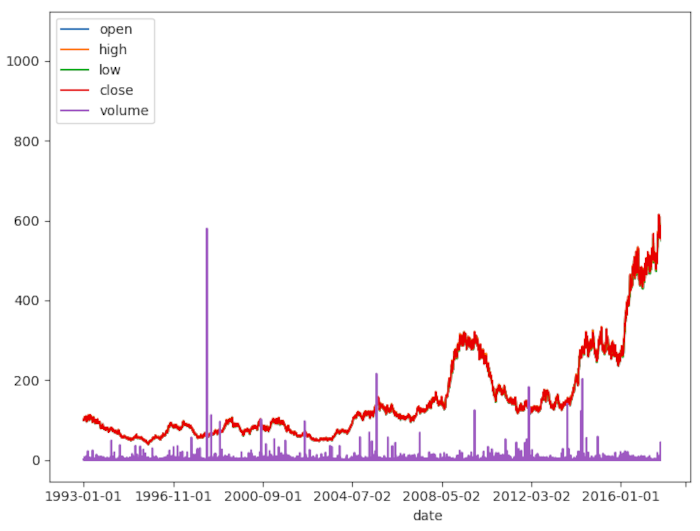
Osserviamo chiaramente il percorso dell’asset e il comportamento del volume, anche quando il volume presenta un multiplo molto ridotto.
Conclusioni
Sebbene la combinazione tra l’equazione differenziale stocastica del moto browniano geometrico e la distribuzione di Pareto generi un modello adeguato per simulare i percorsi degli asset, risulta ancora poco sofisticata rispetto ai dati reali dei titoli azionari. In particolare, non consideriamo fenomeni come l’inversione alla media, la volatilità stocastica, l’autocorrelazione tra prezzi e volumi, e altri comportamenti complessi delle serie temporali.
Nelle prossime lezioni modificheremo ed estenderemo la classe precedente per integrare modelli temporali più avanzati. Inoltre, mostreremo come eseguire lo strumento su un cluster Raspberry Pi, così da creare una libreria significativa di dati sintetici, utile per lo sviluppo e il test dei modelli di backtest.
Codice completo
import os
import random
import string
import click
import numpy as np
import pandas as pd
class GeometricBrownianMotionAssetSimulator:
"""
Questa classe richiamabile genererà un DataFrame dei prezzi giornalieri di
apertura-massimo-minimo-chiusura-volumi (OHLCV) per simulare i percorsi di
prezzo delle azioni con il moto browniano geometrico per il prezzo e una
distribuzione di Pareto per il volume.
Produrrà i risultati in un CSV con un simbolo ticker generato casualmente.
Per ora lo strumento è hardcoded per generare dati giornalieri dei
giorni lavorativo tra due date, incluse.
Si noti che i dati sui prezzi e sul volume sono completamente non correlati,
il che non è probabile che si verifichi per i dati di asset reali.
Parameters
----------
start_date : `str`
La data di inizio nel formato AAAA-MM-GG.
end_date : `str`
La data di fine nel formato AAAA-MM-GG.
output_dir : `str`
Il percorso completo della directory di output per il file CSV.
symbol_length : `int`
La lunghezza da usare per il simbolo ticker.
init_price : `float`
Il prezzo iniziale dell'asset.
mu : `float`
La "deriva" media dell'asset.
sigma : `float`
La "volatilità" dell'asset.
pareto_shape : `float`
Il parametro utilizzato per governare la forma di distribuzione
di Pareto per la generazione dei dati di volume.
"""
def __init__(
self,
start_date,
end_date,
output_dir,
symbol_length,
init_price,
mu,
sigma,
pareto_shape
):
self.start_date = start_date
self.end_date = end_date
self.output_dir = output_dir
self.symbol_length = symbol_length
self.init_price = init_price
self.mu = mu
self.sigma = sigma
self.pareto_shape = pareto_shape
def _generate_random_symbol(self):
"""
Genera una stringa di simbolo ticker casuale composta da caratteri
ASCII maiuscoli da utilizzare nel nome file di output CSV.
Returns
-------
`str`
La stringa ticker casuale composta da lettere maiuscole.
"""
return ''.join(
random.choices(
string.ascii_uppercase,
k=self.symbol_length
)
)
def _create_empty_frame(self):
"""
Crea il DataFrame Pandas vuoto con una colonna date
utilizzando i giorni lavorativi tra due date. Ognuna
delle colonne prezzo/volume è impostata su zero.
Returns
-------
`pd.DataFrame`
DataFrame OHLCV vuoto per il popolamento successivo.
"""
date_range = pd.date_range(
self.start_date,
self.end_date,
freq='B'
)
zeros = pd.Series(np.zeros(len(date_range)))
return pd.DataFrame(
{
'date': date_range,
'open': zeros,
'high': zeros,
'low': zeros,
'close': zeros,
'volume': zeros
}
)[['date', 'open', 'high', 'low', 'close', 'volume']]
def _create_geometric_brownian_motion(self, data):
"""
Calcola il percorso del prezzo di un asset utilizzando la
soluzione analitica dell'equazione differenziale stocastica
(SDE) del moto browniano geometrico.
Questo divide il solito timestep per quattro in modo che la
serie dei prezzi sia quattro volte più lunga, per tenere conto
della necessità di avere un prezzo di apertura, massimo, minimo
e chiusura per ogni giorno. Questi prezzi vengono successivamente
delimitati correttamente in un ulteriore metodo.
Parameters
----------
data : `pd.DataFrame`
Il DataFrame necessario per calcolare la lunghezza delle serie temporali.
Returns
-------
`np.ndarray`
Il percorso del prezzo dell'asset (quattro volte più lungo per includere OHLC).
"""
n = len(data)
T = n / 252.0 # Giorni lavorativi in un anno
dt = T / (4.0 * n) # 4.0 è necessario perchè sono richiesti quattro prezzi per ogni giorno
# implementazione vettorializzata per la generazione di percorsi di asset
# includendo quattro prezzo per ogni giorni, usati per creare OHLC
asset_path = np.exp(
(self.mu - self.sigma ** 2 / 2) * dt +
self.sigma * np.random.normal(0, np.sqrt(dt), size=(4 * n))
)
return self.init_price * asset_path.cumprod()
def _append_path_to_data(self, data, path):
"""
Tiene conto correttamente dei calcoli massimo/minimo necessari
per generare un prezzo massimo e minimo corretto per il
prezzo di un determinato giorno.
Il prezzo di apertura prende ogni quarto valore, mentre il
prezzo di chiusura prende ogni quarto valore sfalsato di 3
(ultimo valore in ogni blocco di quattro).
I prezzi massimo e minimo vengono calcolati prendendo il massimo
(risp. minimo) di tutti e quattro i prezzi in un giorno e
quindi aggiustando questi valori se necessario.
Tutto questo viene eseguito sul posto in modo che il frame
non venga restituito tramite il metodo.
Parameters
----------
data : `pd.DataFrame`
Il DataFrame prezzo/volume da modificare sul posto.
path : `np.ndarray`
L'array NumPy originale del percorso del prezzo dell'asset.
"""
data['open'] = path[0::4]
data['close'] = path[3::4]
data['high'] = np.maximum(
np.maximum(path[0::4], path[1::4]),
np.maximum(path[2::4], path[3::4])
)
data['low'] = np.minimum(
np.minimum(path[0::4], path[1::4]),
np.minimum(path[2::4], path[3::4])
)
def _append_volume_to_data(self, data):
"""
Utilizza una distribuzione di Pareto per simulare dati di volume
non negativi. Si noti che questo non è correlato al prezzo
dell'attività sottostante, come sarebbe probabilmente il caso dei
dati reali, ma è un'approssimazione ragionevolmente efficace.
Parameters
----------
data : `pd.DataFrame`
Il DataFrame a cui aggiungere i dati del volume, sul posto.
"""
data['volume'] = np.array(
list(
map(
int,
np.random.pareto(
self.pareto_shape,
size=len(data)
) * 1000000.0
)
)
)
def _output_frame_to_dir(self, symbol, data):
"""
Output the fully-populated DataFrame to disk into the
desired output directory, ensuring to trim all pricing
values to two decimal places.
Memorizza il DataFrame completamente popolato su disco
nella directory di output desiderata, assicurandosi di
ridurre tutti i valori dei prezzi a due cifre decimali.
Parameters
----------
symbol : `str`
Il simbolo ticker con cui denominare il file.
data : `pd.DataFrame`
DataFrame contenente i dati OHLCV generati.
"""
output_file = os.path.join(self.output_dir, '%s.csv' % symbol)
data.to_csv(output_file, index=False, float_format='%.2f')
def __call__(self):
"""
Il punto di ingresso per la generazione del frame OHLCV dell'asset. Si genera
un simbolo e un dataframe vuoto. Quindi popola questo dataframe con alcuni
dati GBM simulati. Il volume dell'asset viene quindi aggiunto a questi
dati e infine viene salvato su disco come CSV.
"""
symbol = self._generate_random_symbol()
data = self._create_empty_frame()
path = self._create_geometric_brownian_motion(data)
self._append_path_to_data(data, path)
self._append_volume_to_data(data)
self._output_frame_to_dir(symbol, data)
@click.command()
@click.option('--num-assets', 'num_assets', default='1', help='Numero di asset separati per cui generare file')
@click.option('--random-seed', 'random_seed', default='42', help='Seed casuale da impostare sia per Python che per NumPy per la riproducibilità')
@click.option('--start-date', 'start_date', default=None, help='La data di inizio per la generazione dei dati sintetici nel formato AAAA-MM-GG')
@click.option('--end-date', 'end_date', default=None, help='La data di inizio per la generazione dei dati sintetici nel formato AAAA-MM-GG')
@click.option('--output-dir', 'output_dir', default=None, help='La posizione in cui inviare il file CSV di dati sintetici')
@click.option('--symbol-length', 'symbol_length', default='5', help='La lunghezza del simbolo dell''asset utilizzando caratteri ASCII maiuscoli')
@click.option('--init-price', 'init_price', default='100.0', help='Il prezzo iniziale da utilizzare')
@click.option('--mu', 'mu', default='0.1', help='Il parametro di deriva, \mu per GBM SDE')
@click.option('--sigma', 'sigma', default='0.3', help='Il parametro di volatilità, \sigma per SDE GBM')
@click.option('--pareto-shape', 'pareto_shape', default='1.5', help='La forma della distribuzione di Pareto che simula il volume degli scambi')
def cli(num_assets, random_seed, start_date, end_date, output_dir, symbol_length, init_price, mu, sigma, pareto_shape):
num_assets = int(num_assets)
random_seed = int(random_seed)
symbol_length = int(symbol_length)
init_price = float(init_price)
mu = float(mu)
sigma = float(sigma)
pareto_shape = float(pareto_shape)
# Seed per Python e NumPy
random.seed(random_seed)
np.random.seed(seed=random_seed)
gbmas = GeometricBrownianMotionAssetSimulator(
start_date,
end_date,
output_dir,
symbol_length,
init_price,
mu,
sigma,
pareto_shape
)
# Crea num_assets file tramite la chiamata
# ripetuta alla classe istanziata
for i in range(num_assets):
print('Generating asset path %d of %d...' % (i+1, num_assets))
gbmas()
if __name__ == "__main__":
cli()
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

