In questa lezione presentiamo un metodo di machine learning statistico noto come Decision Tree. Utilizziamo gli alberi decisionali (DT) come tecnica di apprendimento supervisionato per stimare o prevedere i valori delle risposte tramite l’apprendimento di regole decisionali basate sulle feature. Applichiamo questa tecnica sia in contesti di regressione sia di classificazione, motivo per cui li definiamo anche come Classification And Regression Trees (CART).
Consideriamo i modelli DT/CART come esempi della più ampia categoria di modelli noti come adaptive basis function models. Invece di prespecificare le feature, le apprendiamo direttamente dai dati. A differenza della regressione lineare, questi modelli non risultano lineari nei parametri, per cui calcoliamo una stima di massima verosimiglianza (MLE) localmente ottimale per i parametri [1].
Applichiamo i modelli DT/CART suddividendo lo spazio delle caratteristiche in semplici regioni rettangolari, allineate agli assi. Per effettuare una previsione su una nuova osservazione, utilizziamo la media o la modalità delle risposte delle osservazioni di addestramento presenti nella partizione corrispondente.
Adottiamo i DT/CART per il loro principale vantaggio: generano in modo diretto un set interpretabile di regole decisionali if-then-else, simili ai diagrammi di flusso. Tuttavia, riconosciamo che presentano uno svantaggio: non raggiungono in genere la precisione delle altre tecniche supervisionate come le support vector machines o le deep neural networks in termini di accuratezza predittiva.
Rendiamo i DT/CART altamente competitivi integrandoli in metodi ensemble come il bagging, le random forest e il boosting.
Nella finanza quantitativa, utilizziamo insiemi di modelli DT/CART per prevedere sia i prezzi o le direzioni future degli asset, sia la liquidità di determinati strumenti. Nelle prossime lezioni, descriveremo strategie di trading basate su questi metodi.
Panoramica matematica
Considerando una specifica funzione di base adattiva probabilistica, definiamo il modello \(f({\bf x})\) come [1]:
\(\begin{eqnarray}f({\bf x}) = \mathbb{E}(y \mid {\bf x}) = \sum^{M}_{m=1} w_m \phi({\bf x}; {\bf v}_m)\end{eqnarray}\)
Indichiamo con \(w_m\) la risposta media in una regione specifica, \(R_m\), e con \({\bf v}_m\) il modo in cui dividiamo ciascuna variabile in base a un valore di soglia. Con queste divisioni strutturiamo lo spazio delle feature \(R^p\) in \(M\) diverse regioni iperrettangolari.
Decision tree per la regressione
Analizziamo un esempio astratto di regressione con due variabili caratteristiche (\(X_1\), \(X_2\)) e una risposta numerica \(y\). Così visualizziamo facilmente come l’albero effettua il partizionamento.
Osserviamo nella figura seguente un albero pre-addestrato costruito per questo esempio specifico:

In che modo questo corrisponde a una partizione dello spazio delle feature? La figura seguente mostra un sottoinsieme di \(\mathbb{R}^2\) che contiene i dati del nostro esempio. Notiamo come il dominio viene partizionato utilizzando le divisioni parallele all’asse. Ovvero, ogni divisione del dominio è allineata con uno degli assi delle feature:
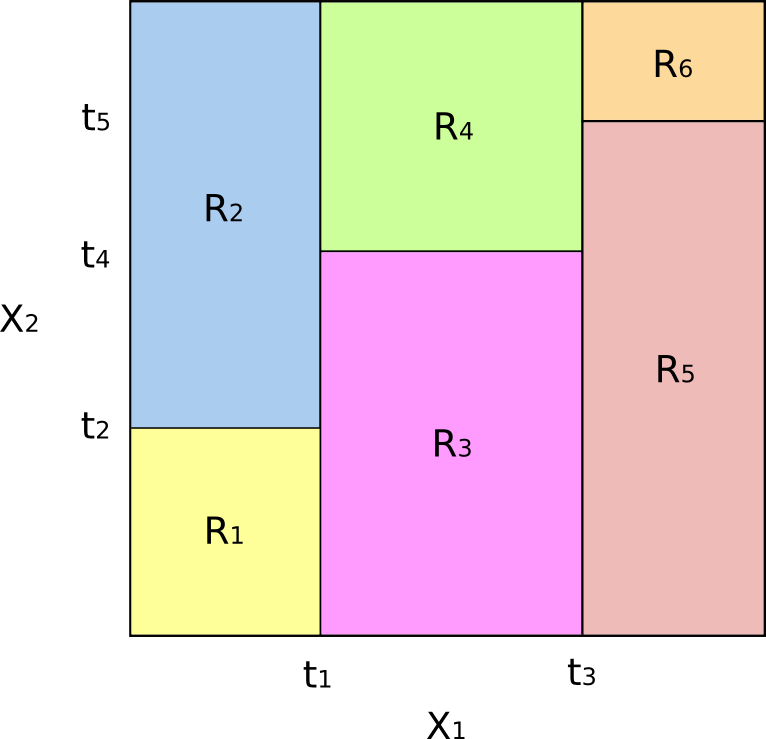
Estendiamo direttamente il concetto di divisione in assi paralleli a dimensioni maggiori di due. In uno spazio delle feature di dimensione p, cioè un sottoinsieme di \(\mathbb{R}^p\), suddividiamo lo spazio in M regioni, \(R_m\), ognuna delle quali costituisce un iperblocco a p dimensioni.
Descriviamo ora come “cresciamo” o “addestriamo” l’albero. Il paragrafo seguente presenta l’algoritmo che seguiamo per completare questa operazione.
Creiamo un albero di regressione e formuliamo previsioni
L’euristica che adottiamo per costruire un albero di decisione (DT) segue questi passi:
- Considerando p feature, partizioniamo lo spazio delle feature a p dimensioni (un sottoinsieme di \(\mathbb{R}^p\)) in M regioni reciprocamente distinte, che coprono interamente lo spazio e non si sovrappongono. Indichiamo queste regioni con \(R_1,…,R_M\).
- Per ogni nuova osservazione che cade in una specifica partizione \(R_m\), stimiamo la risposta calcolando la media delle osservazioni di addestramento appartenenti alla stessa partizione, indicata con \(w_m\).
Tuttavia, questa descrizione non ci dice come determinare le partizioni in modo algoritmico. Per farlo, adottiamo una tecnica nota come Recursive Binary Splitting (RBS)[2].
Applichiamo la divisione binaria ricorsiva (Recursive Binary Splitting)
Miriamo a ridurre un criterio di errore, in particolare la somma residua dei quadrati (RSS), utilizzata anche nella regressione lineare. Quando suddividiamo lo spazio delle feature in M partizioni, calcoliamo l’RSS con la formula:
\(\begin{eqnarray}\text{RSS} = \sum^{M}_{m=1} \sum_{i \in R_m} ( y_i – \hat{y}_{R_m} )^2\end{eqnarray}\)
Sommiamo dapprima su tutte le partizioni dello spazio delle feature (prima sommatoria), quindi sommiamo su tutte le osservazioni di test (indice i) all’interno di ogni partizione. Calcoliamo il quadrato della differenza tra la risposta \(y_i\) di una data osservazione e la media delle risposte \(\hat{y}_{R_m}\) nelle osservazioni di addestramento della stessa partizione.
Purtroppo, considerare tutte le possibili partizioni dello spazio delle feature in M rettangoli risulta troppo oneroso computazionalmente, dato che si tratta di un problema NP-completo. Per questo motivo adottiamo un metodo di ricerca meno costoso ma più sofisticato, come il Recursive Binary Splitting (RBS).
Con il RBS iniziamo dalla radice dell’albero, dividendola in due rami, generando così due partizioni. Ripetiamo questa suddivisione nella parte superiore dell’albero e selezioniamo quella che minimizza l’RSS corrente.
Proseguiamo creando un nuovo ramo nella partizione scelta, ripetiamo la procedura, valutiamo l’RSS a ogni split e scegliamo la suddivisione migliore.
Questa strategia rende l’algoritmo avido: valutiamo le scelte a ogni iterazione anziché esplorare tutte le diramazioni prima di decidere. Proprio questa caratteristica “avida” garantisce la fattibilità computazionale dell’approccio e ne consente l’utilizzo pratico [1], [2].
Non abbiamo ancora stabilito quando fermare la procedura. Possiamo adottare diversi criteri: impostare una profondità massima dell’albero, garantire un numero minimo di esempi di addestramento in ogni regione o assicurare una certa omogeneità tra le osservazioni, mantenendo così l’albero bilanciato.
Come per tutti i metodi di machine learning supervisionato, dobbiamo restare vigili rispetto all’overfitting. Questo ci porta a introdurre il concetto di “potatura” (pruning) dell’albero.
Pottiamo l’albero
Per limitare il rischio di overfitting e gestire al meglio il compromesso bias-varianza, regoliamo il processo di divisione dell’albero per ottenere una buona generalizzazione sugli insiemi di test.
Dato che applicare la convalida incrociata a ogni possibile sottoalbero durante l’addestramento è troppo costoso, scegliamo un approccio alternativo che assicura comunque un buon tasso di errore di test.
Il metodo classico consiste nel far crescere completamente l’albero fino a una profondità prefissata, per poi eseguire una procedura nota come “potatura”. Una delle strategie più usate è il cost-complexity pruning, descritto in dettaglio in [2] e [3]. Questo approccio introduce un parametro di ottimizzazione, \(\alpha\), che bilancia profondità dell’albero e capacità di adattamento ai dati di addestramento. Il metodo è simile alla tecnica LASSO di Tibshirani.
Non entriamo nei dettagli tecnici della potatura perché utilizziamo la libreria Scikit-Learn per implementare questa procedura.
Decision Tree per la classificazione
Finora abbiamo esplorato i Decision Tree applicati alla regressione, ma gli alberi decisionali si rivelano altrettanto efficaci nella classificazione: da qui la “C” nei modelli CART! L’unica differenza, come in tutti i contesti di classificazione, riguarda la previsione di un valore categorico per la variabile di risposta, invece di un valore continuo. Per prevedere una classe di categoria, usiamo la moda della regione di addestramento in cui si trova l’osservazione, al posto della media. In altre parole, assegniamo all’osservazione la classe più frequente. Inoltre, adottiamo criteri alternativi per dividere gli alberi, poiché non possiamo applicare il punteggio RSS nel contesto categoriale. Consideriamo tre criteri alternativi: la “hit rate”, l’indice di Gini e la Cross-Entropy [1], [2], [3].Classificazione Error Rate/Hit Rate
Invece di calcolare quanto una risposta numerica si discosta dal valore medio, come nella regressione, definiamo la “frequenza di successo” (hit rate) come la frazione di osservazioni di addestramento in una regione che non rientrano nelle classi più comuni. Cioè, calcoliamo l’errore nel modo seguente [1], [2]:\(\begin{eqnarray}E = 1 – \text{argmax}_{c} (\hat{\pi}_{mc})\end{eqnarray}\)
Dove \(\hat{\pi}_{mc}\) rappresenta la frazione di dati di addestramento nella regione \(R_m\) che appartengono alla classe c.Indice di Gini
Utilizziamo l’indice di Gini come metrica alternativa per valutare l’errore. Questo indice misura quanto una regione è “pura”, cioè quanto i dati di addestramento in una regione appartengono a una sola classe. Se una regione \(R_m\) contiene dati prevalentemente da una sola classe c, allora otteniamo un valore basso dell’indice di Gini:\(\begin{eqnarray}G = \sum_{c=1}^C \hat{\pi}_{mc} (1 – \hat{\pi}_{mc})\end{eqnarray}\)
Entropia incrociata (o devianza)
Una terza alternativa, simile all’indice di Gini, è la Cross-Entropy o Devianza:\(\begin{eqnarray}D = – \sum_{c=1}^C \hat{\pi}_{mc} \text{log} \hat{\pi}_{mc}\end{eqnarray}\)
A questo punto sorge la domanda su quale metrica di errore utilizzare durante l’addestramento di un albero di classificazione. Per massimizzare l’accuratezza della previsione, preferiamo l’Indice di Gini e la Devianza rispetto all’Hit Rate. Non entriamo nei dettagli di questa scelta, ma nel paragrafo “Riferimenti” riportiamo testi con ottime discussioni sull’argomento.Vantaggi e svantaggi dei Decision Tree
Come in ogni metodo di machine learning, anche i modelli DT/CART presentano vantaggi e svantaggi rispetto ad altri approcci:Vantaggi
- Comprendiamo facilmente i modelli DT/CART grazie alla loro struttura basata su regole “if-else”.
- Lavoriamo con feature categoriali e continue all’interno dello stesso dataset senza problemi.
- Affidiamo al metodo stesso la selezione automatica delle variabili, evitando la selezione manuale di sottoinsiemi.
- Applichiamo questi modelli con efficienza anche a grandi dataset.
Svantaggi
- Otteniamo prestazioni di previsione inferiori rispetto ad altri modelli di machine learning.
- Riscontriamo instabilità: piccoli cambiamenti nello spazio delle feature modificano sensibilmente il modello. In termini di bias-varianza, trattiamo modelli ad alta varianza.
Nota bibliografica
Una guida introduttiva ai metodi basati sui Decision Tree è disponibile in James et al. (2013) [2], che copre le basi sia dei DT che dei relativi metodi ensemble. Per un approccio più rigoroso, a livello universitario avanzato in matematica/statistica, consigliamo Hastie et al. (2009) [3]. Murphy (2012) [1] descrive i modelli di funzione di base adattiva, di cui i modelli DT/CART costituiscono un sottoinsieme, trattando sia l’approccio frequentista che quello bayesiano. Infine, per chi lavora con dati del “mondo reale” come i quants, Kuhn et al. (2013) [4] rappresenta un testo accessibile e molto utile.Riferimenti
- [1] Murphy, K.P. (2012) Machine Learning A Probabilistic Perspective, MIT Press
- [2] James, G., Witten, D., Hastie, T., Tibshirani, R. (2013) An Introduction to Statistical Learning, Springer
- [3] Hastie, T., Tibshirani, R., Friedman, J. (2009) The Elements of Statistical Learning, Springer
- [4] Kuhn, M., Johnson, K. (2013) Applied Predictive Modeling, Springer
Il codice completo per l’hedge ratio dinamico tra ETF, presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

