I Decision Tree (DT) rappresentano metodi di apprendimento supervisionato. Il loro punto di forza risiede nella capacità di offrire ottime prestazioni predittive quando li combiniamo in un insieme statistico (statistical ensemble). In questa lezione spieghiamo come miglioriamo notevolmente le previsioni combinando più DT in un ensemble di Decision Tree.
Ensemble di Decision Tree
Applichiamo queste tecniche non solo ai DT, ma anche a molti altri modelli di machine learning, sia per la regressione che per la classificazione. Tuttavia, i DT offrono una configurazione “naturale” per spiegare i metodi per creare un ensemble di decision tree d’insieme e li associamo comunemente tra loro.
Dopo aver esposto la teoria dei metodi d’insieme, mostriamo come li implementiamo in Python usando la libreria Scikit-Learn applicata ai dati finanziari. Se non abbiamo ancora familiarità con gli alberi decisionali, suggeriamo di leggere la lezione precedente prima di addentrarci nei metodi ensemble.
Prima di esplorare le tecniche ensemble come bootstrap aggregation (bagging), random forest e boosting, introduciamo una tecnica di statistica frequentista nota come bootstrap, che rende possibile l’applicazione di queste tecniche.
Il Bootstrap
Il Bootstrapping [1] consiste in una tecnica di ricampionamento statistico che prevede il campionamento casuale di un set di dati con sostituzione. Usiamo spesso questo metodo per quantificare l’incertezza associata a un modello di machine learning.
Nel contesto della finanza quantitativa, sfruttiamo il bootstrapping per generare nuovi campioni da una popolazione, senza raccogliere ulteriori “dati di addestramento”. Infatti, con i dati finanziari, non possiamo ottenere nuovi campioni dai prezzi degli asset, poiché abbiamo a disposizione una sola “storia” da cui attingere.
Puntiamo a produrre molti training set distinti tramite il campionamento ripetuto con sostituzione del training set originale. Li utilizziamo per permettere ai metodi “meta-learner” o “ensemble” di ridurre la varianza delle previsioni e migliorare le performance predittive.
Due tecniche ensemble di decision tree che sfruttiamo ampiamente il bootstrapping sono il bagging e le foreste casuali.
Aggregazione bootstrap (Bagging)
Come spiegato nella lezione sulla teoria dei Decision Tree, uno svantaggio chiave dei DT è la loro elevata varianza (high-variance estimator). Basta aggiungere poche osservazioni al set di addestramento per alterare drasticamente le previsioni, anche se i dati non cambiano in modo significativo.
Al contrario, un low-variance estimator come la regressione lineare risente poco dell’aggiunta di nuovi punti, purché siano vicini agli altri dati disponibili.
Affrontiamo questo problema adottando l’aggregazione bootstrap, o bagging. L’idea consiste nel combinare più modelli (ad esempio DT), ciascuno addestrato su diversi campioni bootstrap, e calcolare la media delle loro previsioni per ridurre la varianza complessiva.
Come indicano James et al. (2013) [2], se abbiamo N osservazioni indipendenti e distribuite in modo identico (iid) \(Z_1, \ldots, Z_N\), ognuna con varianza \(\sigma^2\), allora la varianza della loro media \(\bar{Z}\) è \(\sigma^2 / N\). In pratica, se calcoliamo la media, riduciamo la varianza in proporzione al numero di osservazioni. Questo conferma l’efficacia del bagging.
Nella finanza quantitativa, però, disponiamo spesso di un solo set di dati di “training”. In tali casi, generiamo diversi set di training tramite il bootstrap, partendo da un dataset più ampio.
Sulla base di James et al. (2013) [2] e dell’articolo su Wikipedia sulle Random Forest [3], se generiamo \(B\) campioni bootstrap del training set, e otteniamo stime dai modelli \(\hat{f}^b ({\bf x})\), allora possiamo calcolare un modello medio a bassa varianza, \(\hat{f}_{\text{avg}}\):
\(\begin{eqnarray}\hat{f}_{\text{avg}} ({\bf x}) = \frac{1}{B} \sum^{B}_{b=1} \hat{f}^b ({\bf x})\end{eqnarray}\)
Chiamiamo questa procedura bagging [4]. La applichiamo ai DT poiché si comportano da “high-variance estimators”, quindi il bagging li rende molto più stabili.
Applicazioni del bagging
Applichiamo il bagging ai DT in modo semplice. Costruiamo centinaia o migliaia di alberi molto profondi (non potati) usando \(B\) campioni bootstrap del set di addestramento. Combiniamo i risultati come descritto e riduciamo notevolmente la varianza.
Uno dei principali vantaggi del bagging è che, aumentando \(B\), non rischiamo di sovradimensionare il modello. Questo vale anche per le Random Forest, ma non per gli alberi potenziati.
Questo miglioramento della precisione riduce però l’interpretabilità del modello. Tuttavia, nella ricerca quantitativa privilegiamo la precisione grezza rispetto all’interpretabilità. Perciò, questo non rappresenta un problema rilevante nelle strategie di trading algoritmico.
Ricordiamo che esistono metodi statistici specifici per identificare le variabili importanti nel bagging, ma non rientrano nello scopo di questa lezione.
Random Forest
Le foreste casuali [5] seguono un approccio molto simile al bagging, ma introducono una tecnica chiamata feature bagging, che riduce in modo significativo la correlazione tra gli alberi decisionali (DT), migliorando così l’accuratezza predittiva complessiva.
Applichiamo il feature bagging selezionando casualmente un sottoinsieme delle feature di dimensione p a ogni nodo di suddivisione durante la crescita dei singoli alberi. Anche se potrebbe sembrare controintuitivo, preferiamo non usare tutte le feature per ridurre il rischio di ottenere alberi troppo simili tra loro.
In pratica, se una feature risulta molto predittiva, finisce spesso nei nodi di suddivisione di molti alberi. In questo modo il bagging tradizionale genera alberi fortemente correlati tra loro. Le foreste casuali evitano questo effetto ignorando intenzionalmente queste feature dominanti in molti alberi.
Quando utilizziamo tutte le p feature in ogni nodo, otteniamo il classico ensemble. Una buona regola pratica per le foreste casuali consiste nell’utilizzare \(\sqrt{p}\) feature, opportunamente arrotondate, per ogni divisione.
Ora presentiamo il codice Python che ci permette di confrontare le prestazioni tra foreste casuali e bagging, osservando l’effetto dell’aumento del numero di alberi decisionali usati come stimatori base.
Boosting
Un altro potente metodo ensemble nel machine learning è il boosting degli alberi. A differenza del bagging, il boosting non prevede il campionamento bootstrap. Generiamo i modelli in modo sequenziale e iterativo, tenendo conto del modello \(i\) prima di passare all’iterazione successiva \(i+1\).
Kearns e Valiant (1989) [6] hanno introdotto il boosting per unire modelli deboli di machine learning in un modello forte. In questo contesto, un modello debole supera di poco la probabilità casuale, mentre un modello forte si avvicina molto alla risposta reale.
Questa idea ci ha portato a sviluppare l’approccio iterativo: alleniamo ripetutamente modelli deboli su un dataset aggiornato, poi combiniamo questi modelli per ottenere un predittore finale e robusto. A differenza del bagging, non calcoliamo una semplice media su più campioni bootstrap.
James et al. (2013) [2] e Hastie et al. (2009) [7] descrivono così l’algoritmo di base per il boosting:
- Impostiamo l’estimatore iniziale a zero, cioè \(\hat{f}({\bf x}) = 0\), e definiamo i residui come \(r_i = y_i\) per ogni elemento del training set.
- Definiamo il numero di alberi potenziati \(B\) ed eseguiamo il seguente ciclo per \(b=1,\ldots,B\):
- Alleniamo un albero \(\hat{f}^b\) con k suddivisioni sui dati \((x_i, r_i)\), per ogni i.
- Aggiorniamo l’estimatore finale sommando l’albero scalato: \(\hat{f} ({\bf x}) \leftarrow \hat{f} ({\bf x}) + \lambda \hat{f}^b ({\bf x})\)
- Aggiorniamo i residui in base al nuovo modello: \(r_i \leftarrow r_i – \lambda \hat{f}^b (x_i)\)
- Definiamo il modello finale come somma dei modelli deboli: \(\hat{f}({\bf x}) = \sum_{b=1}^B \lambda \hat{f}^b ({\bf x})\)
Notiamo che ogni albero successivo si adatta ai residui prodotti dal modello precedente, migliorando così le performance nelle aree in cui il modello precedente risultava debole.
Vantaggi e Svantaggi
Sottolineiamo che l’ordine di addestramento degli alberi influisce fortemente sul boosting. Questo approccio “impara lentamente”, ma di solito offre prestazioni elevate. Non a caso, molti dei modelli vincenti nelle competizioni Kaggle usano il boosting.
Per il boosting, gestiamo tre iperparametri principali: la profondità degli alberi \(k\), il numero di alberi potenziati \(B\) e il tasso di apprendimento \(\lambda\). Possiamo scegliere alcuni di questi valori tramite convalida incrociata.
Un limite del boosting è il suo carattere iterativo: non possiamo parallelizzare facilmente il processo, a differenza del bagging, che invece lo consente.
Tra i principali algoritmi di boosting ricordiamo AdaBoost, xgboost e LogitBoost. Prima dell’avvento delle reti neurali profonde, gli alberi potenziati erano (e restano!) una delle tecniche di classificazione migliori “out of the box”.
Nel prossimo paragrafo confrontiamo boosting e bagging, focalizzandoci sul caso degli alberi decisionali.
Ensemble di decision tree con Python Scikit-Learn
Applichiamo ora i tre metodi di ensemble di decision tree (bagging, random forest e boosting) per prevedere i rendimenti giornalieri delle azioni Amazon, utilizzando i dati dei tre giorni precedenti.
Questo compito si rivela complesso, poiché i titoli ad alta liquidità, come Amazon, mostrano un basso rapporto segnale-rumore. Inoltre, i dati presentano correlazione seriale, il che compromette l’indipendenza dei campioni e può danneggiare la validità statistica.
Nelle prossime lezioni applichiamo una procedura più robusta, sfruttando la convalida incrociata per serie temporali disponibile in Scikit-Learn. Per ora, preferiamo una suddivisione standard training-test, dato che in questa lezione ci concentriamo sul confronto tra modelli, non sull’errore assoluto.
Come risultato otteniamo un grafico del Mean Squared Error (MSE) per ciascun metodo rispetto al numero di stimatori. Osserviamo che bagging e foreste casuali non migliorano oltre un certo punto, mentre AdaBoost continua ad adattarsi efficacemente.
Importazione delle librerie
Come sempre, iniziamo importando le librerie e le funzioni Python necessarie. Per questo script utilizziamo diversi moduli di Scikit-Learn. Inoltre includiamo i pacchetti fondamentali come Matplotlib, NumPy, Pandas e Seaborn per analisi e visualizzazione dei dati. Ci serviamo anche dei metodi ensemble di decision tree come BaggingRegressor, RandomForestRegressor e AdaBoostRegressor.
Infine, importiamo la metrica mean_squared_error, la funzione train_test_split per la divisione dei dati, i tool di preprocessing e il DecisionTreeRegressor.
# ensemble_prediction.py
import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yfinance as yf
import seaborn as sns
import sklearn
from sklearn.ensemble import (
BaggingRegressor, RandomForestRegressor, AdaBoostRegressor
)
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import scale
from sklearn.tree import DecisionTreeRegressor
Acquisizione serie finanziarie
Prima di tutto dobbiamo usare Pandas per creare il DataFrame dei valori ritardati. Questo particolare pezzo di codice è stato ampiamente utilizzato in altri articoli sul sito, quindi non c’è bisogno di descriverlo nei dettagli. La funzione crea un DataFrame contenente i dati dei rendimenti ritardati di tre giorni per una specifica serie temporale di un asset disponibile su Yahoo Finance (oltre al volume degli scambi giornalieri):
def create_lagged_series(symbol, start_date, end_date, lags=3):
"""
Crea un DataFrame panda che memorizza
i rendimenti percentuali dell valore della chiusura
rettificata di un assest scaricato da Yahoo Finance,
insieme a una serie di rendimenti ritardati dei
giorni di trading precedenti (il ritardo predefinito è 3 giorni).
È incluso anche il volume degli scambi.
"""
# Scaricare i dati storici da Yahoo Finance
ts = yf.download(symbol, start=start_date, end=end_date, group_by='ticker', auto_adjust=False)
ts = ts[symbol]
# Creazione di un DataFrame dei ritardi
tslag = pd.DataFrame(index=ts.index)
tslag["Today"] = ts["Adj Close"]
tslag["Volume"] = ts["Volume"]
# Creazione della serie dei ritardi dei
# prezzi di chiusura dei giorni precedenti
for i in range(0,lags):
tslag["Lag%s" % str(i+1)] = ts["Adj Close"].shift(i+1)
# Creazione del DataFrame dei rendimenti
tsret = pd.DataFrame(index=tslag.index)
tsret["Volume"] = tslag["Volume"]
tsret["Today"] = tslag["Today"].pct_change()*100.0
# Creazione delle colonne delle percentuali dei rendimenti ritardi
for i in range(0,lags):
tsret["Lag%s" % str(i+1)] = tslag[
"Lag%s" % str(i+1)
].pct_change()*100.0
tsret = tsret[tsret.index >= start_date]
return tsret
Preparazione dei dati
Nella funzione __main__ impostiamo i parametri. Innanzitutto definiamo un seme casuale per rendere il codice replicabile su altri ambienti di lavoro. Il parametro n_jobs controlla il numero dei core del processore da utilizzare per il bagging e per le foreste casuali. Il boosting non è parallelizzabile, quindi non fa uso di questo parametro.
Il parametro n_estimators definisce il numero totale di stimatori da utilizzare nel grafico del MSE, mentre step_factor controlla la granularità del calcolo impostando i passi attraverso il numero di stimatori. In questo caso axis_step è uguale a 1000/10 = 100, cioè sono eseguiti 100 calcoli separati per ciascuno dei tre metodi di ensemble:
# Impostazione del seed random, numero di stimatori
# and lo "step factor" usato per il grafico di MSE
# per ogni metodo
random_state = 42
n_jobs = 1 # Fattore di parallelizazione per il bagging e random forests
n_estimators = 1000
step_factor = 10
axis_step = int(n_estimators/step_factor)
Il codice seguente scarica dieci anni di prezzi AMZN e li converte in una serie dei rendimenti lagged utilizzando la funzione create_lagged_series. I valori mancanti vengono eliminati (una conseguenza della procedura di calcolo dei ritardi) e i dati vengono ridimensionati in modo che siano compresi tra -1 e +1 per facilitare il confronto.
Quest’ultima procedura è comune nel machine learning e permette alle feature con grandi differenze nelle dimensioni assolute di essere paragonabili ai modelli:
# Scaricare 10 anni di storico di Amazon
start = datetime.datetime(2006, 1, 1)
end = datetime.datetime(2015, 12, 31)
amzn = create_lagged_series("AMZN", start, end, lags=3)
amzn.dropna(inplace=True)
# Uso dei ritardi dei primi 3 giorni dei prezzi close di AMZN
# e ridimensione dei dati ttra -1 e +1 per i confronti
X = amzn[["Lag1", "Lag2", "Lag3"]]
y = amzn["Today"]
X = scale(X)
y = scale(y)
I dati sono suddivisi in un set di addestramento e un set di test, con il 70% dei dati che formano i dati di addestramento e il restante 30% che formano il set di test.
Da sottolineare che le serie temporali di dati finanziari hanno correlazione seriale, quindi questa procedura introduce alcuni errori dato che non teniamo di questa correlazione. Tuttavia, è trascurabile nel confronto tra i tre metodi d’insieme, scopo principale di questo articolo:
# Divisione in training-testing con il 70% dei dati per il
# training e il rimanente 30% dei dati per il testing
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=random_state
)
Applicazione dei metodi
Le seguenti matrici NumPy memorizzano il numero di stimatori a ogni step dell’asse, nonché l’effettivo MSE associato per ciascuno dei tre metodi dell’insieme. Sono tutti inizialmente azzerati e successivamente compilati:
# Inizializzazione degli array che conterrano il
# MSE per ogni metodo d'insieme
estimators = np.zeros(axis_step)
bagging_mse = np.zeros(axis_step)
rf_mse = np.zeros(axis_step)
boosting_mse = np.zeros(axis_step)
Il primo metodo di ensemble di decision tree da utilizzare è la procedura di bagging. Il codice esegue un’iterazione sul numero totale di stimatori (in questo caso da 1 a 1000, con un passo di dimensione pari a 10), definisce il modello dell’insieme con il corretto modello di base (in questo caso un Decision Tree di regressione), lo adatta ai dati di addestramento e quindi calcola l’errore quadratico medio sui dati del test. Questo MSE viene quindi aggiunto all’array del bagging MSE:
# Stimare il Bagging MSE per l'intero numero di
# stimatore, con un passo specifico ("step_factor")
for i in range(0, axis_step):
print("Bagging Estimator: %d of %d..." % (
step_factor * (i + 1), n_estimators)
)
bagging = BaggingRegressor(
DecisionTreeRegressor(),
n_estimators=step_factor * (i + 1),
n_jobs=n_jobs,
random_state=random_state
)
bagging.fit(X_train, y_train)
mse = mean_squared_error(y_test, bagging.predict(X_test))
estimators[i] = step_factor * (i + 1)
bagging_mse[i] = mse
Lo stesso approccio viene eseguito per le random forest. Poiché le foreste casuali utilizzano implicitamente un albero di regressione come stimatore di base, non è necessario specificarlo nel costruttore dell’insieme:
# Stima del Random Forest MSE per l'intero numero di
# stimatori, con un passo specifico ("step_factor")
for i in range(0, axis_step):
print("Random Forest Estimator: %d of %d..." % (
step_factor * (i + 1), n_estimators)
)
rf = RandomForestRegressor(
n_estimators=step_factor * (i + 1),
n_jobs=n_jobs,
random_state=random_state
)
rf.fit(X_train, y_train)
mse = mean_squared_error(y_test, rf.predict(X_test))
estimators[i] = step_factor * (i + 1)
rf_mse[i] = mse
Allo stesso modo per l’algoritmo di boosting AdaBoost sebbene non è presente il parametro n_jobs perchè le tecniche di boosting non sono parallelizzabili. Il tasso di apprendimento, o fattore di contrazione, \lambda è stato impostato a 0,01. La regolazione di questo valore ha un grande impatto sull’assoluto MSE calcolato per ciascun stimatore totale:
# Stima del AdaBoost MSE per l'intero numero di
# stimatori, con un passo specifico ("step_factor")
for i in range(0, axis_step):
print("Boosting Estimator: %d of %d..." % (
step_factor * (i + 1), n_estimators)
)
boosting = AdaBoostRegressor(
DecisionTreeRegressor(),
n_estimators=step_factor * (i + 1),
random_state=random_state,
learning_rate=0.01
)
boosting.fit(X_train, y_train)
mse = mean_squared_error(y_test, boosting.predict(X_test))
estimators[i] = step_factor * (i + 1)
boosting_mse[i] = mse
Risultati
L’ultimo pezzo di codice grafica semplicemente questi array l’uno contro l’altro usando Matplotlib, ma con la combinazione di colori predefinita di Seaborn, che è visivamente più gradevole rispetto ai valori predefiniti di Matplotlib:
# Visualizzazione del grafico del MSE per il numero di stimatori
plt.figure(figsize=(8, 8))
plt.title('Bagging, Random Forest and Boosting comparison')
plt.plot(estimators, bagging_mse, 'b-', color="black", label='Bagging')
plt.plot(estimators, rf_mse, 'b-', color="blue", label='Random Forest')
plt.plot(estimators, boosting_mse, 'b-', color="red", label='AdaBoost')
plt.legend(loc='upper right')
plt.xlabel('Estimators')
plt.ylabel('Mean Squared Error')
plt.show()
Il grafico risultante è riportato nella figura seguente. Da notare come l’aumento del numero di stimatori per i metodi di ensemble di decision tree basati sul bootstrap (bagging e foreste casuali) porta l’MSE a “sistemarsi” e diventare quasi identico tra di loro. Tuttavia, per l’algoritmo di potenziamento AdaBoost si può vedere che l’aumento del numero di stimatori oltre a circa 100, il metodo inizia ad aver un significativo overfit.
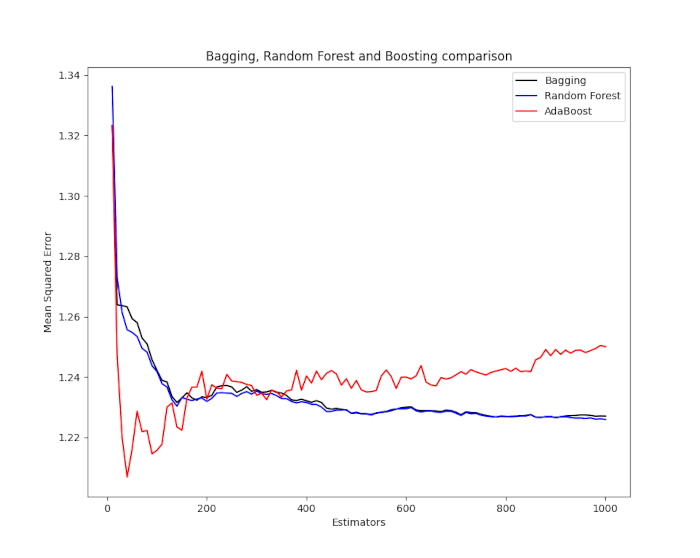
Quando costruiamo una strategia di trading basata su una procedura di boosting ensemble, dobbiamo tenere presente questo aspetto. In caso contrario, rischiamo di ottenere una significativa sottoperformance della strategia quando la applichiamo a dati finanziari fuori campione.
Conclusioni
In questa lezione approfondiamo l’uso dei metodi per l’ensemble di decision tree, concentrandoci in particolare su bagging, random forest e boosting. Spieghiamo come la combinazione di più alberi decisionali, tramite tecniche come il bootstrap e l’aggregazione dei modelli, riduca in modo significativo la varianza delle previsioni e migliori l’accuratezza complessiva.
Con il bagging generiamo modelli paralleli su set bootstrap differenti, mentre le foreste casuali aggiungono una selezione casuale delle feature per ridurre ulteriormente la correlazione tra gli alberi. Il boosting, invece, costruisce i modelli in sequenza e corregge progressivamente gli errori dei modelli precedenti.
Mettiamo in evidenza anche le differenze pratiche tra i tre approcci: il bagging e le random forest si prestano bene alla parallelizzazione, mentre il boosting, essendo sequenziale, richiede più risorse computazionali ma spesso risulta più preciso. Infine, implementiamo questi algoritmi in Python con Scikit-Learn, utilizzando dati reali di mercato per prevedere i rendimenti azionari. I risultati mostrano chiaramente come ogni tecnica offra vantaggi specifici in termini di errore medio quadratico, e sottolineano l’importanza di scegliere l’algoritmo in base sia alle caratteristiche del dataset sia agli obiettivi del modello.
Nelle prossime lezioni, applicheremo queste tecniche a strategie di trading quantitativo più avanzate.
Riferimenti
- [1] Efron, B. (1979) “Bootstrap methods: Another look at the jackknife”, The Annals of Statistics 7 (1): 1-26
- [2] James, G., Witten, D., Hastie, T., Tibshirani, R. (2013) An Introduction to Statistical Learning, Springer
- [3] Wikipedia (2016) Wikipedia: Random Forest, https://en.wikipedia.org/wiki/Random_forest
- [4] Breiman, L. (1996) “Bagging predictors”, Machine Learning 24 (2): 123-140
- [5] Breiman, L. (2001) “Random Forests”, Machine Learning 45 (1): 5-32
- [6] Kearns, M., Valiant, L. (1989) “Crytographic limitations on learning Boolean formulae and finite automata”, Symposium on Theory of computing. ACM. 21 (None): 433-444
- [7] Hastie, T., Tibshirani, R., Friedman, J. (2009) The Elements of Statistical Learning, Springer
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“