In questa prima lezione del corso su gli algoritmi di machine learning supervisionato introduciamo una tecnica di machine learning estremamente potente: la Support Vector Machine (SVM). Consideriamo questa tecnica tra le migliori soluzioni di classificazione supervisionata “pronte all’uso”. Per questo motivo, rappresenta uno strumento fondamentale per chi si occupa di trading quantitativo e per chi lavora come data scientist.
Introduzione al Support Vector Machine
Noi ricercatori quantistici e data scientist dobbiamo sentirci a nostro agio sia con la teoria sia con l’applicazione pratica degli strumenti presenti nella nostra cassetta degli attrezzi. Per questo motivo, iniziamo con questa lezione una serie dedicata alle Support Vector Machine. In particolare, oggi descriviamo la teoria dei maximal margin classifier, support vector classifier e delle support vector machine. Nelle prossime lezioni utilizzeremo la libreria scikit-learn di Python per mostrare alcuni esempi pratici di queste tecniche teoriche su dati reali.
Come accade per ogni classificatore binario supervisionato, il compito di una Support Vector Machine consiste nel trovare un confine di separazione (lineare o non lineare) all’interno di uno spazio di elementi, così da poter classificare automaticamente le osservazioni future in gruppi distinti. Un ottimo esempio è la classificazione di documenti in base al sentiment positivo o negativo. Allo stesso modo, possiamo distinguere e-mail spam da quelle legittime. Le Support Vector Machine SVM si adattano perfettamente a questi scenari.
Procediamo analizzando il concetto di iperpiano di separazione ottimale, un classificatore lineare semplice noto come maximal margin classifier. Dimostriamo che spesso questo tipo di classificatore non funziona bene nei casi complessi del mondo reale e, per questo motivo, introduciamo il support vector classifier (SVC), che supera il vincolo della linearità. Infine, esploriamo le support vector machines non lineari, che usano le funzioni del kernel per aumentare l’efficienza computazionale.
Iperpiano di Separazione Ottimale
Prima di approfondire il funzionamento dei classificatori SVC e delle support vector machine SVM, definiamo il concetto di iperpiano di separazione ottimale (OSH).
Consideriamo uno spazio a valori reali di dimensione p (ad esempio \mathbb{R}^p). L’iperpiano di separazione ottimale corrisponde a uno spazio affine di dimensione p-1 che risiede nello spazio più ampio p-dimensionale. Più avanti spiegheremo cosa rende “ottimale” questa separazione.
Nel caso p=2, questo spazio affine è una semplice retta; per p=3, diventa un piano bidimensionale (vedi Fig. 1 e Fig. 2).

Quando p>3, parliamo di un iperpiano. Sebbene risulti difficile (o impossibile!) da visualizzare, possiamo comprenderne il significato concettualmente.
Ricordiamo che “affine” indica che l’iperpiano non deve necessariamente passare per l’origine dello spazio p-dimensionale.
Se consideriamo un punto nello spazio p-dimensionale, ossia x=(X_1, ..., X_p)\in \mathbb{R}^p, possiamo definire un iperpiano affine di dimensione p-1 con la seguente equazione:
\(\begin{eqnarray} \beta_0 + \beta_1 X_1 + … + \beta_p X_p = 0 \end{eqnarray}\)
oppure in forma compatta:
\(\begin{eqnarray} \beta_0 + \sum^{p}_{j=1} \beta_j X_j = 0 \end{eqnarray}\)
Se un punto x\in\mathbb{R}^p soddisfa questa equazione, allora giace sull’iperpiano di dimensione p-1.
Possiamo anche considerare altri punti x tali che:
\(\begin{eqnarray} \beta_0 + \sum^{p}_{j=1} \beta_j X_j > 0 \end{eqnarray}\)
in questo caso il punto x si trova sopra l’iperpiano, oppure:
\(\begin{eqnarray}\beta_0+\sum^{p}_{j=1}\beta_j X_j <0 \end{eqnarray}\)
e allora il punto x si trova al di sotto dell’iperpiano.
L’iperpiano, quindi, divide lo spazio p-dimensionale in due regioni (vedi Figura 3). Da qui nasce il termine “separazione” nell’espressione “iperpiano di separazione ottimale”. Non abbiamo ancora esplorato cosa rende questa separazione “ottimale”!
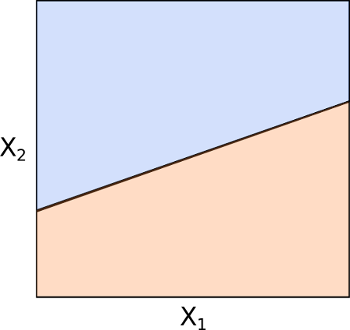
Il punto chiave consiste nella possibilità di stabilire da che parte del piano cadrà un punto \(x\) semplicemente calcolando il segno dell’espressione \(\beta_0+\sum^{p}_{j=1}\beta_j X_j\). Questo concetto rappresenta la base di una tecnica di classificazione supervisionata.
Classificazione
Proseguiamo con l’esempio di filtro delle e-mail spam. Immaginiamo il nostro problema di classificazione come formato da un migliaio di e-mail (\(n=1000\)), ciascuna contrassegnata come spam (\(+1\)) oppure non spam (\(-1\)). A ogni e-mail associamo un insieme di parole chiave (ottenute separando il testo in base agli spazi), che definiamo come features. Se raccogliamo tutte le parole chiave possibili da ogni e-mail (eliminando i duplicati), otteniamo in totale \(p\) parole chiave.
Quando traduciamo questo in termini matematici, impostiamo il problema classico della classificazione supervisionata considerando un insieme di \(n\) osservazioni di addestramento \(x_i\), ciascuna rappresentata da un vettore di dimensione \(p\) che include le features.
Ogni osservazione ha una class label associata \(y_i \in \{-1,1\}\). Quindi, pensiamo a \(n\) coppie \((x_i, y_i)\) che rappresentano le caratteristiche e le etichette di classe (liste di parole chiave e tag spam/non spam). Inoltre, consideriamo anche osservazioni di prova \(x^{*}=(x^{*}_1,…,x^{*}_p)\) che useremo per testare le performance dei classificatori. Queste rappresentano nuove e-mail non ancora esaminate.
Il nostro obiettivo consiste nel costruire un classificatore, basandoci sulle osservazioni di addestramento, che riesca a classificare correttamente le osservazioni di test analizzando solo le caratteristiche in input. Vogliamo quindi determinare se un’e-mail è spam oppure no unicamente osservando le parole chiave che contiene.
All’inizio assumiamo di poter costruire un iperpiano, attraverso un metodo che definiremo in seguito, capace di separare perfettamente i dati di addestramento secondo le etichette di classe (vedi Fig. 4 e 5). Questo significherebbe separare chiaramente le e-mail di spam da quelle non spam usando soltanto parole chiave specifiche.
Il diagramma che segue mostra il caso \(p=2\), ma nel caso reale potremmo avere \(p > 10000\) parole chiave. Quindi, le figure 4 e 5 hanno uno scopo puramente illustrativo.
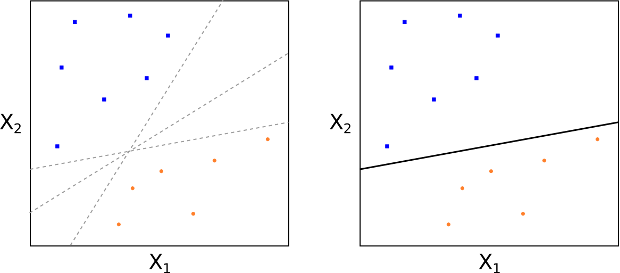
Questa impostazione porta a una proprietà matematica di separazione:
\(\begin{eqnarray} \beta_0 + \beta_1 X_{i1} + … + \beta_p X_{ip} = \beta_0 + \sum^{p}_{j=1} \beta_j X_{ij} > 0\end{eqnarray}\), se \(y_i=1\)
\(\begin{eqnarray} \beta_0 + \beta_1 X_{i1} + … + \beta_p X_{ip} = \beta_0 + \sum^{p}_{j=1} \beta_j X_{ij} < 0\end{eqnarray}\), se \(y_i=-1\)
In altre parole, se ogni osservazione si trova sopra o sotto l’iperpiano di separazione secondo l’equazione geometrica del piano, assegniamo rispettivamente l’etichetta \(+1\) oppure \(-1\). In questo modo, costruiamo (potenzialmente) un processo semplice di classificazione.
Classifichiamo ogni osservazione di prova in base al lato dell’iperpiano in cui cade. Formalizziamo il tutto con la funzione \(f(x)\), valutata su un’osservazione di prova \( x^{*} = (X ^ {*} _ 1, …, X ^ {*} _ p)\):
\(\begin{eqnarray} f(x^{*}) = \beta_0 + \sum^{p}_{j=1} \beta_j X^{*}_j \end{eqnarray}\)
Se \(f(x^{*}) > 0\), allora \(y^{*} = +1\); se invece \(f(x^{*}) < 0\), allora \(y^{*} = -1\).
Possiamo anche valutare l’ampiezza della distanza \(f(x)\). Se \(|f(x^{*})|\) è molto grande, ci sentiamo sicuri dell’etichetta assegnata, perché l’osservazione è distante dall’iperpiano. Se invece \(|f(x^{*})|\) è vicino a zero, significa che il punto è vicino all’iperpiano e la nostra sicurezza nella classificazione diminuisce.
Maximal Margin Classifiers
Non abbiamo ancora spiegato come costruiamo un iperpiano di separazione, né abbiamo chiarito cosa intendiamo con il termine “ottimale”. In generale, possiamo ottenere diversi iperpiani di separazione, poiché possiamo traslarli o ruotarli leggermente senza toccare alcuna osservazione di addestramento (vedi Fig 4).
Come scegliamo allora il “migliore” iperpiano di separazione o quello più “ottimale”? Costruiamo un iperpiano del margine massimo (MMH), ovvero l’iperpiano di separazione più distante da tutte le osservazioni di addestramento.
Come procediamo? Iniziamo calcolando la distanza perpendicolare di ciascuna osservazione di addestramento \(x_i\) rispetto a un iperpiano di separazione. Chiamiamo margine la distanza più piccola tra una di queste osservazioni e l’iperpiano. Il MMH è l’iperpiano che massimizza questa distanza. In questo modo, garantiamo la massima separazione possibile dalle osservazioni di training.
Classificare un’osservazione di prova diventa quindi una semplice questione di determinare da quale lato dell’iperpiano essa cade. Possiamo farlo usando la formula per \(f(x^*)\). Questo tipo di classificatore prende il nome di classificatore del margine massimo (MMC). Speriamo che un margine ampio ottenuto sugli esempi di addestramento si traduca in un margine ampio anche sulle osservazioni di prova, migliorando così la capacità di classificazione.
Prestiamo però attenzione all’overfitting quando lavoriamo con un numero elevato di dimensioni delle feature, come accade spesso nel Natural Language Processing (ad esempio nella classificazione dello spam e-mail). In questi casi, l’MMH potrebbe adattarsi perfettamente ai dati di addestramento, ma comportarsi male quando valutiamo i dati di test.
Il nostro obiettivo con questo algoritmo è calcolare i valori di \(\beta_j\) (cioè determinare la geometria corretta dell’iperpiano), per poi applicare \(f(x^*)\) a qualsiasi osservazione di prova.
Osservando la Fig 6, notiamo che l’MMH rappresenta la linea mediana del “blocco” più ampio che possiamo inserire tra le due classi in modo che risultino perfettamente separate.
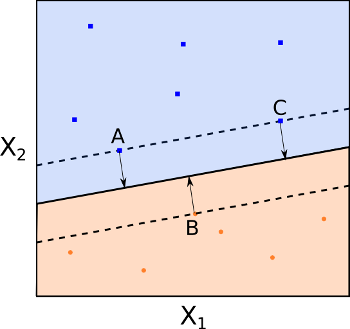
Una caratteristica fondamentale del MMC (e successivamente di SVC e Support Vector Machine SVM) è che la posizione dell’MMH dipende esclusivamente dai vettori di supporto, ossia le osservazioni di addestramento che si trovano esattamente sul margine (ma non sull’iperpiano) (vedi i punti A, B e C della Fig 6). Questo significa che la posizione dell’MMH non cambia al variare delle altre osservazioni di addestramento.
Osserviamo però che un potenziale svantaggio del MMC è la sensibilità del suo MMH alla posizione dei vettori di supporto, con conseguente impatto diretto sulle prestazioni del classificatore.
Costruzione del Maximal Margin Classifier
Troviamo istruttivo delineare completamente il problema di ottimizzazione che dobbiamo risolvere per creare l’MMH (e quindi anche l’MMC). Mentre descriviamo i vincoli del problema di ottimizzazione, specifichiamo che la soluzione algoritmica va oltre lo scopo di questa lezione. Per fortuna, troviamo già implementate queste routine di ottimizzazione nella libreria scikit-learn (tramite la libreria LIBSVM).
Seguiamo questa procedura per determinare un iperpiano del margine massimo in un classificatore del margine massimo. Date n osservazioni di addestramento x_1,…,x_n\in\mathbb{R}^p e n class label y_1,…,y_n\in\{-1,1\}, otteniamo l’MMH come soluzione al seguente problema di ottimizzazione:
Massimizziamo M\in\mathbb{R}, variando \beta_1,…,\beta_p in modo che:
\begin{eqnarray} \sum^{p}_{j=1} \beta^2_j = 1 \end{eqnarray}
\begin{eqnarray} y_i \left( \beta_0 + \sum^{p}_{j=1} \beta_j X_{ij} \right) \geq M, \quad \forall i = 1,…,n \end{eqnarray}
Nonostante i vincoli formali complessi, affermiamo in pratica che ogni osservazione deve trovarsi dal lato corretto dell’iperpiano e almeno a una distanza M da esso. Poiché il nostro obiettivo è massimizzare M, questa rappresenta esattamente la condizione necessaria per costruire l’MMC!
Nel caso ideale, otteniamo una separabilità perfetta. Tuttavia, nella maggior parte dei dataset reali non troviamo una separabilità perfetta con un iperpiano lineare (vedi Fig. 7). Quando non rileviamo separabilità, non possiamo costruire l’MMC seguendo la procedura sopra descritta. Quindi, come creiamo un iperpiano separatore in questi casi?
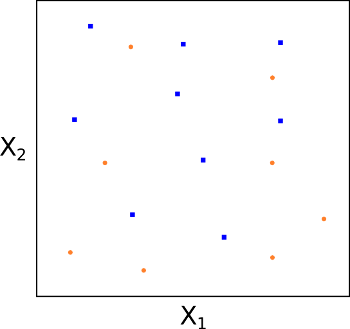
Dobbiamo approssimare il requisito che un iperpiano separi perfettamente ogni osservazione di training sul lato corretto (cioè associandola alla sua vera class label), utilizzando quello che chiamiamo margine morbido. Questo concetto motiva l’introduzione del classificatore di vettori di supporto (SVC) e delle Support Vector Machine (SVM) .
Support Vector Classifiers (SVC)
Come abbiamo già osservato, uno dei limiti dell’MMC è l’eccessiva sensibilità all’aggiunta di nuove osservazioni di training. Osserviamo le figure 8 e 9. Nella figura 8 notiamo che un MMH separa perfettamente le due classi. Tuttavia, nella figura 9, aggiungendo un punto alla classe +1, vediamo che la posizione dell’MMH cambia drasticamente. In questa situazione, l’MMH mostra chiaramente un over-fit.
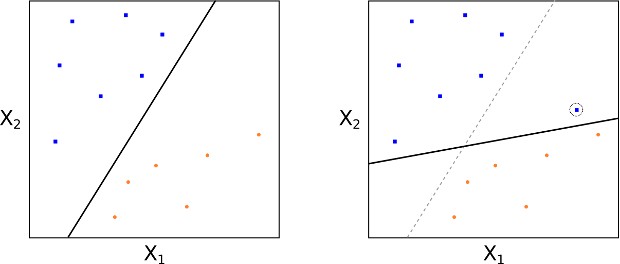
Come anticipato, consideriamo un classificatore basato su un iperpiano separatore che non separa perfettamente le due classi, ma risulta più robusto all’aggiunta di nuove osservazioni individuali e classifica meglio la maggior parte delle osservazioni di training. Accettiamo, in questo caso, alcuni errori di classificazione sulle osservazioni di addestramento.
Un classificatore SVC, o a margine morbido, funziona in questo modo. L’SVC consente ad alcune osservazioni di trovarsi dal lato errato del margine (o dell’iperpiano), offrendo così una separazione “morbida”. Le figure 10 e 11 mostrano osservazioni rispettivamente sul lato sbagliato del margine e dell’iperpiano.
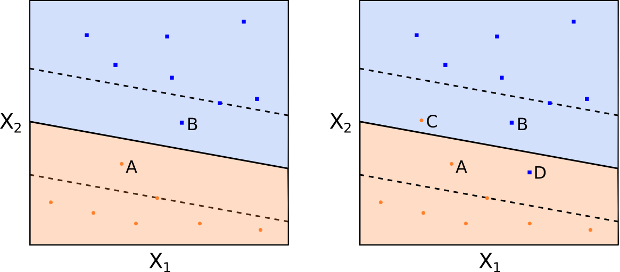
Come prima, classifichiamo un’osservazione in base al lato dell’iperpiano di separazione su cui si trova, ma alcuni punti possono comunque risultare classificati in modo errato.
Risulta istruttivo osservare come la procedura di ottimizzazione si differenzia da quella che abbiamo applicato nella MMC. Introduciamo nuovi parametri, ossia i valori \(n\) \(\epsilon_i\) (noti come valori di slack) e un parametro \(C\), noto come budget. Cerchiamo di massimizzare \(M\), ottimizzando \(\beta_1,…,\beta_p,\epsilon_1,…,\epsilon_n\) affinché:
\(\begin{eqnarray} \sum^{p}_{j=1} \beta^2_j = 1 \end{eqnarray}\)
e
\(\begin{eqnarray} y_i \left( \beta_0 + \sum^{p}_{j=1} \beta_j X_{ij} \right) \geq M, \quad \forall i = 1,…,n \end{eqnarray}\)
e
\(\begin{eqnarray} \epsilon_i \geq 0, \quad \sum^{n}_{i=1} \epsilon_i \leq C \end{eqnarray}\)
Definiamo \(C\), il budget, come un parametro di regolazione non negativo. Il margine è ancora rappresentato da \(M\), mentre le variabili slack \(\epsilon_i\) ci permettono di collocare alcune osservazioni sul lato sbagliato del margine o dell’iperpiano.
In pratica, \(\epsilon_i\) ci indica dove si posiziona l’osservazione \(i\)-esima rispetto al margine e all’iperpiano. Quando \(\epsilon_i = 0\), sappiamo che l’osservazione di addestramento \(x_i\) si trova sul lato corretto del margine. Se \(\epsilon_i > 0\), allora \(x_i\) si posiziona sul lato errato del margine; se \(\epsilon_i > 1\), è dalla parte sbagliata dell’iperpiano.
Utilizziamo \(C\) per controllare quanto possiamo modificare i singoli \(\epsilon_i\) permettendo loro di violare il margine. Impostando \(C = 0\), imponiamo che \(\epsilon_i = 0, \forall i\), escludendo ogni violazione del margine e ottenendo, in caso di classi separabili, la situazione MMC.
Se invece impostiamo \(C > 0\), consentiamo a non più di \(C\) osservazioni di violare l’iperpiano. Con l’aumento di \(C\), cresce anche il margine. Osserviamo le Figure 12 e 13 per vedere due valori diversi di \(C\).
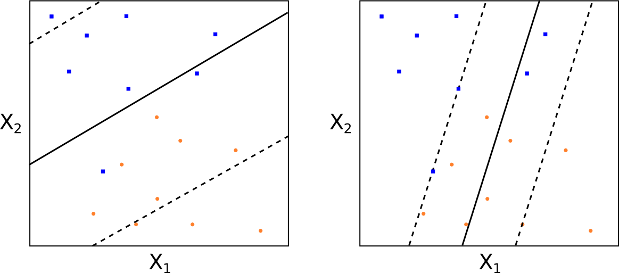
Come scegliamo in pratica \(C\)? Di solito lo selezioniamo tramite convalida incrociata. In sostanza, \(C\) regola il compromesso bias-varianza nella SVC. Un valore piccolo indica basso bias e alta varianza, mentre un valore grande implica alto bias e bassa varianza.
Come prima, per classificare una nuova osservazione di test \(x^{*}\), calcoliamo il segno di \(f(x^{*})=\beta_0 + \sum^{p}_{i = 1} \beta_j X^{*}_j\).
Questo approccio funziona bene per classi separate linearmente (o quasi). Ma cosa accade se i confini di separazione non sono lineari? Come affrontiamo questi casi? È qui che entrano in gioco le macchine a vettore di supporto.
Support Vector Machine
Estendiamo una SVC per ottenere confini decisionali non lineari: questo è il dominio della Support Vector Machine (SVM). Esaminiamo le Figure 14 e 15. In tali casi, una SVC puramente lineare fallisce perché i dati non presentano una chiara separazione lineare.
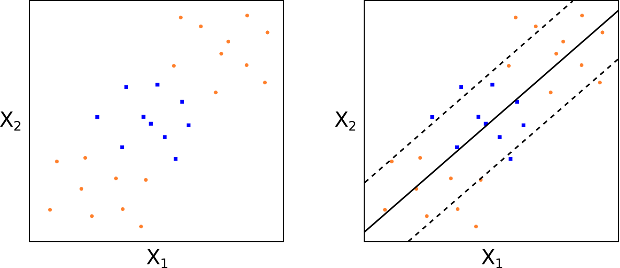
Quindi le SVC non ci servono nei problemi in cui il confine tra le classi risulta altamente non lineare.
Per comprendere come funziona una Support Vector Machine, applichiamo un “trucco” classico della regressione lineare quando affrontiamo situazioni non lineari. In particolare, trasformiamo un insieme di \(p\) caratteristiche \(X_1, …, X_p\) in un insieme di \(2p\) caratteristiche \(X_1, X^2_1, …, X_p, X^2_p\). In questo modo, possiamo usare una tecnica lineare anche su caratteristiche non lineari.
Il confine di decisione resta lineare nel nuovo spazio \(2p\)-dimensionale, ma appare non lineare nello spazio originale \(p\)-dimensionale. Otteniamo così un confine di decisione espresso come \( q(x)=0\), dove \(q\) rappresenta una funzione polinomiale quadratica delle feature originali: otteniamo quindi una soluzione non lineare.
Naturalmente non ci limitiamo ai polinomi quadratici. Possiamo includere anche polinomi di grado superiore, termini di interazione e altre forme funzionali. Tuttavia, espandere così lo spazio delle feature può far crescere la complessità al punto da rendere alcuni algoritmi ingestibili.
Con le Support Vector Machine, estendiamo lo spazio delle funzionalità in modo non lineare, ma manteniamo l’efficienza computazionale grazie al metodo kernel, che descriveremo tra poco.
Ma cosa sono in realtà gli SVM? In pratica, estendiamo le SVC espandendo lo spazio delle feature con funzioni chiamate kernel. Per capire i kernel, esploriamo brevemente alcuni aspetti legati alla soluzione del problema di ottimizzazione delle SVC.
Durante la risoluzione di questo problema, l’algoritmo utilizza solo prodotti interni tra le osservazioni e tra ciascuna osservazione e se stessa. Ricordiamo che, per due vettori \(p\)-dimensionali \(u, v\), il prodotto interno è:
\(\begin{eqnarray} \langle u,v \rangle = \sum^{p}_{i=1} u_i v_i \end{eqnarray}\)
E per due osservazioni otteniamo:
\(\begin{eqnarray} \langle x_i,x_k \rangle = \sum^{p}_{j=1} x_{ij} x_{kj} \end{eqnarray}\)
Pur evitando i dettagli tecnici (non necessari per questa lezione), possiamo mostrare che un classificatore lineare a vettori di supporto per un’osservazione \(x\) si esprime come combinazione lineare di prodotti interni:
\(\begin{eqnarray} f(x) = \beta_0 + \sum^{n}_{i=1} \alpha_i \langle x, x_i \rangle \end{eqnarray}\)
Con \(n\) e \(\alpha_i\) che rappresentano i coefficienti associati a ciascuna osservazione di addestramento.
Per stimare i coefficienti \(\beta_0\) e \(\alpha_i\), calcoliamo \({n \choose 2} = n(n-1)/2\) prodotti interni tra tutte le coppie di osservazioni. In pratica, ci limitiamo a calcolare i prodotti interni per il sottoinsieme delle osservazioni che fungono da vettori di supporto. Indichiamo questo sottoinsieme come \(\mathscr{S}\), quindi:
\(\begin{eqnarray} \alpha_i = 0 \enspace \text{if} \enspace x_i \notin \mathscr{S} \end{eqnarray}\)
Riscriviamo così la formula:
\(\begin{eqnarray} f(x) = \beta_0 + \sum_{i \in \mathscr{S}} \alpha_i \langle x, x_i \rangle \end{eqnarray}\)
Questa forma ci garantisce un vantaggio importante in termini di efficienza computazionale.
Qui nasce la motivazione per estendere le SVC in Support Vector Machine SVM. Sostituendo il prodotto interno \(\langle x_i, x_k \rangle\) con una funzione kernel più generale \(K = K(x_i, x_k)\), trasformiamo la rappresentazione della SVC per utilizzare funzioni non lineari del kernel e ridefiniamo la misura di “somiglianza” tra due osservazioni. Ad esempio, per riprodurre l’SVC, impostiamo \(K\) così:
\(\begin{eqnarray} K(x_i, x_k) = \sum^{p}_{j=1} x_{ij} x_{kj} \end{eqnarray}\)
Poiché questo kernel è lineare rispetto alle caratteristiche, chiamiamo il modello SVC lineare. Possiamo anche adottare kernel polinomiali di grado \(d\), come segue:
\(\begin{eqnarray} K(x_i, x_k) = (1 + \sum^{p}_{j=1} x_{ij} x_{kj})^d \end{eqnarray}\)
Con questa scelta otteniamo un confine decisionale molto più flessibile, che equivale ad applicare una SVC in uno spazio di dimensione superiore formato da polinomi di grado \(d\) delle caratteristiche (vedi la Figura 16).
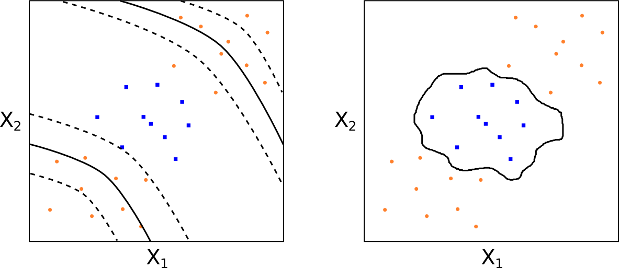
Dunque, definiamo una macchina a vettori di supporto come una SVC che impiega un kernel non lineare. Un kernel ampiamente utilizzato è il kernel radiale (vedi Fig. 17):
\(\begin{eqnarray} K(x_i, x_k) = \exp \left(-\gamma \sum^{p}_{j=1} (x_{ij} – x_{kj})^2 \right), \quad \gamma > 0 \end{eqnarray}\)
Ma come funzionano i kernel radiali? Rispetto ai kernel polinomiali, mostrano un comportamento molto diverso. Se la nostra osservazione di test \(x^{*}\) risulta distante dall’osservazione di addestramento \(x_i\), secondo la distanza euclidea standard, allora la somma \(\sum^{p}_{j=1} (x^{*}_j-x_{ij})^2\) sarà grande, e \(K(x^{*}, x_i)\) assumerà un valore molto piccolo. Di conseguenza, \(x_i\) influenzerà appena la posizione di \(x^{*}\) nella funzione \(f(x^{*})\).
Questo ci mostra come il kernel radiale agisca in modo estremamente localizzato: solo le osservazioni di addestramento vicine a \(x^{*}\) influenzano la sua classificazione.
Conclusioni
Per mettere in pratica la teoria delle Support Vector Machine che abbiamo esplorato, nelle prossime lezioni realizzeremo classificazioni di esempio utilizzando la libreria Python scikit-learn.

