In questa lezione, però, introduciamo il modello a media mobile di ordine q, noto come MA(q). Il Modello a media mobile (MA) rappresenta un componente del più generale modello ARMA, e dobbiamo comprenderlo bene prima di procedere.
Nella precedente lezione descriviamo il modello autoregressivo di ordine p, noto anche come modello AR(p). Lo introduciamo come un’estensione del modello della random walk, con l’obiettivo di spiegare la correlazione seriale aggiuntiva nelle serie temporali finanziarie.
Alla fine comprendiamo che questo approccio non riesce a catturare completamente l’autocorrelazione presente nelle serie temporali finanziarie. Questo accade principalmente perché gli asset finanziari presentano eteroschedasticità condizionale, ossia non risultano stazionari e attraversano fasi di “varianza variabile” o clustering di volatilità, che il modello AR(p) non riesce a considerare.
Nelle prossime lezioni approfondiamo i modelli ARIMA (Autoregressive Integrated Moving Average), insieme ai modelli eteroschedastici condizionali delle famiglie ARCH e GARCH. Questi modelli ci aiutano a compiere i primi tentativi realistici di prevedere i prezzi degli asset.
Modello a Media Mobile (MA) di ordine q
Fondamento logico
Un modello a media mobile (MA) si avvicina concettualmente al modello autoregressivo, ma invece di combinare linearmente i valori passati della serie temporale, combina linearmente i termini passati del rumore bianco.
In pratica, questo significa che il modello MA utilizza direttamente gli “shock” casuali del rumore bianco per determinare ogni valore attuale. Al contrario, un modello AR(p) considera questi “shock” solo indirettamente tramite la regressione ai valori passati della serie.
Una differenza fondamentale consiste nel fatto che il modello a media mobile (MA) prende in considerazione solo gli ultimi “q” shock per ogni specifico modello MA(q), mentre il modello AR(p) include tutti gli shock passati, anche se con importanza decrescente.
Definizione
Modello a media mobile dell’ordine q
Consideriamo un modello di serie storica \(\{x_t\}\) come un modello a media mobile di ordine q, MA(q), se:
\(\begin{eqnarray}x_t = w_t + \beta_1 w_{t-1} + \ldots + \beta_q w_{t-q}\end{eqnarray}\)
Dove \(\{ w_t \}\) rappresenta il rumore bianco, con \(E(w_t) = 0\) e varianza \(\sigma^2\).
Applicando l’operatore di spostamento all’indietro, B (come spiegato nella lezione precedente), possiamo riscrivere il modello come funzione \(\phi\) di B:
\(\begin{eqnarray} x_t = (1 + \beta_1 {\bf B} + \beta_2 {\bf B}^2 + \ldots + \beta_q {\bf B}^q) w_t = \phi_q ({\bf B}) w_t \end{eqnarray}\)
Utilizziamo la funzione \(\phi\) anche nelle prossime lezioni.
Proprietà del secondo ordine
Come nel modello AR(p), anche nel modello MA(q) la media del processo è pari a zero. Questo perché otteniamo la media sommando le medie dei termini del rumore bianco, che risultano tutti uguali a zero.
\(\begin{eqnarray}\text{Media:} \enspace \mu_x = E(x_t) = \sum^{q}_{i=0} E(w_i) = 0 \end{eqnarray}\)
\(\begin{eqnarray} \text{Varianza:} \enspace \sigma^2_w (1 + \beta^2_1 + \ldots + \beta^2_q) \end{eqnarray}\)
\(\text{ACF:} \enspace \rho_k = \left\{\begin{aligned} &1 && \text{if} \enspace k = 0 \\ &\sum^{q-k}_{i=0} \beta_i \beta_{i+k} / \sum^q_{i=0} \beta^2_i && \text{if} \enspace k = 1, \ldots, q \\ &0 && \text{if} \enspace k > q \end{aligned} \right.\)
Dove \(\beta_0 = 1\)
Ora generiamo alcuni dati simulati e li utilizziamo per costruire i correlogrammi. In questo modo rendiamo la formula precedente più concreta.
Simulazioni e Correlogrammi
MA(1)
Iniziamo con un processo MA(1). Se consideriamo \(\beta_1 = 0.6\) si ha il seguente modello a media mobile (MA):
\(\begin{eqnarray} x_t = w_t + 0.6 w_{t-1} \end{eqnarray}\)
In modo analogo ai modelli AR(p), possiamo usare la libreria Statsmodels di Python per simulare tale serie e quindi tracciare il correlogramma. Dato che abbiamo descritto questo approccio nella precedente lezione sull’analisi delle serie temporali per la visualizzazione dei grafici, riportiamo l’intero codice, anziché dividerlo:
import numpy as np
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
# Imposta il seed per la riproducibilità
np.random.seed(1)
N = 100
# Genera 100 rumori bianchi standard
w = np.random.normal(size=N)
# Inizializza la serie AR(1)
x = np.zeros(N)
for t in range(1, N):
x[t] = w[t] + 0.6 * w[t - 1]
# Grafico modello AR
plt.plot(x)
# Grafico Autocorrelazione
plot_acf(x, lags=30)
plt.show()
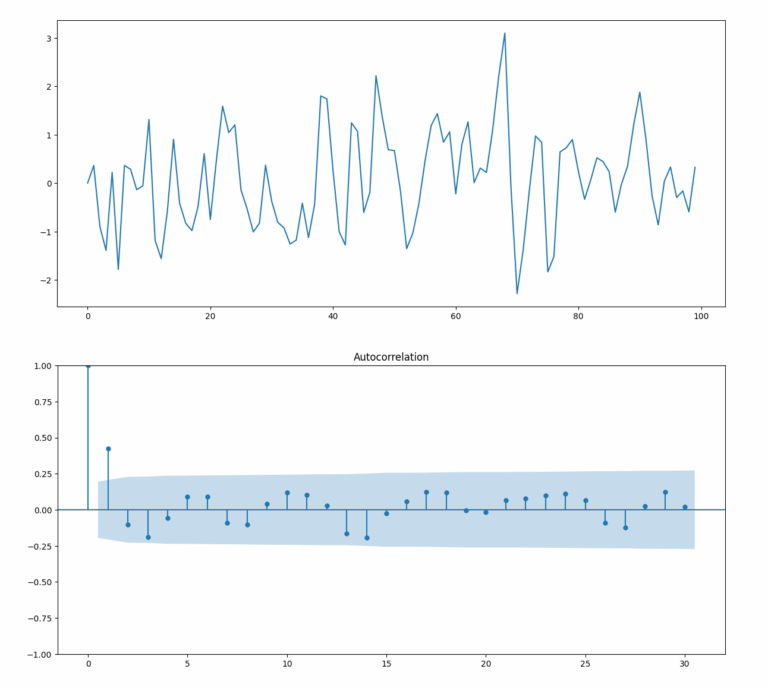
Come descritto in precedenza nella formula di \(\rho_k\), per \(k > q\), tutte le autocorrelazioni dovrebbero essere zero. Con \(q = 1\), dovremmo vedere un picco significativo a \(k=1\) e poi picchi successivi poco significativi. Tuttavia, a causa della distorsione del campionamento, dovremmo aspettarci di vedere picchi (marginalmente) significativi del 5% su un grafico di autocorrelazione del campione.
Questo è esattamente ciò che il correlogramma ci mostra in questo caso. Abbiamo un picco significativo per \(k=1\) e poi picchi insignificanti per \(k>1\).
In effetti, questo è un modo utile per vedere se un modello a media mobile (MA) di ordine q è appropriato. Dando un’occhiata al correlogramma di una particolare serie possiamo vedere quanti ritardi sequenziali diversi da zero esistono. Se esistono tali ritardi possiamo legittimamente tentare di adattare un modello MA(q) a una particolare serie. Poiché disponiamo di prove dai nostri dati simulati di un processo MA(1), possiamo provare a adattare un modello MA(1) ai nostri dati simulati.
Adattare il modello
Sfortunatamente in Python non esiste un comando specifico per i modelli MA come ar lo è per i modelli AR. Tuttavia, possiamo usare la funzione generale ARIMA impostando a zero i parametri autoregressivi e di integrazione.
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(x, order=(0, 0, 1))
result = model.fit()
print(result.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: ARIMA(0, 0, 1) Log Likelihood -127.280
Date: AIC 260.560
Time: 12:06:28 BIC 268.376
Sample: 0 HQIC 263.724
- 100
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0790 0.135 0.584 0.559 -0.186 0.344
ma.L1 0.5554 0.079 7.047 0.000 0.401 0.710
sigma2 0.7438 0.106 7.040 0.000 0.537 0.951
===================================================================================
Ljung-Box (L1) (Q): 0.14 Jarque-Bera (JB): 0.00
Prob(Q): 0.71 Prob(JB): 1.00
Heteroskedasticity (H): 0.87 Skew: 0.01
Prob(H) (two-sided): 0.70 Kurtosis: 3.01
===================================================================================
Il report prodotto dalla funzione ARIMA contiene molte informazioni utili. In primo luogo, possiamo vedere che il parametro è stato stimato come \(\hat{\beta_1} = 0.555\), che è molto vicino al valore reale di \(\hat{\beta_1} = 0.6\). In secondo luogo, gli errori standard sono già calcolati per noi, rendendo semplice il calcolo degli intervalli di confidenza. In terzo luogo, riceviamo una varianza stimata, una probabilità logaritmica e un criterio di informazione Akaike (necessario per il confronto del modello).
La differenza principale tra ARIMA e AR è che ARIMA stima anche un termine di intercetta perché non sottrae la media della serie. Dobbiamo quindi fare attenzione quando effettuiamo previsioni.
Come controllo rapido, possiamo calcolare l’intervallo di confidenza al 95% per \(\hat{\beta_1}\):
phi_hat = result.params[1]
print(phi_hat)
se = result.bse[1]
print(se)
conf_int = phi_hat + np.array([-1.96, 1.96]) * se
print(conf_int)
0.5553989481231544
0.07880878947659437
[0.40093372 0.70986418]
Possiamo vedere che l’intervallo di confidenza al 95% contiene il valore del parametro vero
e quindi possiamo giudicare il modello a media mobile (MA) adatto. Ovviamente questo corrisponde a quanto previsto poiché abbiamo simulato i dati di partenza!
MA(1) con parametro negativo
Come cambiano le cose se modifichiamo il segno di \({\beta_1}\) a -0,6? Eseguiamo la stessa analisi:
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
np.random.seed(1)
w = np.random.normal(size=100)
x = np.zeros(100)
]
for t in range(1, 100):
x[t] = w[t] - 0.6 * w[t-1]
plt.plot(x)
plot_acf(x)
plt.show()
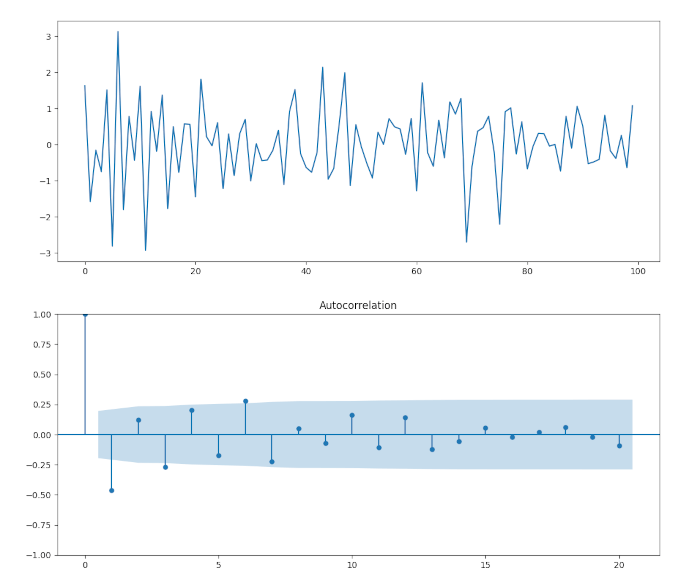
Da notare che per k=1 abbiamo un picco significativo nel correlogramma, che mostra una correlazione negativa, come ci si aspetterebbe da un modello MA(1) con primo coefficiente negativo. Ancora una volta tutti i picchi successivi a K=1 non sono significativi.
Come in precedenza, ora adattiamo un modello MA(1) e stimiamo il parametro tramite la funzione ARIMA:
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(x, order=(0, 0, 1))
result = model.fit()
print(result.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: ARIMA(0, 0, 1) Log Likelihood -130.454
Date: AIC 266.908
Time: 15:27:36 BIC 274.723
Sample: 0 HQIC 270.071
- 100
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0159 0.033 0.475 0.635 -0.050 0.082
ma.L1 -0.6374 0.069 -9.209 0.000 -0.773 -0.502
sigma2 0.7913 0.111 7.121 0.000 0.574 1.009
===================================================================================
Ljung-Box (L1) (Q): 0.14 Jarque-Bera (JB): 0.03
Prob(Q): 0.70 Prob(JB): 0.98
Heteroskedasticity (H): 0.70 Skew: -0.04
Prob(H) (two-sided): 0.31 Kurtosis: 3.03
===================================================================================
Il parametro stimato è \(\hat{\phi}_1 = -0.730\), una lieve sottostima rispetto al valore vero \(\phi_1 = -0.6\).
Calcoliamo infine l’intervallo di confidenza al 95%:
phi_hat = result.params[1]
print(phi_hat)
se = result.bse[1]
print(se)
conf_int = phi_hat + np.array([-1.96, 1.96]) * se
print(conf_int)
-0.6373516046624851
0.06920610801118955
[-0.77299558 -0.50170763]
Possiamo vedere che il valore vero \(\phi_1 = -0.6\) è contenuto nell’intervallo di confidenza al 95%, confermando così che il modello a media mobile (MA) si adatta bene ai dati.
MA(3)
Eseguiamo la stessa procedura per un processo MA(3). Questa volta dovremmo aspettarci picchi significativi per \(k \in \{1,2,3 \}\), e picchi insignificanti per \(k > 3\).
Utilizzeremo i seguenti coefficienti: \(\beta_1 = 0.6\), \(\beta_1 = 0.4\) e \(\beta_1 = 0.2\). Simuliamo un processo MA(3) di questo modello. Per questa simulazione abbiamo aumentato il numero di campioni casuali a 1000, il che rende più facile vedere la vera struttura di autocorrelazione, a scapito di rendere più difficile interpretare la serie originale:
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
np.random.seed(3)
n = 1000
w = np.random.normal(size=n)
x = w.copy()
for t in range(3, n):
x[t] = w[t] + 0.6*w[t-1] + 0.4*w[t-2] + 0.3*w[t-3]
plt.plot(x)
plot_acf(x)
plt.show()
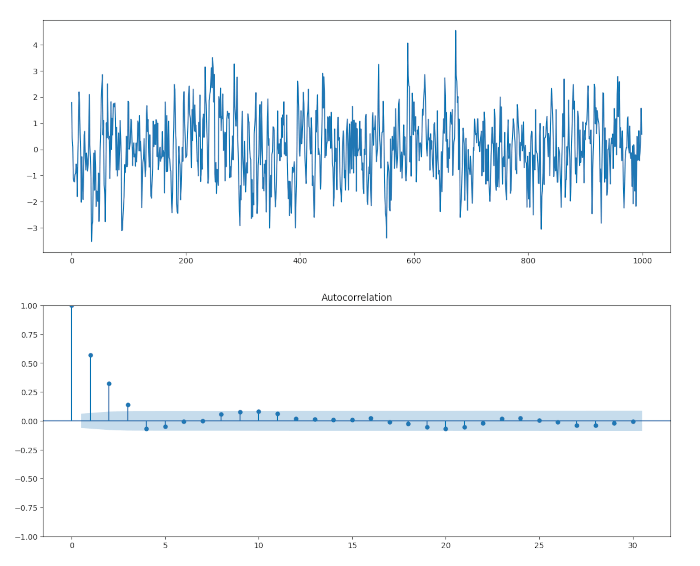
Come previsto, i primi tre picchi sono significativi. Tuttavia, lo è anche il quarto. Ma possiamo legittimamente suggerire che ciò potrebbe essere dovuto ad un bias di campionamento poiché prevediamo che il 5% dei picchi sia significativo oltre \(k=q\).
Adattiamo ora un modello MA(3) ai dati per provare a stimare i parametri:
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(x, order=(0, 0, 3))
result = model.fit()
print(result.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARIMA(0, 0, 3) Log Likelihood -1425.800
Date: AIC 2861.601
Time: 15:55:18 BIC 2886.139
Sample: 0 HQIC 2870.927
- 1000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0400 0.073 0.546 0.585 -0.104 0.184
ma.L1 0.5880 0.031 18.850 0.000 0.527 0.649
ma.L2 0.4117 0.034 12.024 0.000 0.345 0.479
ma.L3 0.3045 0.031 9.751 0.000 0.243 0.366
sigma2 1.0132 0.046 21.914 0.000 0.923 1.104
===================================================================================
Ljung-Box (L1) (Q): 0.06 Jarque-Bera (JB): 0.22
Prob(Q): 0.80 Prob(JB): 0.90
Heteroskedasticity (H): 0.95 Skew: -0.00
Prob(H) (two-sided): 0.67 Kurtosis: 2.93
===================================================================================
# Estrazione dei parametri e degli errori standard
params = result.params
stderr = result.bse
# Intervalli di confidenza al 95% per i parametri MA
conf_int_theta1 = params[1] + np.array([-1.96, 1.96]) * stderr[1]
conf_int_theta2 = params[2] + np.array([-1.96, 1.96]) * stderr[2]
conf_int_theta3 = params[3] + np.array([-1.96, 1.96]) * stderr[3]
print("IC 95% θ1:", conf_int_theta1)
print("IC 95% θ2:", conf_int_theta2)
print("IC 95% θ3:", conf_int_theta3)
IC 95% θ1: [0.52686518 0.64914585]
IC 95% θ2: [0.34459361 0.47881563]
IC 95% θ3: [0.24327018 0.36566246]
Inoltre vediamo che gli intervalli di confidenza al 95%, relativi ai rispettivi errori standard, contengono il vero valore del parametro e quindi possiamo concludere che abbiamo un buon adattamento con il nostro modello MA(3), come ci si dovrebbe aspettare.
Conclusioni
Abbiamo esaminato in dettaglio il modello a media mobile (MA) di ordine q e abbiamo verificato che sono in grado di spiegare parte dell’autocorrelazione. Come già visto per il modello autogressivo dell’ordine p. Entrambi i modelli non riescono a modellare il clustering di volatilità e gli effetti a memoria lunga.
È finalmente giunto il momento di rivolgere la nostra attenzione alla combinazione di questi due modelli, ovvero la Media Mobile Autoregressiva di ordine p e q, ARMA(p,q) per vedere se migliorerà ulteriormente la situazione.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

