In questa lezione descriviamo il modello autoregressivo a media mobile (ARMA) di ordine p,q. Nelle precedenti lezioni abbiamo introdotto i modelli autoregressivi e i modelli a media mobile. Ora combiniamo entrambi per ottenere un modello più sofisticato.
In definitiva, arriviamo ai modelli ARIMA e GARCH che ci aiutano a prevedere i rendimenti degli asset e a stimare la volatilità. Usiamo questi modelli come base per costruire segnali di trading e strategie di gestione del rischio.
Applichiamo il seguente schema per analizzare un modello di serie temporali:
- Motivazione – Spieghiamo perché ci interessa questo particolare modello.
- Definizione – Forniamo una definizione matematica per evitare ambiguità.
- Correlogramma – Disegniamo un correlogramma di esempio per osservare il comportamento del modello.
- Simulazione e adattamento – Adattiamo il modello alle simulazioni per comprenderlo a fondo.
- Dati finanziari reali – Applichiamo il modello ai dati storici reali degli asset.
- Predizione – Prevediamo i valori futuri per generare segnali o filtri di trading.
Criterio di informazione bayesiano
Nelle lezioni precedenti abbiamo descritto il Criterio di Informazione di Akaike (AIC) come strumento per scegliere tra i migliori modelli di serie temporali.
Utilizziamo anche il Bayesian Information Criterion (BIC), uno strumento strettamente correlato. Il BIC si comporta in modo simile all’AIC, poiché penalizza i modelli con troppi parametri, riducendo così il rischio di sovra-adattamento. Tuttavia, il BIC applica una penalizzazione più rigorosa ai parametri aggiuntivi.
Criterio di informazione bayesiano
Consideriamo la funzione di verosimiglianza per un modello statistico con K parametri e L che massimizza la verosimiglianza. Allora, il criterio di informazione bayesiano si calcola come:
\(\begin{eqnarray}BIC = -2 \text{log} (L) + k \text{log}(n)\end{eqnarray}\)
Dove \(n\) rappresenta il numero di punti dati nella serie temporale.
Utilizziamo AIC e BIC per selezionare i modelli ARMA(p,q) più adatti all’analisi delle serie storiche finanziarie.
Test Ljung-Box
Il test di Ljung-Box rappresenta un test di ipotesi fondamentale per verificare se un gruppo di autocorrelazioni associate a un modello di serie temporali differisce significativamente da zero. Il test non analizza la casualità di ogni singolo ritardo, ma valuta l’insieme dei ritardi.
Formalmente:
Test Ljung-Box
Definiamo l’ipotesi nulla \({\bf H_0}\) come: i dati delle serie temporali a ogni ritardo risultano iid, ovvero senza correlazioni seriali nella popolazione.
Definiamo l’ipotesi alternativa \({\bf H_a}\) come: i dati delle serie temporali non risultano iid e mostrano correlazione seriale.
Calcoliamo il seguente test statistico, \(Q\):
\(\begin{eqnarray}Q = n (n+2) \sum_{k=1}^{h} \frac{\hat{\rho}^2_k}{n-k}\end{eqnarray}\)
Dove n rappresenta la lunghezza del campione, \(\hat{\rho}_k\) l’autocorrelazione campionaria al ritardo k e h il numero di ritardi considerati.
Applichiamo la regola: rifiutiamo l’ipotesi nulla \({\bf H_0}\) se \(Q > \chi^2_{\alpha,h}\), con riferimento alla distribuzione chi quadrato con h gradi di libertà al percentile \(100(1-\alpha)\).
Nonostante i calcoli del test appaiano complessi, sfruttiamo Python per eseguire il test, rendendo la procedura più accessibile.
Modello autoregressivo a media mobile (ARMA) di ordine p, q
Ora che abbiamo analizzato il BIC e il test Ljung-Box, possiamo descrivere il nostro primo modello misto: il modello autoregressivo a media mobile (ARMA) di ordine p, q.
Fondamento logico
Fino ad ora abbiamo esplorato i processi autoregressivi e quelli a media mobile.
Nel primo caso, utilizziamo il comportamento passato della serie come input per catturare gli effetti dei partecipanti al mercato, come il momentum e il mean-reverting nel trading azionario.
Nel secondo, impieghiamo il modello per descrivere le informazioni di tipo “shock” presenti nella serie, come un annuncio di utili a sorpresa o un evento inatteso (ad esempio, la fuoriuscita di petrolio della BP Deepwater Horizon).
Un modello ARMA consente di includere entrambi gli aspetti durante la modellazione delle serie temporali finanziarie.
Dobbiamo ricordare che il modello autoregressivo a media mobile (ARMA) non rappresenta il clustering della volatilità, un fenomeno empirico chiave nelle serie finanziarie. Non consideriamo l’eteroscedasticità condizionata. Per modellarla, ci affideremo ai modelli ARCH e GARCH.
Definizione
Costruiamo il modello ARMA(p,q) come combinazione lineare di due modelli lineari; di conseguenza, anche esso risulta lineare:
Modello autoregressivo a media mobile (ARMA) di ordine p, q
Definiamo un modello per la serie storica \(\{ x_t \}\) come ARMA(p,q) se:
\(\begin{eqnarray}x_t = \alpha_1 x_{t-1} + \alpha_2 x_{t-2} + \ldots + w_t + \beta_1 w_{t-1} + \beta_2 w_{t-2} \ldots + \beta_q w_{t-q}\end{eqnarray}\)
Qui \(\{ w_t \}\) rappresenta il rumore bianco con \(E(w_t) = 0\) e varianza \(\sigma^2\).
Utilizziamo l’operatore di ritardo B e riscriviamo l’equazione come funzione di \(\theta\) e \(\phi\) in B:
\(\begin{eqnarray}\theta_p ({\bf B}) x_t = \phi_q ({\bf B}) w_t\end{eqnarray}\)
Quando impostiamo \(p \neq 0\) e \(q=0\), otteniamo il modello AR(p). Se invece poniamo \(p=0\) e \(q \neq 0\), otteniamo il modello MA(q).
Le caratteristiche principali del modello ARMA includono moderazione e ridondanza nei parametri. Infatti, spesso possiamo usare meno parametri rispetto ai modelli AR(p) o MA(q) separatamente. Inoltre, se riscriviamo l’equazione usando BSO, i polinomi \(\theta\) e \(\phi\) possono condividere un fattore comune, semplificando così il modello.
Simulazioni e Correlogrammi
Come abbiamo fatto per i modelli autoregressivi e a media mobile, ora simuliamo diverse serie ARMA e applichiamo i relativi modelli a queste realizzazioni. In questo modo esploriamo la procedura di adattamento, includendo il calcolo degli intervalli di confidenza e verificando se la procedura riesce a stimare correttamente i parametri ARMA originari.
Nella parte 1 e nella parte 2, abbiamo generato manualmente le serie AR e MA estraendo \(N\) campioni da una distribuzione normale e costruito i modelli applicando i ritardi a tali campioni.
ARMA(1,1)
Partiamo dal modello autoregressivo a media mobile (ARMA) più semplice non banale: il modello ARMA(1,1). In questo caso combiniamo un modello autoregressivo di ordine uno con un modello a media mobile di ordine uno. Il modello presenta solo due coefficienti, \(\alpha\) e \(\beta\), che rappresentano rispettivamente il primo ritardo della serie storica e il termine “shock” derivante dal rumore bianco. La forma del modello è:
\(\begin{eqnarray}x_t = \alpha x_{t-1} + w_t + \beta w_{t-1}\end{eqnarray}\)
Prima di avviare la simulazione, definiamo i coefficienti. Impostiamo \(\alpha = 0.5\) e \(\beta = 0.5\).
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.arima_process import ArmaProcess
# Imposta il seed per la riproducibilità
np.random.seed(1)
# Definizione dei parametri ARMA(1,1)
phi = 0.5 # coefficiente AR
theta = -0.5 # coefficiente MA
# Definizione del modello (attenzione al segno)
ar = np.array([1, -phi]) # coefficiente AR in forma caratteristica
ma = np.array([1, theta]) # coefficiente MA
# Simulazione
np.random.seed(1)
arma_process = ArmaProcess(ar, ma)
x = arma_process.generate_sample(nsample=1000)
# Plot della serie simulata
plt.plot(x)
plot_acf(x, lags=30)
plt.show()
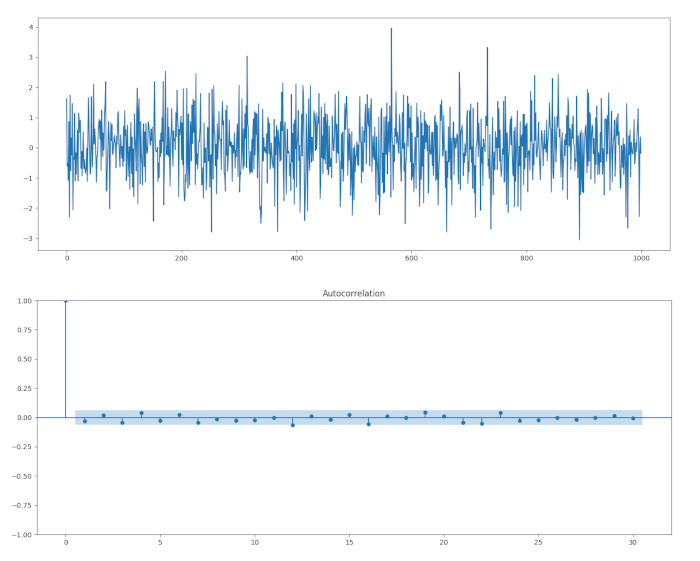
Dal correlogramma possiamo vedere che non c’è un’autocorrelazione significativa, come prevedibile da un modello ARMA(1,1).
Infine, proviamo a determinare i coefficienti e i loro errori standard utilizzando la funzione ARIMA della libreria Statsmodels:
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(x, order=(1, 0, 1))
result = model.fit()
print(result.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARIMA(1, 0, 1) Log Likelihood -1397.793
Date: AIC 2803.586
Time: 10:17:02 BIC 2823.217
Sample: 0 HQIC 2811.048
- 1000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0387 0.030 1.274 0.203 -0.021 0.098
ar.L1 -0.7935 0.202 -3.934 0.000 -1.189 -0.398
ma.L1 0.7551 0.218 3.459 0.001 0.327 1.183
sigma2 0.9585 0.041 23.657 0.000 0.879 1.038
===================================================================================
Ljung-Box (L1) (Q): 0.16 Jarque-Bera (JB): 3.61
Prob(Q): 0.69 Prob(JB): 0.16
Heteroskedasticity (H): 1.00 Skew: -0.08
Prob(H) (two-sided): 0.96 Kurtosis: 3.25
===================================================================================
Possiamo calcolare gli intervalli di confidenza al 95% per ciascun parametro utilizzando gli errori standard:
ar1 = result.params[1]
ma1 = result.params[2]
se_ar1 = result.bse[1]
se_ma1 = result.bse[2]
# Intervalli di confidenza 95%
ci_ar1 = ar1 + np.array([-1.96, 1.96]) * se_ar1
ci_ma1 = ma1 + np.array([-1.96, 1.96]) * se_ma1
print("IC 95% AR(1):", ci_ar1)
print("IC 95% MA(1):", ci_ma1)
IC 95% AR(1): [-1.18888368 -0.39813188]
IC 95% MA(1): [0.32724963 1.18288939]
Gli intervalli di confidenza contengono i valori veri dei parametri in entrambi i casi, ma è importante notare che sono piuttosto ampi, a causa degli errori standard relativamente grandi.
ARMA(2,2)
Proviamo ora un modello ARMA(2,2). Ovvero, un modello AR(2) combinato con un modello MA(2). Dobbiamo specificare quattro parametri per questo modello \(\alpha_1\), \(\alpha_2\), \(\beta_1\), \(\beta_2\).
Consideriamo \(\alpha_1 = 0.5\), \(\alpha_1 = -0.25\), \(\beta_1 = 0.5\) e \(\beta_2 = -0.3\):
import matplotlib.pyplot as plt
import numpy as np
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.graphics.tsaplots import plot_acf
ar1 = np.array([1, -0.5, 0.25])
ma1 = np.array([1, 0.5, -0.3])
simulated_ARMA_data = ArmaProcess(ar1, ma1).generate_sample(nsample=1000)
plt.plot(simulated_ARMA_data)
plot_acf(simulated_ARMA_data, alpha=1, lags=30)
plt.show()
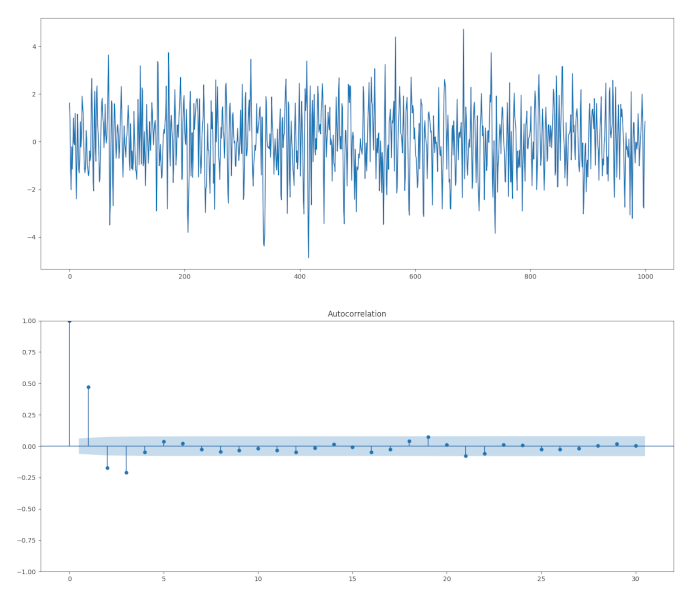
from statsmodels.tsa.arima.model import ARIMA
# Stima del modello ARMA(2,2)
model = ARIMA(x, order=(2, 0, 2))
results = model.fit()
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARIMA(2, 0, 2) Log Likelihood -1395.703
Date: AIC 2803.407
Time: 12:21:43 BIC 2832.853
Sample: 0 HQIC 2814.598
- 1000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0625 0.048 1.292 0.196 -0.032 0.157
ar.L1 0.4891 0.122 4.017 0.000 0.250 0.728
ar.L2 -0.2702 0.033 -8.190 0.000 -0.335 -0.206
ma.L1 0.4905 0.126 3.877 0.000 0.243 0.738
ma.L2 -0.2717 0.116 -2.350 0.019 -0.498 -0.045
sigma2 0.9530 0.041 23.403 0.000 0.873 1.033
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 4.01
Prob(Q): 0.98 Prob(JB): 0.13
Heteroskedasticity (H): 1.02 Skew: -0.07
Prob(H) (two-sided): 0.83 Kurtosis: 3.27
===================================================================================
ar1 = result.params[1]
ar2 = result.params[2]
ma1 = result.params[3]
ma2 = result.params[4]
se_ar1 = result.bse[1]
se_ar2 = result.bse[2]
se_ma1 = result.bse[3]
se_ma2 = result.bse[4]
# Intervalli di confidenza 95%
ci_ar1 = ar1 + np.array([-1.96, 1.96]) * se_ar1
ci_ar2 = ar2 + np.array([-1.96, 1.96]) * se_ar2
ci_ma1 = ma1 + np.array([-1.96, 1.96]) * se_ma1
ci_ma2 = ma2 + np.array([-1.96, 1.96]) * se_ma2
print("IC 95% AR(1):", ci_ar1)
print("IC 95% AR(2):", ci_ar2)
print("IC 95% MA(1):", ci_ma1)
print("IC 95% MA(2):", ci_ma2)
IC 95% AR(1): [0.25041264 0.72771175]
IC 95% AR(2): [-0.33481549 -0.20550619]
IC 95% MA(1): [0.24252497 0.73838166]
IC 95% MA(2): [-0.49834463 -0.04504921]
Tuttavia, per fare trading, ci basta disporre di un potere predittivo che superi la casualità (come il lancio di una moneta) e ci garantisca un profitto sufficiente, al netto dei costi di transazione, per risultare redditizi nel lungo periodo.
Ora che abbiamo esplorato alcuni esempi di modelli ARMA simulati, dobbiamo definire un metodo che ci consenta di scegliere i valori di p e q quando adattiamo i modelli ai dati finanziari reali.
Scegliere il miglior modello ARMA(p,q)
Per stabilire quale ordine \(p,q\) del modello autoregressivo a media mobile (ARMA) risulti adeguato per una serie, utilizziamo l’AIC (oppure il BIC) su un sottoinsieme di valori per \(p,q\) e applichiamo il test di Ljung-Box per verificare se otteniamo un buon adattamento con specifici valori di \(p,q\).
Per spiegare questo approccio, simuliamo prima un particolare processo ARMA(p,q). Poi eseguiamo un ciclo su tutte le coppie \(p \in \{ 0,1,2,3,4 \}\) e \(q \in \{ 0,1,2,3,4 \}\), calcolando l’AIC per ciascuna. Scegliamo il modello con l’AIC più basso ed eseguiamo il test di Ljung-Box sui residui per confermare se abbiamo ottenuto un buon adattamento.
Iniziamo simulando una serie ARMA(3,2):
import numpy as np
import statsmodels.api as sm
import itertools
import matplotlib.pyplot as plt
np.random.seed(2)
# Simuliamo un processo ARMA(3,2) con coefficienti specificati
arparams = np.array([0.5, -0.25, 0.4])
maparams = np.array([0.5, -0.3])
ar = np.r_[1, -arparams] # statsmodels usa coefficenti negativi per AR
ma = np.r_[1, maparams]
x = sm.tsa.arma_generate_sample(ar, ma, nsample=1000)
Ora esaminiamo diversi valori di p e q e scegliamo i valori che puntano a AIC e/o BIC più piccoli.
Creiamo ora un oggetto best_model per memorizzare il miglior modello adattato e il valore più basso dell’AIC. Eseguiamo un ciclo su tutte le combinazioni possibili di p e q, utilizzando un oggetto temporaneo per salvare l’adattamento del modello ARMA(i,j), dove i e j sono le variabili del ciclo.
Se l’AIC corrente risulta inferiore a qualsiasi AIC calcolato in precedenza, aggiorniamo il valore finale dell’AIC con quello corrente e selezioniamo quell’ordine. Al termine del ciclo, l’ordine del modello ARMA sarà memorizzato in best_order, mentre l’adattamento ARIMA(p,d,q) (con il componente “Integrato” d impostato a 0) sarà memorizzato in best_model.
Formalmente, stiamo cercando di minimizzare l’AIC tra i modelli ARMA(p,q), ovvero:
\( \text{AIC} = -2 \log L + 2k \)
dove \( L \) è la verosimiglianza massima del modello e \( k \) è il numero di parametri stimati.
# Ora cerchiamo l'ordine ottimale (p, q) per un modello ARMA utilizzando il criterio AIC
best_aic = np.inf
best_order = None
best_model = None
# Proviamo tutte le combinazioni (p, q) con p e q da 0 a 4
for p, q in itertools.product(range(5), range(5)):
try:
model = sm.tsa.ARIMA(x, order=(p, 0, q)).fit()
current_aic = model.aic
if current_aic < best_aic:
best_aic = current_aic
best_order = (p, 0, q)
best_model = model
except:
continue
# Stampiamo i risultati finali
print("AIC finale:", best_aic)
print("Ordine ARMA trovato:", best_order)
print(best_model.summary())
Dopo aver eseguito il fitting dei modelli su diversi ordini p e q, possiamo valutare i risultati e ricavare l’ordine del modello migliore in base all’AIC minore.
AIC finale: 2856.0201478738413
Ordine ARMA trovato: (3, 0, 2)
Possiamo vedere che è l’ordine originale del modello ARMA simulato è stato selezionato come ordine migliore, cioè \(p=3\) e \(q=2\).
A conferma della bontà della nostra selezione, possiamo stampare il report prodotto dalla funzione ARMA dove si evidenzia che parametri stimati sono molto vicini ai valore reali. Inoltre l’intervallo di confidenza al 95% contiene i valori dei parametri veri e quindi possiamo giudicare il modello adatto.
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARIMA(3, 0, 2) Log Likelihood -1421.010
Date: AIC 2856.020
Time: 12:52:23 BIC 2890.374
Sample: 0 HQIC 2869.077
- 1000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.1667 0.101 -1.644 0.100 -0.365 0.032
ar.L1 0.5543 0.075 7.353 0.000 0.407 0.702
ar.L2 -0.2566 0.040 -6.438 0.000 -0.335 -0.179
ar.L3 0.3659 0.034 10.904 0.000 0.300 0.432
ma.L1 0.4216 0.077 5.498 0.000 0.271 0.572
ma.L2 -0.3547 0.073 -4.861 0.000 -0.498 -0.212
sigma2 1.0018 0.043 23.319 0.000 0.918 1.086
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 7.27
Prob(Q): 0.95 Prob(JB): 0.03
Heteroskedasticity (H): 0.83 Skew: 0.18
Prob(H) (two-sided): 0.09 Kurtosis: 3.22
===================================================================================
from statsmodels.graphics.tsaplots import plot_acf
# Get residuals of the model
resid = res.resid
# Plot ACF of residuals
plot_acf(resid, alpha=1, lags=30)
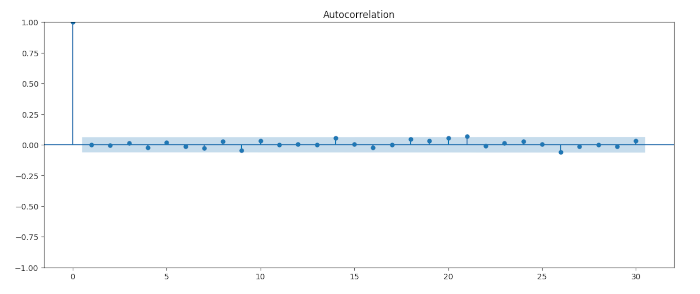
from statsmodels.stats.diagnostic import acorr_ljungbox
# Ljung-Box test
resid = best_model.resid
ljung_box_result = acorr_ljungbox(resid, lags=[20], return_df=True)
print(ljung_box_result)
lb_stat lb_pvalue
15.390138 0.753666
Analisi del modello per l’indice S&P500
Ora che abbiamo delineato la procedura per scegliere il modello di serie temporale ottimale per una serie simulata, è piuttosto semplice applicarlo ai dati finanziari. Per questo esempio scegliamo l’indice S&P500 dell’azionariato statunitenze. Scarichiamo i prezzi di chiusura giornalieri utilizzando yfinance e quindi creiamo il flusso dei ritorni logaritmici:
import numpy as np
import pandas as pd
import yfinance as yf
data = yf.download("^GSPC", period="max")
sp500 = np.log(data['Adj Close'] / data['Adj Close'].shift(1)).dropna()
import statsmodels.api as sm
import itertools
# Ricerca del modello ARMA(p,q) ottimale (con d=0) usando l'AIC
best_aic = np.inf
best_order = None
best_model = None
# Proviamo tutte le combinazioni (p, q) con p e q da 0 a 4
for p, q in itertools.product(range(5), range(5)):
for q in range(5):
try:
model = sm.tsa.ARIMA(log_returns, order=(p, 0, q)).fit()
current_aic = model.aic
if current_aic < best_aic:
best_aic = current_aic
best_order = (p, 0, q)
best_model = model
except:
continue
print("Ordine migliore:", best_order)
p = 4
q = 3
# Plot dell'ACF dei residui del modello ottimale
residuals = best_model.resid
sm.graphics.tsa.plot_acf(residuals.dropna(), lags=30)
plt.show()
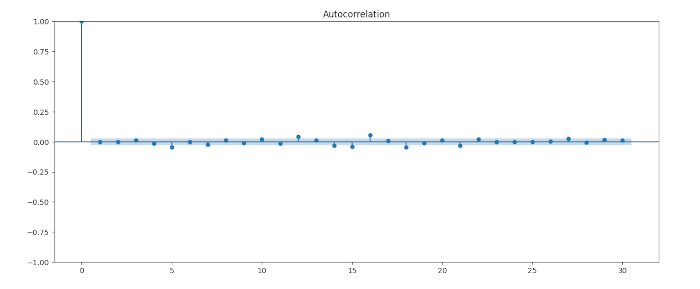
from statsmodels.stats.diagnostic import acorr_ljungbox
# Ljung-Box test
resid = best_model.resid
ljung_box_result = acorr_ljungbox(resid, lags=[20], return_df=True)
print(ljung_box_result)
Ljung-Box test: 40.390954304955045
p-value: 0.0044565024322041746
Come avevamo previsto, il p-value risulta inferiore a 0,05, quindi non possiamo affermare che i residui rappresentino una realizzazione di rumore bianco discreto. Di conseguenza, rileviamo ancora autocorrelazione nei residui, non spiegata dal modello ARMA(4,3) che abbiamo adattato.
Conclusioni
Durante l’analisi delle serie temporali con il modello autoregressivo a media mobile (ARMA), abbiamo identificato segni evidenti di eteroschedasticità condizionale (cluster di volatilità) nella serie S&P500, soprattutto nei periodi intorno al 2007-2008. Nelle prossime lezioni, quando introdurremo il modello GARCH, impareremo a rimuovere queste autocorrelazioni residui.
In generale, riteniamo che i modelli ARMA non offrano un’adeguata rappresentazione dei rendimenti logaritmici azionari. Per questo motivo, teniamo conto dell’eteroschedasticità condizionale e combiniamo i modelli ARIMA e GARCH. Nella prossima lezione descriveremo il modello ARIMA e chiariremo come il componente “Integrato” si differenzi dal modello ARMA che abbiamo studiato in questa lezione.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

