Nelle prossime lezioni descriviamo il modello autoregressivo AR di ordine p, che insieme al modello a media mobile (MA) di ordine q e il modello autoregressivo a media mobile (ARMA) di ordine misto (p, q). Questi modelli ci permettono di catturare o “spiegare” la correlazione seriale all’interno di uno strumento e ci offrono un mezzo utile per le previsioni dei prezzi futuri.
Nell’ultima lezione abbiamo analizzato il White Noise e Random Walk come modelli di base per le serie temporali di strumenti finanziari. Abbiamo osservato che in certi casi il modello di Random Walk non riesce a cogliere appieno il comportamento di autocorrelazione dello strumento. Per questo motivo utilizziamo modelli più sofisticati.
Sappiamo però che le serie temporali finanziarie presentano una caratteristica chiamata clustering di volatilità: la volatilità dello strumento varia nel tempo. Questo comportamento, che definiamo eteroschedasticità condizionale, non viene gestito dai modelli AR, MA e ARMA, poiché non considerano questa dinamica. Per produrre previsioni accurate, dobbiamo quindi adottare un modello più avanzato.
Tra questi modelli troviamo il modello Autoregressivo a Varianza Condizionata (ARCH) e il modello Generalizzato ARCH (GARCH), oltre a molte varianti. Il modello GARCH ricopre un ruolo centrale nella finanza quantitativa e lo utilizziamo spesso per simulare serie temporali finanziarie e stimare il rischio.
Introduzione
Come in tutte le lezioni di TradingQuant, costruiamo i modelli partendo dalle versioni più semplici per comprendere come ogni variante influenzi la nostra capacità predittiva. Anche se il modello autoregressivo (AR) di ordine p, e gli altri modelli MA e ARMA risultano relativamente semplici, costituiscono le fondamenta di modelli più complessi come l’Autoregressive Integrated Moving Average (ARIMA) e della famiglia GARCH. Per questo motivo li studiamo in dettaglio.
Una delle nostre prime strategie di trading nella serie di lezioni dedicate alle serie temporali prevede la combinazione di ARIMA e GARCH per prevedere i prezzi con n-periodi di anticipo. Prima di applicare questa combinazione a una strategia reale, esploreremo in dettaglio sia ARIMA che GARCH.
In questa lezione introduciamo alcuni concetti fondamentali delle serie temporali che ritroveremo nei modelli successivi, in particolare la stazionarietà rigorosa e il criterio dell’informazione di Akaike (AIC).
Studio dei modelli
Dopo averli introdotti, seguiamo lo schema tradizionale che adottiamo nello studio dei modelli di serie temporali:
- Razionale – Spieghiamo perché ci interessa uno specifico modello. Quali effetti riesce a catturare? Cosa otteniamo (o perdiamo) aggiungendo complessità?
- Definizione – Forniamo la definizione matematica completa e la relativa notazione per evitare ambiguità.
- Proprietà del secondo ordine – Analizziamo, e a volte deriviamo, le proprietà di secondo ordine del modello: media, varianza e funzione di autocorrelazione.
- Correlogramma – Tracciamo il correlogramma di una realizzazione del modello sfruttando le proprietà di secondo ordine per visualizzarne il comportamento.
- Simulazione – Simuliamo le realizzazioni del modello e lo adattiamo a tali simulazioni per assicurarci che l’implementazione sia accurata e comprensibile.
- Dati finanziari reali – Adattiamo il modello a dati finanziari reali e analizziamo il correlogramma dei residui per valutare se il modello gestisce correttamente la correlazione seriale della serie originale.
- Pronostico – Eseguiamo n-step ahead forecasts per specifiche realizzazioni del modello, al fine di generare segnali di trading.
Quasi tutte le lezioni che dedichiamo ai modelli di serie temporali seguono questo schema, così possiamo confrontare facilmente le differenze tra i vari modelli man mano che introduciamo nuova complessità.
Cominciamo ora con lo studio della stazionarietà rigorosa e del criterio AIC.
Stazionarietà Rigorosa
Abbiamo già definito la stazionarietà nella lezione sulla correlazione seriale. Ora, poiché analizziamo molte serie finanziarie con frequenze diverse, ci assicuriamo che i modelli tengano conto della volatilità che cambia nel tempo. In particolare, consideriamo la loro eteroschedasticità.
Affrontiamo questo problema quando adattiamo specifici modelli alle serie storiche. In generale, non possiamo ignorare la correlazione seriale nei residui se non teniamo conto dell’eteroschedasticità. Questo ci riporta al concetto di stazionarietà. Per definizione, una serie presenta varianza non stazionaria se la sua volatilità cambia nel tempo.
Per questo motivo introduciamo una definizione più rigorosa: la stazionarietà rigorosa.
Serie rigorosamente stazionaria Definiamo una serie storica, \(\{ x_t \}\), rigorosamente stazionaria se la distribuzione congiunta degli elementi \(x_{t_1},\ldots,x_{t_n}\) coincide con quella di \(x_{t_{1}+m},\ldots,x_{t_{n}+m}\), per ogni valore di m.
Possiamo interpretare questa definizione dicendo che la distribuzione della serie temporale resta invariata per qualsiasi spostamento arbitrario nel tempo. In particolare, una serie rigorosamente stazionaria mantiene costanti nel tempo la media, la varianza e l’autocovarianza tra \(x_t\) e \(x_s\), che dipende soltanto da \(|t-s|\).
Riprenderemo l’argomento delle serie rigorosamente stazionarie nelle prossime lezioni.
Criterio di informazione di Akaike (AIC)
Nelle lezioni precedenti abbiamo anticipato la necessità di confrontare diversi modelli per scegliere il “migliore”. Questo approccio vale sia per l’analisi delle serie temporali, sia per il machine learning e più in generale per la statistica.
Al momento adottiamo due criteri principali: l’Akaike Information Criterion (AIC) e il Bayesian Information Criterion, che descritto nel corso sulla statistica bayesiana.
Introduciamo brevemente l’AIC, che utilizziamo nella nelle prossime lezioni.
L’AIC rappresenta uno strumento utile per selezionare i modelli. Quando disponiamo di una serie di modelli statistici, comprese le serie temporali, l’AIC ci permette di stimare la “qualità” di ciascun modello rispetto agli altri disponibili.
Basandoci sulla teoria dell’informazione, un argomento affascinante e complesso, bilanciamo la complessità del modello (ovvero il numero di parametri) con la sua capacità di adattarsi ai dati. Ecco la definizione:
Criterio informativo di Akaike Supponiamo di utilizzare la funzione di verosimiglianza per un modello statistico con \(k\) parametri, e che \(L\) rappresenti il valore che massimizza la verosimiglianza. Allora il criterio informativo di Akaike si esprime come: \(\begin{eqnarray}AIC = -2 \text{log} (L) + 2k \end{eqnarray}\)
Scegliamo come “migliore” il modello che presenta l’AIC più basso tra tutti. Notiamo che l’AIC cresce con il numero di parametri k, ma diminuisce quando la log-verosimiglianza negativa aumenta. In sostanza, penalizziamo i modelli che fanno overfitting.
Nel seguito, descriviamo i modelli AR, MA e ARMA con ordini diversi. Nella prossima lezione presentiamo un metodo basato sull’AIC per selezionare il miglior modello ARMA in base a un determinato set di dati.
Modello autoregressivo (AR) di ordine p
Il primo modello che analizziamo, base di questa lezione, è il modello autoregressivo (AR) di ordine p, comunemente abbreviato in AR(p).
Definizione
Nella lezione precedente abbiamo descritto il random walk, dove ogni termine \(x_t\) dipende unicamente dal termine precedente \(x_{t-1}\) e da un termine stocastico di rumore bianco \(w_t\):
\(\begin{eqnarray} x_t = x_{t-1} + w_t \end{eqnarray}\)
Abbiamo esteso il modello di passeggiata casuale includendo termini più arretrati nel tempo. La struttura del modello rimane lineare, cioè dipende linearmente dai valori passati con relativi coefficienti. Da qui nasce il termine “regressivo” in “autoregressivo”: si tratta, infatti, di una regressione in cui utilizziamo i termini precedenti come predittori.
Modello autoregressivo (AR) di ordine p
Un modello di serie storica, \(\{ x_t \}\), è un modello autoregressivo di ordine p, AR(p), se:\(\begin{eqnarray}
x_t &=& \alpha_1 x_{t-1} + \ldots + \alpha_p x_{t-p} + w_t \\
&=& \sum_{i=1}^p \alpha_i x_{t-i} + w_t
\end{eqnarray}\)Dove \(\{ w_t \}\) rappresenta il rumore bianco e \(\alpha_i \in \mathbb{R}\), con \(\alpha_p \neq 0\) per definire un processo AR di ordine p.
Se applichiamo l’operatore di spostamento all’indietro, B (vedi lezione precedente), riscriviamo il modello come funzione θ di B:
\(\begin{eqnarray}
\theta_p ({\bf B}) x_t = (1 – \alpha_1 {\bf B} – \alpha_2 {\bf B}^2 – \ldots – \alpha_p {\bf B}) x_t = w_t
\end{eqnarray}\)
Notiamo subito che una passeggiata casuale corrisponde a un AR(1) con \(\alpha_1\) uguale a uno. Come anticipato, il modello autoregressivo rappresenta un’estensione naturale del random walk: tutto torna!
Applicazione
Prevediamo facilmente con il modello AR(p): una volta stimati i coefficienti \(\alpha_i\), otteniamo la previsione:
\(\begin{eqnarray}
\hat{x}_t = \alpha_1 x_{t-1} + \ldots + \alpha_p x_{t-p}
\end{eqnarray}\)
Possiamo poi estendere le previsioni a n-passi avanti, producendo \(\hat{x}_t\), \(\hat{x}_{t+1}\), \(\hat{x}_{t+2}\) e così via fino a \(\hat{x}_{t+n}\). Nelle prossime lezioni descriveremo i modelli ARMA e utilizzeremo una funzione Python per generare previsioni, insieme alle bande di confidenza, utili per produrre segnali di trading.
Stazionarietà per processi autoregressivi
Tra gli aspetti più critici del modello AR(p) troviamo la stazionarietà, che non sempre risulta garantita. La dipendenza dalla stazionarietà deriva dai parametri del modello.
Per capire se un processo AR(p) è stazionario, risolviamo la sua equazione caratteristica, che otteniamo riscrivendo il modello autoregressivo (AR) di ordine p in forma di spostamento all’indietro, impostandolo a zero:
\(\begin{eqnarray}
\theta_p({\bf B}) = 0
\end{eqnarray}\)
Risolvendo per B, otteniamo le radici dell’equazione. Per garantire la stazionarietà del processo, dobbiamo verificare che i valori assoluti di tutte le radici siano maggiori di uno. Questa condizione si rivela utile per testare rapidamente la stazionarietà del processo AR(p).
Osserviamo ora alcuni esempi per chiarire meglio il concetto:
- Random Walk – Nel processo AR(1) con \(\alpha_1 = 1\) otteniamo l’equazione \(\theta = 1 – {\bf B}\). La radice \({\bf B} = 1\) ci indica che la serie non è stazionaria.
- AR(1) – Scegliendo \(\alpha_1 = \frac{1}{4}\), otteniamo \(x_t = \frac{1}{4} x_{t-1} + w_t\), con equazione caratteristica \(1 – \frac{1}{4} {\bf B} = 0\), che ha radice \({\bf B} = 4 > 1\): dunque, il processo è stazionario.
- AR(2) – Impostando \(\alpha_1 = \alpha_2 = \frac{1}{2}\), otteniamo \(x_t = \frac{1}{2} x_{t-1} + \frac{1}{2} x_{t-2} + w_t\), con equazione \(-\frac{1}{2}({\bf B-1})({\bf B+2}) = 0\). Le radici risultano \({\bf B} = 1, -2\). La presenza della radice unitaria indica una serie non stazionaria. Tuttavia, altri processi AR(2) risultano stazionari.
Proprietà del secondo ordine
La media di un processo AR(p) è pari a zero. Le autocovarianze e autocorrelazioni seguono invece relazioni ricorsive, chiamate equazioni di Yule-Walker. Ecco le proprietà fondamentali:
\(\begin{eqnarray}
\mu_x = E(x_t) = 0
\end{eqnarray}\)\(\begin{eqnarray}
\gamma_k = \sum_{i=1}^p \alpha_i \gamma_{k-i}, \enspace k > 0
\end{eqnarray}\)
\(\begin{eqnarray}
\rho_k = \sum_{i=1}^p \alpha_i \rho_{k-i}, \enspace k > 0
\end{eqnarray}\)
Dobbiamo conoscere i valori dei parametri \(\alpha_i\) per calcolare le autocorrelazioni.
Ora che abbiamo definito le proprietà del secondo ordine, possiamo simulare processi AR(p) di diversi ordini e tracciare i rispettivi correlogrammi.
Simulazioni e Correlogrammi
AR(1)
Iniziamo con un processo AR(1). Questo è simile a una passeggiata casuale, tranne che \(\alpha_1\) non deve eguagliare l’unità. Il nostro modello avrà \(\alpha_1 = 0.6\). Il codice Python per la creazione di questa simulazione è il seguente:
import numpy as np
# Imposta il seed per la riproducibilità
np.random.seed(1)
# Genera 100 rumori bianchi standard
w = np.random.normal(size=100)
# Inizializza la serie AR(1)
simulated_data_1 = np.copy(w)
for t in range(1, 100):
simulated_data_1[t] = 0.6 * simulated_data_1[t - 1] + w[t]
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
# Grafico modello AR
plt.plot(simulated_data_1)
# Grafico Autocorrelazione
plot_acf(simulated_data_1, lags=30)
plt.show()
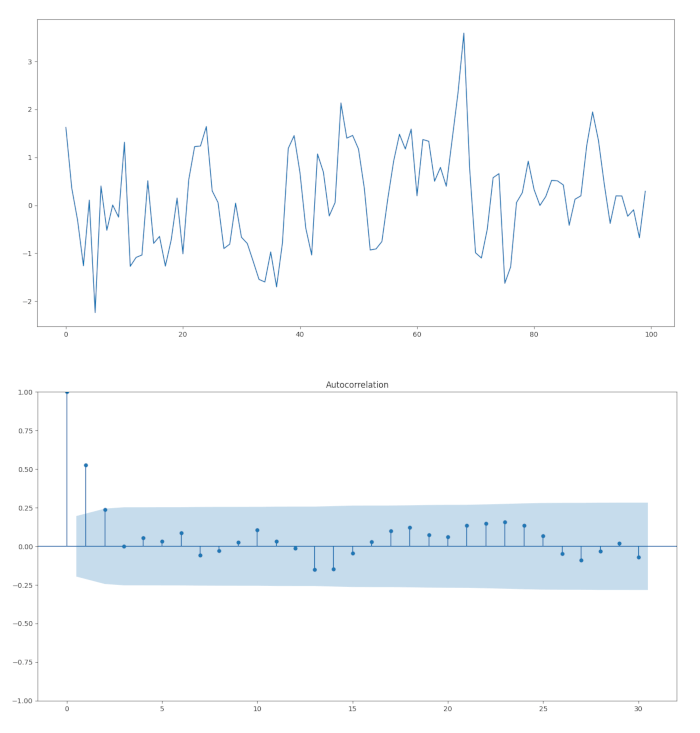
Proviamo ora ad adattare un processo AR(p) ai dati simulati che abbiamo appena generato, per vedere se possiamo recuperare i parametri sottostanti. Abbiamo eseguito una procedura simile nella lezione relativa White Noise e Random Walks.
Python, tramite il pacchetto statsmodels, fornisce una funzione utile chiamata ARIMA per stimare modelli autoregressivi. Possiamo usare questo metodo per determinare innanzitutto il miglior ordine \(\p\) del modello (secondo l’AIC) e ottenere le stime dei parametri per i \(\alpha_i\), che ci permetteranno poi di costruire intervalli di confidenza.
Per completezza, ricreiamo la serie \(\x\) con un processo AR(1):
import numpy as np
np.random.seed(1)
w = np.random.normal(size=100)
x = np.copy(w)
for t in range(1, 100):
x[t] = 0.6 * x[t-1] + w[t]
Usiamo il comando ARIMA per adattare un modello autoregressivo (AR) al nostro processo AR(1) simulato, utilizzando la stima di massima verosimiglianza (MLE) come procedura di adattamento.
Estraiamo innanzitutto l’ordine ottimale del modello:
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(x, order=(1, 0, 0))
result = model.fit()
print(result.model_orders)
{'trend': 0, 'exog': 1, 'ar': 1, 'ma': 0, 'seasonal_ar': 0, 'seasonal_ma': 0, 'reduced_ar': 1, 'reduced_ma': 0, 'exog_variance': 0, 'measurement_variance': 0, 'variance': 1}
La funzione ha identificato correttamente che il modello sottostante è un processo AR(1).
Otteniamo ora la stima del parametro autoregressivo:
phi_hat = result.params[1]
print(phi_hat)
0.530364370958771
La procedura MLE ha prodotto una stima per \(\hat{\alpha_1}\), pari a circa 0.53, leggermente inferiore al valore reale di 0.6.
Infine, possiamo usare l’errore standard (ricavato dalla varianza asintotica) per costruire un intervallo di confidenza al 95% attorno al parametro stimato. Basta moltiplicare il vettore [-1.96, 1.96] per lo standard error:
se = result.bse[1]
conf_int = phi_hat + np.array([-1.96, 1.96]) * se
print(conf_int)
[0.37805711 0.68267163]
Il valore reale del parametro cade all’interno dell’intervallo di confidenza al 95%, come ci aspettiamo, dato che la serie è stata generata proprio da quel modello.
Alpha negativo
Vediamo lo stesso approccio considerando \(\alpha_1 =-0.6\).
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
np.random.seed(1)
w = np.random.normal(size=100)
x = np.copy(w)
for t in range(1, 100):
x[t] = -0.6 * x[t-1] + w[t]
plt.plot(x)
plot_acf(x)
plt.show()
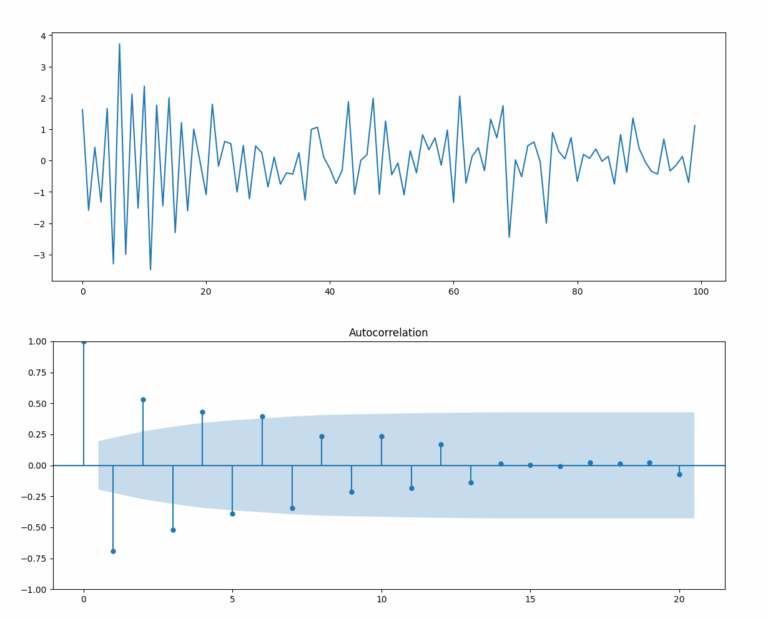
Come fatto in precedenza, possiamo adattare un modello AR(p) con ARIMA:
import numpy as np
from statsmodels.tsa.arima.model import ARIMA
# Riproducibilità
np.random.seed(1)
N = 1000
w = np.random.normal(size=N)
x = np.copy(w)
# Generazione del processo AR(1) con phi = -0.6
for t in range(1, N):
x[t] = -0.6 * x[t - 1] + w[t]
# Modello AR(1) senza intercetta (trend='n' => nessuna costante)
model = ARIMA(x, order=(1, 0, 0), trend='n')
result = model.fit()
# Estrazione dei parametri e intervallo di confidenza
import pandas as pd
params = pd.Series(result.params, index=result.param_names)
bse = pd.Series(result.bse, index=result.param_names)
phi_hat = params['ar.L1']
se = bse['ar.L1']
conf_int = phi_hat + np.array([-1.96, 1.96]) * se
# Output
print("Ordine stimato:", result.model_orders)
print("Stima di phi_1:", phi_hat)
print("Intervallo di confidenza al 95%:", conf_int)
Ordine stimato: {'trend': 0, 'exog': 0, 'ar': 1, 'ma': 0, 'seasonal_ar': 0, 'seasonal_ma': 0, 'reduced_ar': 1, 'reduced_ma': 0, 'exog_variance': 0, 'measurement_variance': 0, 'variance': 1}
Stima di phi_1: -0.6423774581975487
Intervallo di confidenza al 95%: [-0.69012728 -0.59462764]
Ancora una volta abbiamo il corretto ordine del modello, con un’ottima stima \(\hat{\alpha_1}=-0.6423\) del vero valore \(\hat{\alpha_1}=-0.6\). Inoltre, il valore reale cade nuovamente all’interno dell’intervallo di confidenza al 95%.
AR(2)
Aggiungiamo un po’ più di complessità ai nostri processi autoregressivi simulando un modello di ordine 2. In particolare, impostiamo \(\alpha_1=0.666\) e \(\alpha_2 = -0.333\). Ecco il codice completo per simulare e tracciare le realizzazioni, così come il correlogramma per una serie del genere:
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
np.random.seed(1)
N = 100
w = np.random.normal(size=N)
x = w.copy()
for t in range(2, N):
x[t] = 0.666 * x[t-1] - 0.333 * x[t-2] + w[t]
plt.plot(x)
plot_acf(x)
plt.show()
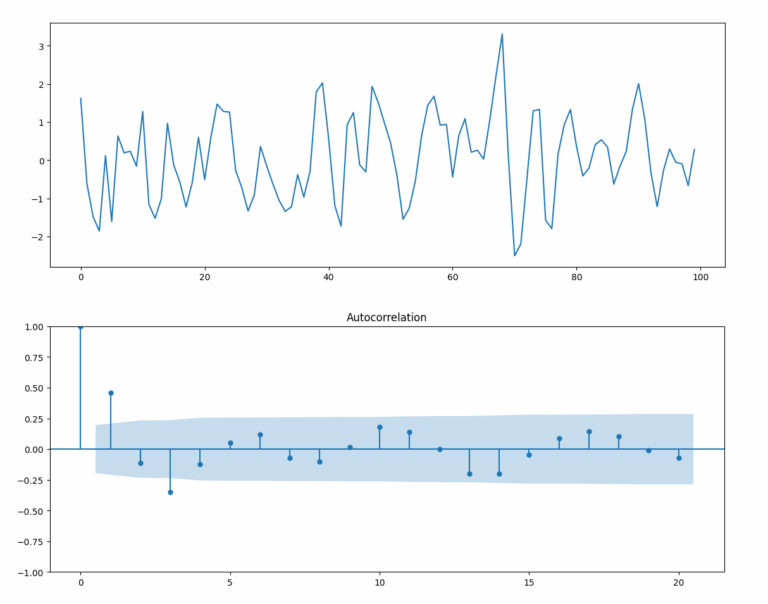
Come prima, notiamo che il correlogramma si discosta in modo significativo da quello di un rumore bianco, come previsto. Si osservano picchi statisticamente significativi.
Anche in questo caso, utilizziamo una funzione per adattare un modello autoregressivo (AR) di ordine p alla nostra realizzazione AR(2). La procedura è simile a quella usata per il modello AR(1):
from statsmodels.tsa.arima.model import ARIMA
np.random.seed(1)
N = 1000
w = np.random.normal(size=N)
x = w.copy()
for t in range(2, N):
x[t] = 0.666 * x[t-1] - 0.333 * x[t-2] + w[t]
model = ARIMA(x, order=(2, 0, 0))
result = model.fit()
print("Ordine stimato:", result.model_orders)
print("Stime dei parametri AR:", result.params[1:3])
Ordine stimato: {'trend': 0, 'exog': 1, 'ar': 2, 'ma': 0, 'seasonal_ar': 0, 'seasonal_ma': 0, 'reduced_ar': 2, 'reduced_ma': 0, 'exog_variance': 0, 'measurement_variance': 0, 'variance': 1}
Stime dei parametri AR: [ 0.64566667 -0.32631026]
L’ordine corretto è stato identificato, e le stime dei parametri \(\hat{\phi}_1 = 0{,}645\) e \(\hat{\phi}_2 = -0{,}326\) non si discostano molto dai valori reali \(\phi_1 = 0{,}666\) e \(\phi_2 = -0{,}333\).
Conclusioni
È interessante osservare che, nel backend, la funzione arima viene utilizzata per stimare il modello AR. Come vedremo nelle prossime lezioni, il modello autoregressivo (AR) di ordine p corrisponde al modello \(\text{ARIMA}(p, 0, 0)\): infatti, un modello AR è un caso particolare di ARIMA senza componenti MA (Media Mobile) né I (Integrazione).
Questo passaggio introduce la serie successiva di modelli, ovvero la media mobile MA(q) e la media mobile autoregressiva ARMA(p, q). Tratteremo entrambi questi approcci nelle prossime lezioni. Come ripetiamo spesso, questi modelli ci condurranno alla famiglia di modelli ARIMA e GARCH, che offrono un adattamento decisamente più efficace alla complessità della correlazione seriale nelle serie temporali dei dati finanziari.
Grazie a questi strumenti, potremo migliorare in modo significativo le nostre previsioni e, in ultima analisi, sviluppare strategie di trading più redditizie.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

