In questa lezione descriviamo il modello autoregressivo generalizzato a eteroschedasticità condizionata di ordine p,q, noto come GARCH(p,q). Utilizziamo ampiamente il modello GARCH nel settore finanziario, poiché molti prezzi delle attività mostrano eteroschedasticità condizionale.
Introduzione
Approfondiamo l’eteroschedasticità condizionale partendo dal modello più semplice, l’ARCH. Successivamente, estendiamo il modello ARCH introducendo il modello GARCH. Infine, applichiamo il GARCH ad alcune serie finanziarie che evidenziano raggruppamenti di volatilità.
Nelle precedenti lezioni abbiamo introdotto i concetti fondamentali e descritto i modelli base fino ad arrivare al modello ARIMA. Nella lezione relativa al modello ARIMA abbiamo effettuato alcune previsioni iniziali. Abbiamo anticipato che possiamo costruire una semplice strategia di trading dopo aver studiato i modelli ARIMA e GARCH. Ora completiamo il quadro esaminando l’eteroschedasticità condizionale e utilizziamola per migliorare la qualità delle nostre previsioni.
Volatilità
Studiamo l’eteroschedasticità condizionata in finanza per analizzare la volatilità dei rendimenti degli asset. La volatilità rappresenta un concetto fondamentale perché si collega strettamente al rischio.
La volatilità trova numerose applicazioni in ambito finanziario:
- Prezzi delle opzioni – Il modello di Black-Scholes per il pricing delle opzioni dipende dalla volatilità dell’asset sottostante
- Risk Management – Usiamo la volatilità per calcolare il VaR di un portafoglio, lo Sharpe Ratio di una strategia e per determinare la leva finanziaria
- Titoli negoziabili – Possiamo ora negoziare la volatilità direttamente attraverso il CBOE Volatility Index (VIX), i relativi future e gli ETF.
Quando riusciamo a prevedere efficacemente la volatilità, possiamo valutare meglio le opzioni, creare strumenti di gestione del rischio più sofisticati per i nostri portafogli di trading algoritmico ed elaborare strategie che negoziano direttamente la volatilità.
Ora ci concentriamo sull’eteroschedasticità condizionata, introducendo definizione e proprietà.
Eteroschedasticità condizionata
Introduciamo il concetto di eteroschedasticità ed esploriamo la componente “condizionale”.
Quando analizziamo un insieme di variabili casuali in un modello di serie temporali, diciamo che l’insieme è eteroschedastico se troviamo gruppi o sottoinsiemi di variabili con varianza diversa rispetto al resto dell’insieme.
Per esempio, in una serie temporale non stazionaria che presenta stagionalità o tendenza, possiamo notare un aumento della varianza legato a queste caratteristiche. Chiamiamo questa variabilità regolare eteroschedasticità.
Nel contesto finanziario, troviamo spesso situazioni in cui un aumento della varianza genera un’ulteriore crescita della varianza.
Pensiamo all’uso dell’assicurazione di protezione del portafoglio da parte dei gestori long-only. Se i mercati registrano una giornata negativa, gli ordini di vendita automatizzati per il controllo del rischio possono abbassare ulteriormente i prezzi delle azioni. Poiché i portafogli più grandi risultano altamente correlati, questa dinamica genera una significativa volatilità al ribasso.
Questi periodi di “svendita”, insieme ad altri fenomeni tipici della volatilità finanziaria, creano un’eteroschedasticità serialmente correlata e quindi condizionata a periodi di elevata varianza. Per questo motivo, parliamo di serie eteroschedastiche condizionate.
Uno degli aspetti più critici delle serie eteroschedastiche condizionate è la difficoltà nel rilevare la volatilità osservando solo il correlogramma. Infatti, quando tracciamo il correlogramma di una serie con elevata volatilità, otteniamo spesso ciò che sembra un rumore bianco stazionario. Tuttavia, la serie in realtà è non stazionaria, poiché la sua varianza varia nel tempo.
In questa lezione descriviamo un metodo per rilevare le serie eteroschedastiche condizionate e applichiamo i modelli ARCH e GARCH per implementarlo, ottenendo previsioni più realistiche e strategie di trading algoritmico più efficaci.
Modello autoregressivo a Eteroschedasticità Condizionata
Abbiamo introdotto l’eteroschedasticità condizionata (CH) e la sua rilevanza nelle serie finanziarie. Ora descriviamo un modello che integra naturalmente la CH. Poiché sappiamo che la classe di modelli ARIMA non considera la CH, come possiamo procedere?
Per affrontare il problema, progettiamo un modello che utilizza un processo autoregressivo applicato alla varianza stessa. In questo modo teniamo conto delle variazioni della varianza nel tempo, sfruttando i valori passati della stessa varianza.
Questa logica costituisce la base del modello Autoregressive Conditional Heteroskedastic (ARCH). Iniziamo con il caso più semplice: un modello ARCH che dipende solo dal valore precedente della varianza nella serie.
Definizione
Modello Autoregressivo a Eteroschedasticità Condizionata di Ordine Unitario
Consideriamo una serie temporale \(\{ \epsilon_t \}\), definita a ogni istante come:\(\begin{eqnarray} \epsilon_t = \sigma_t w_t \end{eqnarray}\)
In cui \(\{ w_t \}\) rappresenta un rumore bianco discreto, con media zero e varianza unitaria, mentre \(\sigma^2_t\) è definita da:
\(\begin{eqnarray} \sigma^2_t = \alpha_0 + \alpha_1 \epsilon^2_{t-1} \end{eqnarray}\)
Qui \(\alpha_0\) e \(\alpha_1\) sono i parametri del modello.
Quindi \(\{ \epsilon_t \}\) segue un modello autoregressivo a eteroschedasticità condizionata di ordine unitario, chiamato ARCH(1). Sostituendo \(\sigma^2_t\), otteniamo:
\(\begin{eqnarray} \epsilon_t = w_t \sqrt{\alpha_0 + \alpha_1 \epsilon_{t-1}^2}\end{eqnarray}\)
Perché scegliamo questo modello di volatilità?
Troviamo la definizione “formale” vista sopra poco motivata per introdurre la volatilità. Tuttavia, notiamo che la volatilità entra nella definizione semplicemente elevando al quadrato entrambi i lati dell’equazione:
\(\begin{eqnarray}
\operatorname{Var}(\epsilon_t) &=& \operatorname{E}[\epsilon^2_t ] – (\operatorname{E}[\epsilon_t ])^2 \\
&=& \operatorname{E}[\epsilon^2_t ] \\
&=& \operatorname{E}[w^2_t ] \operatorname{E}[\alpha_0 + \alpha_1 \epsilon^2_{t-1} ] \\
&=& \operatorname{E}[\alpha_0 + \alpha_1 \epsilon^2_{t-1} ] \\
&=& \alpha_0 + \alpha_1 \operatorname{Var}(\epsilon_{t-1})
\end{eqnarray}\)
Abbiamo applicato la definizione di varianza \(\operatorname{Var}(x) = \operatorname{E}[x^2] – (\operatorname{E}[x])^2\) e sfruttato la linearità dell’operatore E, oltre al fatto che \(\{w_t \}\) ha media zero e varianza unitaria.
Osserviamo che la varianza della serie risulta da una combinazione lineare della varianza dell’elemento precedente. In breve, la varianza di un processo ARCH(1) segue un processo AR(1).
Confrontiamo ora il modello ARCH(1) con un modello AR(1). Ricordiamo che quest’ultimo è definito come:
\(\begin{eqnarray} x_t = \alpha_0 + \alpha_1 x_{t-1} + w_t \end{eqnarray}\)
I modelli presentano una struttura simile, fatta eccezione per il termine legato al rumore bianco.
Quando usiamo ARCH(1)?
Quale strategia adottiamo per valutare l’idoneità di un modello ARCH(1) su una serie temporale?
Nel caso del modello AR(1), analizziamo il decadimento del primo ritardo nel correlogramma. Allo stesso modo, possiamo esaminare il quadrato dei residui per verificare se un modello AR(1) applicato ai residui quadrati risulti adatto. Questo ci suggerisce la presenza di un processo ARCH(1).
Applichiamo ARCH(1) solo a una serie per cui abbiamo già stimato un modello in grado di produrre residui simili a un rumore bianco discreto. Dato che verifichiamo l’adeguatezza di ARCH solo dopo aver elevato al quadrato i residui ed esaminato il correlogramma, ci assicuriamo che la media dei residui sia zero.
In sostanza, applichiamo ARCH solo a una serie priva di trend o stagionalità, ovvero senza evidenti correlazioni seriali. Dopo aver applicato un modello ARIMA (o ARIMA stagionale) a una serie del genere, otteniamo un buon punto di partenza per stimare ARCH.
I modelli ARCH(p)
Estendiamo facilmente il modello ARCH a ritardi di ordine superiore. Definiamo un processo ARCH(p) come:
\(\begin{eqnarray}\epsilon_t = w_t \sqrt{\alpha_0 + \sum^p_{i=1} \alpha_p \epsilon^2_{t-i}}\end{eqnarray}\)
Possiamo interpretare ARCH(p) come un modello AR(p) applicato alla varianza della serie.
Sorge spontanea la domanda: perché non applicare anche un modello MA(q) a media mobile, oppure un modello misto ARMA(p,q) alla varianza?
Questa riflessione ci conduce direttamente alla motivazione che ha portato allo sviluppo del modello ARCH generalizzato, noto come GARCH, che ora definiamo e descriviamo.
Modello Autoregressivo Generalizzato a
Eteroschedasticità Condizionata
Definizione
Modello autoregressivo generalizzato a eteroschedasticità condizionata di ordine p, q.
Definiamo una serie temporale \(\{ \epsilon_t \}\) a ogni istante come segue:
\(\begin{eqnarray}\epsilon_t = \sigma_t w_t\end{eqnarray}\)
In cui \(\{ w_t \}\) rappresenta un rumore bianco discreto con media zero e varianza unitaria, mentre \(\sigma^2_t\) segue la relazione:
\(\begin{eqnarray}\sigma^2_t = \alpha_0 + \sum^{q}_{i=1} \alpha_i \epsilon^2_{t-i} + \sum^{p}_{j=1} \beta_j \sigma^2_{t-j}\end{eqnarray}\)
Qui \(\alpha_i\) e \(\beta_j\) sono i parametri del modello.
Concludiamo quindi che \(\{ \epsilon_t \}\) rappresenta un modello autoregressivo generalizzato a eteroschedasticità condizionata di ordine p,q, noto come GARCH(p,q).
La definizione è simile a quella di ARCH(p), con l’aggiunta dei termini a media mobile: il valore di \(\sigma^2_t\) dipende anche dai precedenti \(\sigma^2_{t-j}\).
GARCH rappresenta quindi “l’equivalente ARMA” di ARCH, che include solo una componente autoregressiva.
Simulazioni, Correlogrammi e Stima del Modello
Come di consueto, partiamo dal modello più semplice: GARCH(1,1), che implica un ritardo autoregressivo e uno di media mobile. Il modello si scrive così:
\(\begin{eqnarray}
\epsilon_t &=& \sigma_t w_t \\
\sigma^2_t &=& \alpha_0 + \alpha_1 \epsilon^2_{t-1} + \beta_1 \sigma^2_{t-1}
\end{eqnarray}\)
Verifichiamo che \(\alpha_1 + \beta_1 < 1\), altrimenti la serie diventa instabile.
Il modello autoregressivo generalizzato a eteroschedasticità condizionata include tre parametri: \(\alpha_0\), \(\alpha_1\) e \(\beta_1\). Consideriamo i valori \(\alpha_0 = 0.2\), \(\alpha_1 = 0.5\) e \(\beta_1 = 0.3\).
Per implementare GARCH(1,1) in Python, seguiamo una procedura simile a quella usata per simulare una camminata casuale. Creiamo un vettore w per i valori di rumore bianco e un vettore eps separato per memorizzare i valori della serie temporale.
In questo caso, utilizziamo le funzioni di numpy per inizializzare un vettore di zeri, da riempire con i valori simulati secondo il modello GARCH.
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
np.random.seed(2)
a0 = 0.2
a1 = 0.5
b1 = 0.3
n = 10000
w = np.random.normal(0, 1, n)
eps = np.zeros(n)
sigsq = np.zeros(n)
for i in range(1, n):
sigsq[i] = a0 + a1 * (eps[i-1]**2) + b1 * sigsq[i-1]
eps[i] = w[i] * np.sqrt(sigsq[i])
A questo punto abbiamo generato il nostro modello GARCH utilizzando i suddetti parametri su 10.000 campioni. Siamo ora in grado di tracciare il correlogramma:
from statsmodels.graphics.tsaplots import plot_acf
import matplotlib.pyplot as plt
plot_acf(eps)
plt.show()
Si noti che la serie sembra la realizzazione di un processo di rumore bianco discreto:
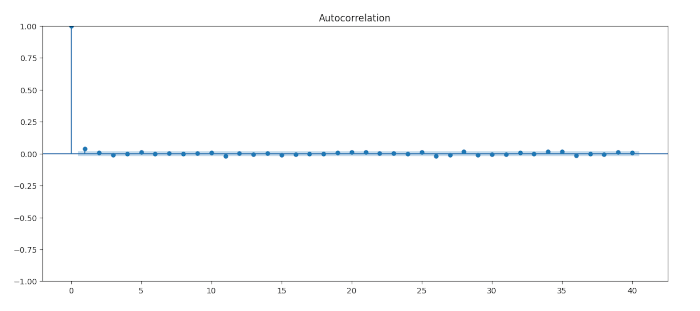
Tuttavia, se tracciamo il correlogramma del quadrato della serie:
plot_acf(eps**2)
plt.show()
Vediamo che si tratta sostanzialmente di un processo condizionalmente eteroschedastico attraverso il decadimento di ritardi successivi:
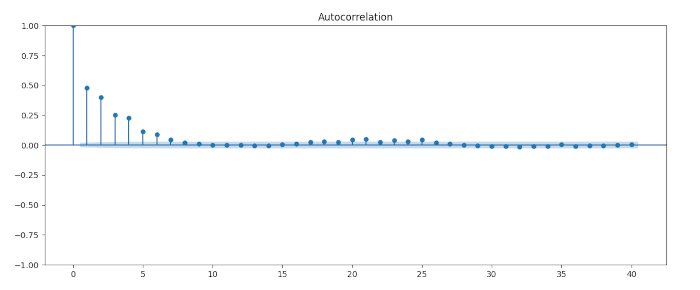
Come negli articoli precedenti, proviamo ad adattare un modello autoregressivo generalizzato a eteroschedasticità condizionata GARCH a questa serie simulata in modo da verificare se otteniamo gli stessi parametri della seria simulata. A tale scopo dobbiamo utilizzare la libreria arch di Python che fornisce la funzione arch_model per eseguire questa procedura:
from arch import arch_model
# Stimiamo un modello GARCH(1,1)
model = arch_model(eps, vol='GARCH', p=1, q=1)
res = model.fit(disp="off")
# Stampiamo l'intervallo di confidenza al 97.5%
print(res.summary())
conf_int = res.conf_int(alpha=0.05) # livello di confidenza 95%
print("Intervalli di confidenza al 97.5%:")
print(conf_int)
Constant Mean - GARCH Model Results
==============================================================================
Dep. Variable: y R-squared: 0.000
Mean Model: Constant Mean Adj. R-squared: 0.000
Vol Model: GARCH Log-Likelihood: -12237.3
Distribution: Normal AIC: 24482.6
Method: Maximum Likelihood BIC: 24511.4
No. Observations: 10000
Date: Df Residuals: 9999
Time: 19:47:40 Df Model: 1
Mean Model
==============================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------------
mu -6.7225e-03 6.735e-03 -0.998 0.318 [-1.992e-02,6.478e-03]
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
omega 0.2021 1.043e-02 19.383 1.084e-83 [ 0.182, 0.223]
alpha[1] 0.5162 2.016e-02 25.611 1.144e-144 [ 0.477, 0.556]
beta[1] 0.2879 1.870e-02 15.395 1.781e-53 [ 0.251, 0.325]
========================================================================
Covariance estimator: robust
Intervalli di confidenza al 97.5%:
lower upper
mu -0.019923 0.006478
omega 0.181658 0.222529
alpha[1] 0.476718 0.555729
beta[1] 0.251289 0.324610
Dati finanziari
Ora che sappiamo come simulare e adattare un modello autoregressivo generalizzato a eteroschedasticità condizionata GARCH, vogliamo applicare la procedura ad alcune serie finanziarie. In particolare, proviamo ad adattare ARIMA e GARCH all’indice S&P500 delle maggiori società statunitensi per capitalizzazione di mercato. Yahoo Finance utilizza il simbolo “^GSPC” per l’indice. Possiamo usare yfinance per ottenere i dati:
import numpy as np
import yfinance as yf
import pandas as pd
symbol = '^GSPC'
data = yf.download(symbol, start="2007-01-01", end="2015-10-01", group_by='ticker', auto_adjust=False)
sp500_data = data[symbol]
Possiamo quindi calcolare le differenze dei rendimenti logaritmici del prezzo di chiusura:
sp500_log_returns = np.log(sp500_data['Adj Close']).diff().dropna()
sp500_log_returns.index = pd.DatetimeIndex(sp500_log_returns.index).to_period("D")
E tracciare il grafico dei valori
import matplotlib.pyplot as plt
sp500_log_returns.plot()
plt.show()
È molto chiaro che ci sono periodi di aumento significativo della volatilità, in particolare intorno al 2008-2009, alla fine del 2011 e, più recentemente, a metà del 2015:
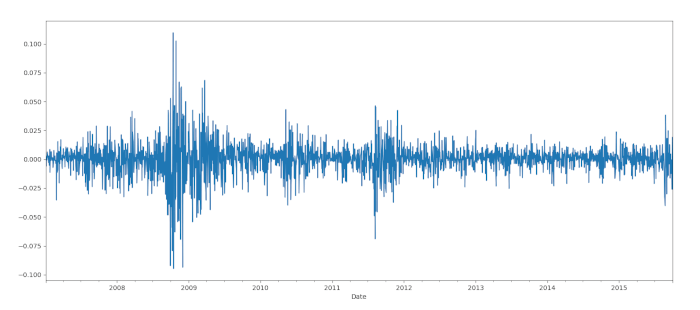
Il prossimo passo consiste nell’adattare un modello ARIMA(p,d,q). Abbiamo descritto il processo nella lezione precedente, quindi riportiamo direttamente il codice Python:
import pandas as pd
from statsmodels.tsa.arima_model import ARIMA
order_aic = []
# Loop over p values from 0-4
for p in range(5):
# Loop over d values from 0-1
for d in range(2):
# Loop over q values from 0-4
for q in range(5):
try:
# create and fit ARMA(p,q) model
model = ARIMA(LogRet, order=(p, d, q))
results = model.fit()
# Append order and results tuple
order_aic.append((p, d, q, results.aic, results))
except Exception as e:
print(str(e))
pass
# Construct DataFrame from order_aic
order_df = pd.DataFrame(order_aic, columns=['p', 'd', 'q', 'AIC', 'Results'])
# Get the result of best order model
best_result = order_df.sort_values('AIC').iloc[0]
print("p = ", best_result.p)
print("d = ", best_result.d)
print("q = ", best_result.q)
Dal momento che abbiamo già differenziato i rendimenti della serie SP500, otteniamo la componente integrata d uguale a zero, come previsto:
Ordine ARIMA ottimale: (2, 0, 1)
Otteniamo un modello ARIMA(2,0,1), ovvero due parametri autoregressivi e un parametro di media mobile.
Ora possiamo verificare se i residui di questo modello mostrano segni di eteroschedasticità condizionata. Per farlo, tracciamo il correlogramma dei residui
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
residuals = best_model.resid
plot_acf(residuals, lags=30)
plt.show()
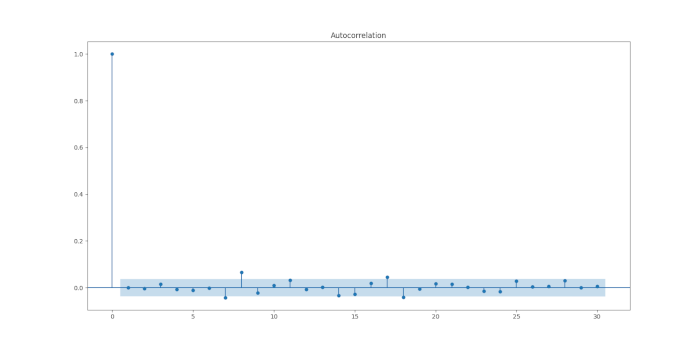
Il grafico appare come una realizzazione di un processo white noise discreto, indicando che il modello ARIMA(2,0,1) si adatta bene ai dati.
Per testare la presenza di eteroschedasticità condizionata, eleviamo al quadrato i residui e tracciamo il correlogramma:
squared_residuals = residuals**2
plot_acf(squared_residuals, lags=30)
plt.show()
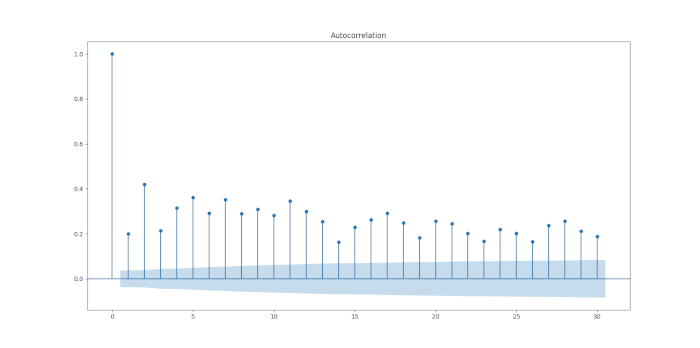
Osserviamo una chiara correlazione seriale nei residui quadratici, segno della presenza di eteroschedasticità condizionata nella serie dei log rendimenti dell’S&P 500.
A questo punto siamo in grado di adattare un modello autoregressivo generalizzato a eteroschedasticità condizionata GARCH utilizzando la libreria arch di Python
from arch import arch_model
# Stimiamo un modello GARCH(1,1)
garch_model = arch_model(sp500_log_returns, vol='GARCH', p=1, q=1)
garch_fit = garch_model.fit(disp='off')
Infine, per verificare il buon adattamento possiamo tracciare il correlogramma dei residui GARCH:
# Rimuove il primo valore NA dai residui
res = garch_fit.resid.dropna()
# ACF dei residui GARCH
plot_acf(res, lags=30)
plt.show()
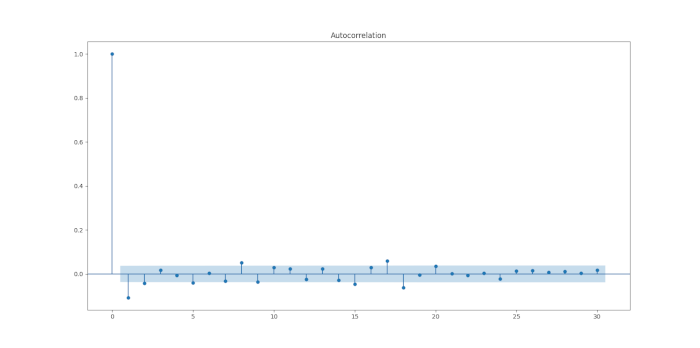
Il correlogramma sembra la realizzazione di un processo di rumore bianco discreto, che indica il buon adattamento del modello autoregressivo generalizzato a eteroschedasticità condizionata.
Ancora una volta, abbiamo quella che sembra la realizzazione di un processo di rumore bianco discreto, indicando che abbiamo “spiegato” la correlazione seriale presente nei residui con un’appropriata miscela di ARIMA(p,d,q) e GARCH(p, q).
Conclusioni
Finora abbiamo descritto come studiare le serie temporali applicando i modelli ARIMA e GARCH, consentendoci di adattare una combinazione di questi modelli a un indice del mercato azionario e di determinare se abbiamo raggiunto o meno un buon adattamento.
Il passaggio successivo consiste nel produrre effettivamente previsioni sui valori dei rendimenti giornalieri futuri tramite questo approccio e utilizzarlo per creare una strategia di trading di base.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

