In questa lezione introduciamo un’estensione del modello ARMA: il modello autoregressivo integrato a media mobile, ovvero il modello ARIMA(p,d,q). Consideriamo il modello ARIMA quando analizziamo serie non stazionarie, che si presentano in presenza di tendenze stocastiche.
Nelle precedenti lezioni abbiamo analizzato in dettaglio i modelli AR(p), MA(q) e ARMA(p,q). Abbiamo creato set di dati simulati, adattato i modelli per stimarne i parametri e infine applicato queste tecniche ai dati dei titoli finanziari.
Introduzione
Durante questo corso sviluppiamo costantemente lo studio delle serie temporali attraverso concetti come correlazione seriale, stazionarietà, linearità, residui, correlogrammi, simulazione, adattamento, stagionalità, eteroschedasticità condizionale e verifica delle ipotesi.
Finora non abbiamo generato previsioni dai nostri modelli e quindi non abbiamo creato un sistema di trading o una curva di equity.
Approfondiamo ARIMA in questa lezione e ci prepariamo ad affrontare ARCH e GARCH nelle prossime. In questo modo costruiremo una strategia di trading di base orientata al lungo termine, fondata sulla previsione dei rendimenti degli indici azionari.
Anche se i modelli AR, MA e ARMA non offrono grandi prestazioni nel trading, ora abbiamo una solida esperienza nella modellazione delle serie temporali.
Questo ci permette di affrontare modelli più avanzati e presenti nella letteratura accademica con una base di conoscenza utile a valutarli in modo efficace, evitando di considerarli come una “scatola nera”.
Ancora più importante, ci sentiamo pronti a modificarli ed estenderli con consapevolezza, sapendo esattamente cosa stiamo facendo!
Vi ringraziamo per aver seguito fin qui con pazienza, anche se può sembrare che queste lezioni si allontanino dall’azione concreta del trading. Tuttavia, sappiamo bene che la ricerca nel trading quantitativo richiede attenzione, rigore e molto tempo per raggiungere risultati validi. Non esistono scorciatoie o “schemi per arricchirsi” nel trading quantitativo.
Ora siamo quasi pronti a considerare il nostro primo modello di trading, che combinerà ARIMA e GARCH. Per questo, dedichiamo il tempo necessario a comprendere a fondo il modello ARIMA.
Dopo aver costruito il nostro primo modello, analizzeremo approcci più avanzati come i processi a memoria lunga, i modelli nello spazio degli stati (come il filtro di Kalman) e i modelli Vector Autoregressive (VAR), fondamentali per strategie di trading sofisticate.
Modello Autoregressivo Integrato a Media Mobile (ARIMA) di ordine p, d, q
Fondamento logico
Utilizziamo i modelli ARIMA per trasformare serie non stazionarie in stazionarie attraverso una serie di differenziazioni.
Come abbiamo descritto nella lezione sul rumore bianco e le passeggiate casuali, quando applichiamo l’operatore differenziale a una serie \(\{x_t \}\) otteniamo il rumore bianco \(\{w_t \}\):
\(\begin{eqnarray} \nabla x_t = x_t – x_{t-1} = w_t \end{eqnarray}\)
Il modello ARIMA applica questa operazione ripetutamente, d volte, per ottenere una serie stazionaria.
Per affrontare altre forme di non stazionarietà, oltre alle tendenze stocastiche, possiamo utilizzare modelli aggiuntivi.
Ad esempio, gestiamo la stagionalità con il modello SARIMA, mentre affrontiamo l’eteroschedasticità condizionale, come la volatilità aggregata negli indici azionari, con i modelli ARCH/GARCH.
In questa lezione analizziamo le serie non stazionarie con tendenze stocastiche, adattiamo i modelli ARIMA a queste serie e otteniamo previsioni per i dati finanziari.
Definizioni
Prima di definire il modello ARIMA, introduciamo il concetto di serie integrata:
Serie integrata di ordine d
Una serie \(\{x_t \}\) è integrata di ordine \(I(d)\) se:\(\begin{eqnarray}\nabla^d x_t = w_t \end{eqnarray}\)
Cioè, se differenziamo la serie d volte otteniamo una serie di rumore bianco.
In alternativa, utilizzando l’operatore di spostamento all’indietro B:
\(\begin{eqnarray}(1-{\bf B}^d) x_t = w_t \end{eqnarray} \)
Ora possiamo definire il modello ARIMA:
Modello Autoregressivo Integrato a Media Mobile di ordine p, d, q
Una serie \(\{x_t \}\) segue un modello ARIMA(p,d,q) se \(\nabla^d x_t\) segue un processo ARMA(p,q).In altre parole, se differenziamo la serie d volte e otteniamo un processo ARMA(p,q), allora abbiamo un modello ARIMA(p,d,q).
Con la notazione polinomiale per il modello AR e il modello MA, possiamo scrivere ARIMA(p,d,q) con l’operatore B:
\(\begin{eqnarray}\theta_p({\bf B})(1-{\bf B})^d x_t = \phi_q ({\bf B}) w_t\end{eqnarray}\)
Dove \(w_t\) è una serie di rumore bianco.
Notiamo alcuni aspetti importanti di queste definizioni.
Poiché la passeggiata casuale è data da \(x_t = x_{t-1} + w_t\), possiamo vedere che \(I(1)\) rappresenta una differenziazione prima, cioè \(\nabla^1 x_t = w_t\).
Quando sospettiamo una tendenza non lineare, applichiamo differenziazioni multiple (es. \(d > 1\)) per trasformare la serie in rumore bianco stazionario.
In Python possiamo usare il comando diff della libreria Pandas, specificando parametri come l’intervallo, per differenziare ripetutamente.
Simulazione, Correlogramma e Model Fitting
Applichiamo una procedura simile a quella descritta nella lezione sul modello ARMA. La differenza principale sta nell’impostare \(d=1\), per ottenere una serie non stazionaria con una componente di trend stocastico.
Adattiamo un modello ARIMA ai nostri dati simulati, stimiamo i parametri, calcoliamo intervalli di confidenza, produciamo un correlogramma dei residui del modello e infine eseguiamo il test di Ljung-Box per valutare la bontà dell’adattamento.
Simuliamo un modello ARIMA(1,1,1), con il coefficiente autoregressivo \(\alpha=0.6\) e il coefficiente di media mobile \(\beta=-0.5\). Di seguito il codice Python per simulare e tracciare questa tipologia di serie:
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
# Imposta il seed per la riproducibilità
np.random.seed(1)
# Specifica i parametri ARIMA(1,1,1)
ar = np.array([1, -0.6]) # AR(1) con coefficiente 0.6
ma = np.array([1, -0.5]) # MA(1) con coefficiente -0.5
# Simula un processo ARMA(1,1)
arma_process = ArmaProcess(ar, ma)
x_diff = arma_process.generate_sample(nsample=1000)
# Integra la serie per ottenere ARIMA(1,1,1)
x = np.cumsum(x_diff)
# Plot della serie simulata
plt.plot(x)
plt.show()
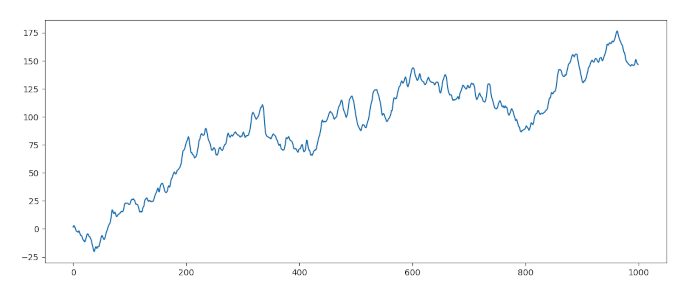
Ora che abbiamo la serie simulata, proviamo ad adattare un modello autoregressivo integrato a media mobile ARIMA(1,1,1). Dato che conosciamo l’ordine, possiamo semplicemente specificarlo nell’adattamento:
from statsmodels.tsa.arima.model import ARIMA
# Stima del modello ARIMA(1,1,1)
model = ARIMA(x, order=(1, 1, 1))
x_arima = model.fit()
# Sommario dei risultati
print(x_arima.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARIMA(1, 1, 1) Log Likelihood -1397.888
Date: AIC 2801.776
Time: 18:00:17 BIC 2816.496
Sample: 0 HQIC 2807.371
- 1000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.5962 0.212 2.814 0.005 0.181 1.011
ma.L1 -0.5139 0.225 -2.280 0.023 -0.956 -0.072
sigma2 0.9614 0.041 23.405 0.000 0.881 1.042
===================================================================================
Ljung-Box (L1) (Q): 0.12 Jarque-Bera (JB): 3.41
Prob(Q): 0.73 Prob(JB): 0.18
Heteroskedasticity (H): 1.00 Skew: -0.07
Prob(H) (two-sided): 0.99 Kurtosis: 3.25
===================================================================================
# Intervalli di confidenza al 95%
ar1 = x_arima.params[0]
ma1 = x_arima.params[1]
se_ar1 = x_arima.bse[0]
se_ma1 = x_arima.bse[1]
ci_ar1 = ar1 + np.array([-1.96, 1.96]) * se_ar1
ci_ma1 = ma1 + np.array([-1.96, 1.96]) * se_ma1
print("IC 95% AR(1):", ci_ar1)
print("IC 95% MA(1):", ci_ma1)
IC 95% AR(1): [0.18096677 1.01148484]
IC 95% MA(1): [-0.9555749 -0.07215328]
Entrambe le stime dei parametri rientrano negli intervalli di confidenza e sono vicine ai valori reali dei parametri della serie ARIMA simulata. Quindi, non dovremmo essere sorpresi di vedere i residui che sembrano una realizzazione di rumore bianco discreto:
# Correlogramma dei residui
from statsmodels.graphics.tsaplots import plot_acf
residuals = x_arima.resid
plot_acf(residuals)
plt.show()
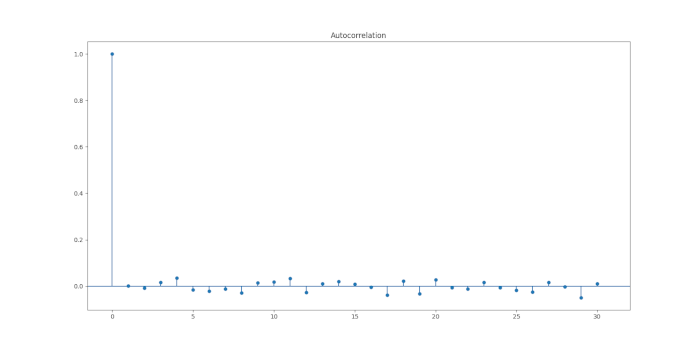
Infine, possiamo eseguire un test Ljung-Box per fornire le prove statistiche di un buon adattamento:
from statsmodels.stats.diagnostic import acorr_ljungbox
ljung_box = acorr_ljungbox(residuals, lags=[20], return_df=True)
print(ljung_box)
lb_stat lb_pvalue
19.783933 0.471517
Possiamo vedere che il valore p è significativamente maggiore di 0,05 e come tale possiamo affermare che ci sono prove evidenti che il rumore bianco discreto si adatti bene ai residui. Quindi, il modello ARIMA(1,1,1) è adatto, come previsto.
Previsione delle Serie Finanziari
Vediamo ora come adattare il modello autoregressivo integrato a media mobile ARIMA ad Amazon, Inc. (AMZN) e all’indice S&P500 US Equity (^GPSC, in Yahoo Finance). Usiamo la libreria StatsModels di Python.
Analisi titolo Amazon
Iniziamo usando yfinance per scaricare le serie dei prezzi giornalieri di Amazon dall’inizio del 2013. Inoltre calcoliamo i differenziali di primo ordine delle serie, in questo modo l’adattamento al modello ARIMA non richiede \(d > 0\) per il componente integrato:
import numpy as np
import yfinance as yf
import pandas as pd
symbol = 'AMZN'
data = yf.download(symbol, start="2013-01-01")
data = data.asfreq('b').fillna(method='ffill')
data['Return'] = data['Adj Close'].pct_change()
data['LogRet'] = np.log(data['Adj Close']).diff()
Come nella 3° parte della serie di articoli su modelli ARMA, analizziamo le combinazioni di \(p\), \(d\) e \(q\), per trovare il modello ARIMA(p,d,q) ottimale. Per “ottimale” si intende la combinazione di ordini che riduce al minimo l’Akaike Information Criterion (AIC):
from statsmodels.tsa.arima.model import ARIMA
amzn_diff = data['LogRet']
best_aic = np.inf
best_order = None
best_model = None
for p in range(1, 5):
for d in range(0, 2):
for q in range(1, 5):
try:
model = ARIMA(amzn_diff, order=(p, d, q))
result = model.fit()
if result.aic < best_aic:
best_aic = result.aic
best_order = (p, d, q)
best_model = result
except:
continue
print("Ordine ARIMA ottimale:", best_order)
Possiamo vedere che è stato selezionato un ordine di \(p=3\), \(d=0\), \(q=3\). In particolare si conferma \(d=0\) dato che abbiamo già considerato le differenze di primo ordine nella serie in ingresso.
Ordine ARIMA ottimale: (3, 0, 3)
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
residuals = best_model.resid
plot_acf(residuals, lags=30)
plt.show()
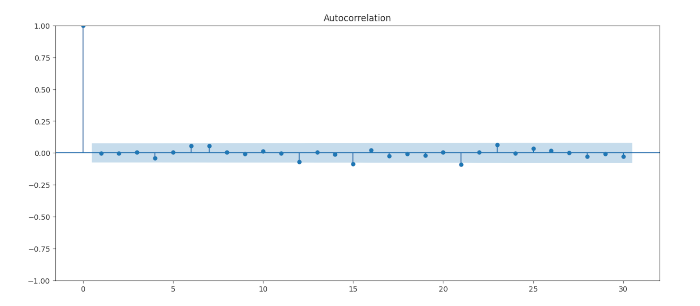
Anche se dobbiamo aspettarci la presenza di picchi statisticamente significativi semplicemente a causa della variabilità campionaria nel 5% dei casi.
Eseguiamo ora un test di Ljung-Box per verificare se abbiamo evidenza di un buon adattamento del modello:
# Test di Ljung-Box sui residui
from statsmodels.stats.diagnostic import acorr_ljungbox
ljung_box = acorr_ljungbox(residuals, lags=[20], return_df=True)
print(ljung_box)
lb_stat lb_pvalue
11.77952 0.923456
Come possiamo vedere, il valore p è maggiore di 0,05 e quindi abbiamo prove di un buon adattamento al livello del 95%.
Ora possiamo utilizzare il comando forecast per prevedere con alcuni giorni di anticipo la serie finanziaria di Amazon:
# Crea intervallo con frequenza giornaliera
last_date = amzn_log_returns.index[-1].to_timestamp()
forecast_dates = pd.date_range(start=last_date + pd.Timedelta(days=1), periods=25, freq='D')
# Previsione
forecast_result = best_model.get_forecast(steps=25)
forecast_mean = forecast_result.predicted_mean
conf_int = forecast_result.conf_int(alpha=0.05)
# Assegna indice alle previsioni
forecast_mean.index = forecast_dates
conf_int.index = forecast_dates
plt.figure(figsize=(10, 5))
plt.plot(amzn_log_returns.index.to_timestamp(), amzn_log_returns, label='Serie Storica')
plt.plot(forecast_mean.index, forecast_mean, label='Previsione')
plt.fill_between(conf_int.index, conf_int.iloc[:, 0], conf_int.iloc[:, 1],
color='blue', alpha=0.2, label='Intervallo 95%')
plt.legend()
plt.title("Previsione a 25 giorni dei ritorni logaritmici di AMZN")
plt.show()
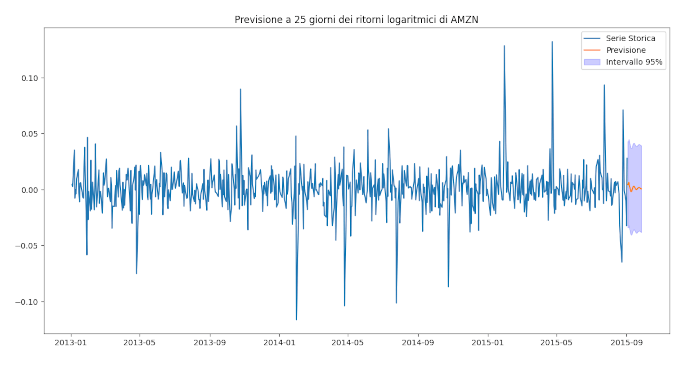
Notiamo che le previsioni puntuali per i prossimi giorni con bande di errore del 95%. Utilizzeremo queste previsioni nella nostra prima strategia di trading di serie temporali quando arriveremo a combinare il modello autoregressivo integrato a media mobile ARIMA e GARCH.
Analisi indice S&P500
Eseguiamo la stessa procedura per l’S&P500. Per prima cosa otteniamo i dati da yfinance e li convertiamo in un flusso di rendimenti logaritmici:
import numpy as np
import yfinance as yf
import pandas as pd
symbol = '^GSPC'
data = yf.download(symbol, start="2013-01-01", end="2015-09-03", group_by='ticker', auto_adjust=False)
sp500_data = data[symbol]
sp500_log_returns = np.log(sp500_data['Close']).diff().dropna()
sp500_log_returns.index = pd.DatetimeIndex(sp500_log_returns.index).to_period("D")
Fittiamo un modello ARIMA eseguendo un ciclo sui valori di p, d e q:
from statsmodels.tsa.arima.model import ARIMA
best_aic = np.inf
best_order = None
best_model = None
for p in range(1, 5):
for d in range(0, 2):
for q in range(1, 5):
try:
model = ARIMA(sp500_log_returns, order=(p, d, q))
result = model.fit()
if result.aic < best_aic:
best_aic = result.aic
best_order = (p, d, q)
best_model = result
except:
continue
print("Ordine ARIMA ottimale:", best_order)
L’AIC ci dice che il modello “migliore” è il modello autoregressivo integrato a media mobile ARIMA(4,0,1). Da notare ancora una volta che d=0, poiché abbiamo già considerato le differenze di primo ordine della serie:
Ordine ARIMA ottimale: (4, 0, 1)
Possiamo tracciare i residui del modello adattato per verificare se otteniamo un rumore bianco discreto:
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
residuals = best_model.resid
plot_acf(residuals, lags=30)
plt.show()
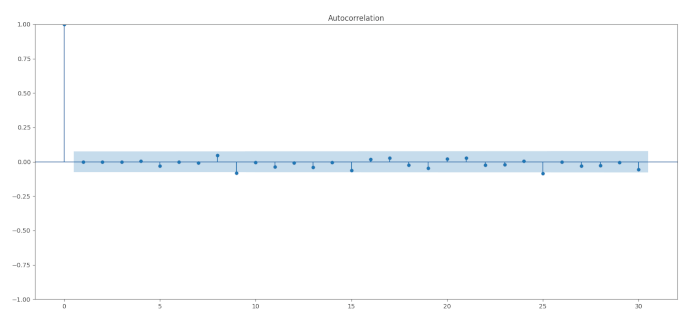
Il correlogramma sembra promettente, quindi il passo successivo è eseguire il test Ljung-Box e confermare che abbiamo un buon adattamento del modello:
# Test di Ljung-Box sui residui
from statsmodels.stats.diagnostic import acorr_ljungbox
ljung_box = acorr_ljungbox(residuals, lags=[20], return_df=True)
print(ljung_box)
lb_stat lb_pvalue
14.326806 0.813547
Poiché il p-value è maggiore di 0,05, abbiamo verificato il buon adattamento del modello.
Nella lezione precedente il test Ljung-Box per l’S&P500 ha mostrato che l’ARMA(3,3) non era adatto ai rendimenti giornalieri logaritmici.
In questa analisi abbiamo deliberatamente troncato i dati dell’S&P500 per iniziare dal 2013 in poi , che esclude convenientemente i periodi volatili intorno al 2007-2008. Quindi abbiamo escluso gran parte dell’S&P500 dove avevamo un eccessivo cluster di volatilità. Ciò influisce sulla correlazione seriale della serie e quindi ha l’effetto di far sembrare la serie “più stazionaria” rispetto al passato.
Questo è un punto fondamentale. Quando analizziamo serie storiche, dobbiamo prestare estrema attenzione alla eteroschedasticità condizionata, una caratteristica comune negli indici di borsa. In finanza quantitativa, identificare periodi con diversa volatilità è noto come regime detection – un compito complesso e delicato.
Descriviamo a fondo questo aspetto nella prossima lezione, quando introdurremo i modelli ARCH e GARCH.
Tracciamo ora una previsione per i prossimi giorni dei rendimenti del registro giornaliero dell’S&P500:
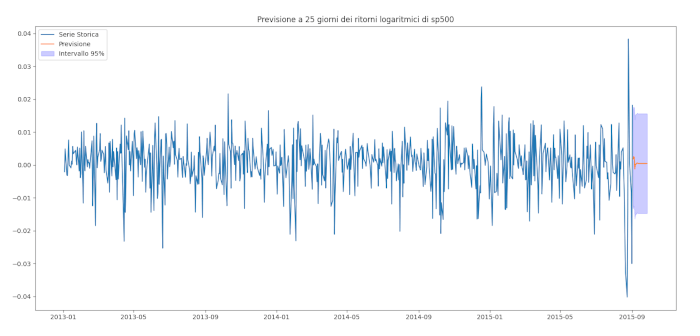
Conclusioni
Ora che abbiamo la capacità di adattare e prevedere il modello autoregressivo integrato a media mobile ARIMA, siamo molto vicini alla possibilità di creare indicatori per una strategia di trading.
Dobbiamo descrivere il modello Generalized Autoregressive Conditional Heteroscedasticity (GARCH) e usarlo per spiegare meglio la correlazione seriale in alcune serie di titoli azionari e serie di indici azionari.
Dopo aver descritto il GARCH, saremo in grado di combinarlo con il modello ARIMA e creare indicatori di segnale e quindi una strategia base di trading quantitativo.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“