In questa lezione esploriamo come usare la correlazione seriale nei primi modelli di analisi delle serie temporali, inclusi alcuni semplici modelli stocastici lineari. In particolare, presentiamo il White Noise e Random Walks.
Obiettivo dell’analisi delle serie temporali
Prima di affrontare le definizioni, vogliamo riassumere le motivazioni per studiare questi modelli e chiarire l’obiettivo dello studio delle serie temporali.
Il nostro scopo principale consiste nel migliorare la redditività degli algoritmi di trading. In quanto analisti quantitativi, evitiamo “supposizioni” o “intuizioni”.
Adottiamo un approccio volto a quantificare il più possibile, per eliminare il coinvolgimento emotivo nel processo di trading e garantire (per quanto possibile) la ripetibilità delle operazioni.
Per aumentare la redditività dei nostri modelli, applichiamo tecniche statistiche che ci permettono di identificare comportamenti ricorrenti in strumenti specifici, così da sfruttarli per generare profitto. Per individuare questi pattern, analizziamo come le proprietà dei prezzi degli asset evolvono nel tempo.
L’analisi delle serie temporali ci aiuta a raggiungere questo obiettivo. Ci fornisce una struttura statistica solida per valutare il comportamento delle serie temporali, come i prezzi degli asset, con l’obiettivo di costruire strategie che ne traggano vantaggio.
L’analisi delle serie temporali ci fornisce un solido quadro statistico per valutare il comportamento dei prezzi degli asset.
Finora abbiamo approfondito la correlazione seriale e analizzato la struttura di correlazione dei dati simulati. Inoltre, abbiamo introdotto la stazionarietà e discusso le proprietà di secondo ordine delle serie temporali. Tutti questi aspetti ci aiutano a riconoscere i modelli presenti nelle serie. Se non hai ancora letto la lezione precedente sulla correlazione seriale, ti invitiamo a farlo prima di proseguire.
Ora vediamo come sfruttare la struttura dei prezzi degli asset che abbiamo individuato attraverso i modelli di serie temporali.
Processo di modellazione delle serie storiche
Che cos’è un modello di serie temporale? In sostanza, si tratta di un modello matematico che tenta di spiegare la correlazione seriale presente in una serie temporale.
Quando parliamo di “spiegare”, intendiamo che il modello che adattiamo a una serie temporale deve considerare alcune o tutte le correlazioni seriali presenti nel correlogramma. Cioè, adattando il modello alla serie, riduciamo la correlazione seriale.
Nel nostro ruolo di ricercatori quantitativi, analizziamo un’ampia gamma di modelli, tenendo conto delle loro ipotesi e complessità, e selezioniamo quello più semplice in grado di spiegare la correlazione seriale.
Una volta definito il modello, lo utilizziamo per prevedere i valori futuri o, più in generale, il comportamento futuro. Questa previsione risulta estremamente utile nel trading quantitativo.
Se riusciamo a prevedere la direzione del movimento di un asset, possiamo costruire una strategia di trading (ovviamente considerando i costi di transazione!). Inoltre, se stimiamo la volatilità di un asset, possiamo applicare un’altra strategia o un approccio di gestione del rischio. Ecco perché studiamo le proprietà di secondo ordine: ci aiutano a elaborare previsioni.
Valutazione dei modelli
Dobbiamo anche chiederci: “Come possiamo valutare la bontà di un modello?” Quali criteri usiamo per stabilire quale modello risulta il migliore? Esistono diversi criteri, che analizzeremo nel corso di questa serie di lezioni.
Riassumiamo il processo generale che seguiamo:
- Formuliamo un’ipotesi sul comportamento di una serie temporale specifica
- Generiamo il correlogramma della serie (con librerie Python) e analizziamo la sua correlazione seriale
- Applichiamo le nostre conoscenze sui modelli di serie temporali e adattiamo un modello adeguato per ridurre la correlazione seriale nei residui (vedi sotto per la definizione) del modello e della serie
- Affiniamo l’adattamento finché non eliminiamo le correlazioni e valutiamo il modello con criteri matematici
- Usiamo il modello e le sue proprietà di secondo ordine per fare previsioni sui valori futuri
- Valutiamo l’accuratezza delle previsioni con tecniche statistiche (come matrici di confusione, curve ROC per la classificazione, oppure metriche regressive come MSE, MAPE ecc.)
- Iteriamo questo processo finché non otteniamo la precisione desiderata, poi utilizziamo le previsioni per costruire strategie di trading
Questo rappresenta il nostro processo di base. La complessità aumenterà quando introdurremo modelli più avanzati che considerano correlazioni seriali aggiuntive nelle serie temporali.
White Noise e Random Walks
In questa lezione analizziamo due modelli di serie temporali fondamentali: il White Noise e Random Walks. Questi modelli costituiscono le basi dei successivi modelli più avanzati, quindi è fondamentale comprenderli a fondo.
Tuttavia, prima di presentarli, introduciamo alcuni concetti più astratti che ci aiuteranno a unificare il nostro approccio alla modellazione delle serie. In particolare, definiamo l’operatore di spostamento all’indietro e l’operatore di differenza.
Operatori di spostamento all’indietro e di differenza
Nella lezione introduciamo l’operatore di spostamento all’indietro (BSO) e l’operatore di differenza, strumenti fondamentali per scrivere diversi modelli di serie temporali in modo coerente, così da comprendere meglio le loro differenze.
Poiché useremo spesso queste notazioni, conviene definirle fin da subito.
Operatore di spostamento all’indietro
Indichiamo l’operatore di spostamento all’indietro, o di ritardo, con \({\bf B}\). Applicandolo a un elemento della serie temporale, otteniamo il valore osservato un’unità di tempo prima: \({\bf B} x_t = x_{t-1}\).
Applicando l’operatore più volte, torniamo indietro di \(n\) periodi: \({\bf B}^n x_t = x_{t-n}\).
In seguito, useremo il BSO per costruire gran parte dei nostri modelli di serie temporali.
Quando lavoriamo con serie non stazionarie (cioè con media e varianza che cambiano nel tempo), adottiamo una procedura di differenziazione per trasformarle in serie stazionarie.
Operatore differenza
L’operatore differenza, \(\nabla\), calcola la differenza tra un elemento della serie temporale e il suo valore precedente: \(\nabla x_t = x_t – x_{t-1}\) oppure \(\nabla x_t = (1 – {\bf B}) x_t\).
Come per il BSO, applichiamo ripetutamente anche questo operatore: \(\nabla^n = (1 – {\bf B})^n\).
Dopo aver introdotto questi operatori astratti, iniziamo a studiare modelli di white noise e random walks nelle serie temporali.
White Noise
Iniziamo con il concetto di rumore bianco, una base essenziale nella costruzione dei modelli.
Abbiamo già visto che cerchiamo di adattare i modelli alla serie temporale finché le componenti residue non mostrano correlazione seriale. Questo ci porta a definire la serie degli errori residui:
Serie dei residui
La serie degli errori residui (o residui), \(x_t\), rappresenta la differenza tra un valore osservato e uno previsto in un determinato istante \(t\).
Se \(y_t\) è il valore osservato e \(\hat{y}_t\) quello previsto, otteniamo: \(x_t = y_t – \hat{y}_t\).
Verifichiamo se il modello spiega la correlazione seriale delle osservazioni: se ci riesce, i residui risultano non correlati nel tempo.
Questo implica che ogni elemento dei residui rappresenta una realizzazione indipendente della stessa distribuzione di probabilità. In altre parole, i residui risultano indipendenti e identicamente distribuiti (iid).
Per costruire modelli in grado di spiegare la correlazione seriale, iniziamo da un processo che genera variabili casuali indipendenti. Così introduciamo il concetto di rumore bianco discreto:
Rumore bianco discreto
Consideriamo una serie temporale \(\{w_t: t=1,…n\}\). Se ogni elemento \(w_i\) risulta indipendente, identicamente distribuito con media zero, varianza \(\sigma^2\) e assenza di correlazione seriale (ossia \(\text{Cor}(w_i, w_j) = 0, \forall i \neq j\)), allora definiamo la serie come rumore bianco discreto (DWN).
Se gli elementi \(w_i\) provengono da una distribuzione normale standard (ossia \(w_t \sim N(0, \sigma^2)\)), chiamiamo la serie rumore bianco gaussiano.
Il white noise e random walks rappresentano strumenti utili in molti contesti. In particolare, usiamo il white noise per simulare serie sintetiche.
Poiché una serie storica rappresenta solo una realizzazione osservata, generiamo più realizzazioni per ottenere “molte storie”. Questo ci permette di stimare parametri di diversi modelli, perfezionare la loro struttura e migliorare la precisione nelle previsioni.
Dopo aver definito il Discrete White Noise, analizziamo ora alcune sue caratteristiche fondamentali, incluse le proprietà di secondo ordine e il correlogramma.
Proprietà di secondo ordine
Le proprietà di secondo ordine del DWN emergono direttamente dalla definizione. La media della serie è zero e non esiste autocorrelazione:
\(\begin{eqnarray} \mu_w = E(w_t) = 0 \end{eqnarray}\)
\(\rho_k = \text{Cor}(w_t, w_{t+k}) = \left\{\begin{aligned} &1 && \text{se} \enspace k = 0 \\ &0 && \text{se} \enspace k \neq 0 \end{aligned} \right.\)
Correlogramma
Possiamo rappresentare il correlogramma di un DWN utilizzando Python. Prima fissiamo un seme casuale pari a 1 per rendere ripetibili i risultati. Poi campioniamo 1000 elementi da una distribuzione normale e tracciamo l’autocorrelazione:
import numpy as np
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import acf
np.random.seed(1)
whiteNoise = np.random.standard_normal(1000)
plt.figure(figsize=[10, 7.5]); # Dimensioni del grafico
plt.plot(whiteNoise)
plt.title("Simulated White Noise")
plt.show()
acf_coef = acf(whiteNoise)
plot_acf(acf_coef, lags=30)
plt.show()
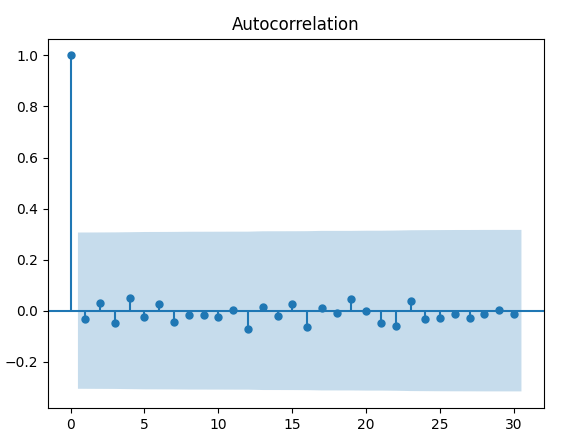
Notiamo che a \( k = 4 \), \( k = 12 \) e \( k = 16 \), abbiamo tre picchi che differiscono da zero per un livello del 5%. Tuttavia, questo è facilmente prevedibile a causa della variazione del campionamento dalla distribuzione normale.
Ancora una volta, dobbiamo essere estremamente attenti nell’interpretazione dei risultati. In questo caso, ci aspettiamo davvero che accada qualcosa di fisicamente significativo per \( k = 4 \), \( k = 12 \) o \( k = 16 \)?
Evidenziamo che il modello DWN ha un solo parametro, vale a dire la varianza \( \sigma^2 \). Per fortuna, è semplice stimare la varianza con Python, possiamo semplicemente usare la funzione var della libreria Numpy:
var = np.var(whiteNoise)
print(var)
Abbiamo definito il white noise come una distribuzione normale con media pari a 0 e deviazione standard pari a 1 (quindi varianza pari a 1). Python calcola la varianza campionaria come 0.962369, un valore molto vicino all’ideale di 1.
Utilizziamo il Discrete White Noise come modello di riferimento per i residui. Quando adattiamo modelli di serie temporali alle nostre osservazioni, ci serviamo del DWN per verificare di aver eliminato ogni correlazione seriale rimanente nei residui e quindi di aver ottenuto un buon adattamento del modello.
Dopo aver esplorato il DWN, introduciamo un modello molto noto per alcune serie temporali finanziarie: il Random Walk.
Random Walks
Una passeggiata casuale rappresenta un altro modello di serie temporale in cui l’osservazione corrente deriva da quella precedente con un incremento o decremento casuale. Definiamo formalmente questo modello come segue:
Passeggiata casuale
Una passeggiata casuale è un modello di serie temporale \( {x_t} \) tale che \( x_t = x_{t-1} + w_t \), dove \( w_t \) rappresenta una serie di rumore bianco discreto.
In precedenza abbiamo introdotto l’operatore di spostamento all’indietro \( {\bf B} \). Applichiamo ora il BSO alla passeggiata casuale:
\(\begin{eqnarray} x_t = {\bf B} x_t + w_t = x_{t-1} + w_t \end{eqnarray}\)
Eseguendo un ulteriore passo indietro:
\(\begin{eqnarray} x_{t-1} = {\bf B} x_{t-1} + w_{t-1} = x_{t-2} + w_{t-1} \end{eqnarray}\)
Se ripetiamo questo processo fino a coprire l’intera serie temporale, otteniamo:
\(\begin{eqnarray} x_t = (1 + {\bf B} + {\bf B}^2 + \ldots) w_t \end{eqnarray}\)
che equivale a:
\( x_t = w_t + w_{t-1} + w_{t-2} + \ldots\)
Risulta quindi evidente che la passeggiata aleatoria rappresenta la somma cumulativa degli elementi di una serie di rumore bianco discreto.
Proprietà di secondo ordine
Le proprietà di secondo ordine della passeggiata aleatoria risultano più interessanti rispetto a quelle del rumore bianco discreto. Anche se la media rimane zero, notiamo che la covarianza dipende dal tempo. Per questo motivo, una passeggiata aleatoria non è stazionaria:
\(\begin{eqnarray}\mu_x &=& 0 \\ \gamma_k (t) &=& \text{Cov}(x_t, x_{t+k}) = t \sigma^2 \end{eqnarray}\)
In pratica, la covarianza equivale alla varianza moltiplicata per il tempo. All’aumentare del tempo, cresce anche la varianza.
Che cosa comporta questo per le passeggiate casuali? In termini semplici, significa che proiettare “trend” a lungo termine ha poco senso, dato che si tratta letteralmente di processi casuali.
Correlogramma
Definiamo l’autocorrelazione di una passeggiata casuale (anch’essa dipendente dal tempo) con la seguente formula:
\(\begin{eqnarray} \rho_k (t) = \frac{\text{Cov}(x_t, x_{t+k})} {\sqrt{\text{Var}(x_t) \text{Var}(x_{t+k})}} = \frac{t \sigma^2}{\sqrt{t \sigma^2 (t+k) \sigma^2}} = \frac{1}{\sqrt{1+k/t}} \end{eqnarray}\)
Considerando una lunga serie temporale e ritardi a breve termine, otteniamo un’autocorrelazione prossima all’unità. In altre parole, rileviamo un’autocorrelazione molto elevata che decresce lentamente all’aumentare del ritardo. Possiamo simulare una serie di questo tipo con Python.
Per prima cosa impostiamo un seed per poter replicare esattamente i risultati. Quindi generiamo due sequenze di numeri casuali (\( x \) e \( w \)) che condividono lo stesso valore iniziale (dato dal seed).
Poi eseguiamo un ciclo su ogni elemento di \( x \) e assegniamo a ciascuno la somma dell’elemento precedente di \( x \) e del valore corrente di \( w \). Così otteniamo una passeggiata casuale. Infine tracciamo i risultati con type="l" per produrre un grafico a linee, evitando punti circolari.
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
steps = np.random.standard_normal(1000)
steps[0] = 0
random_walk = np.cumsum(steps)
plt.figure(figsize=[10, 7.5]); # Dimensioni del grafico
plt.plot(random_walk)
plt.title("Simulated Random Walk")
plt.show()
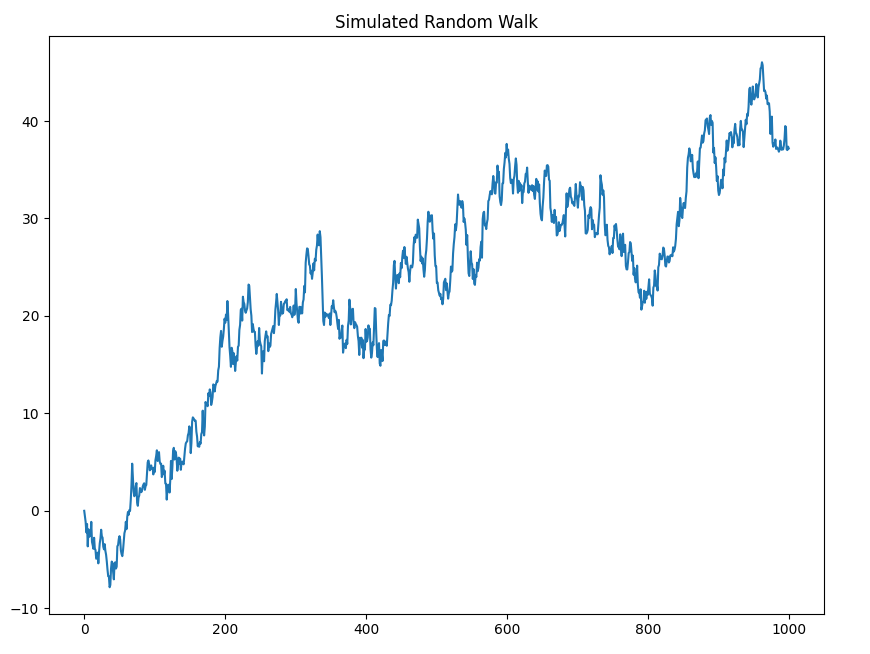
Possiamo visualizzare il correlogramma:
random_walk_acf_coef = acf(random_walk)
plot_acf(random_walk, lags=20)
plt.show()
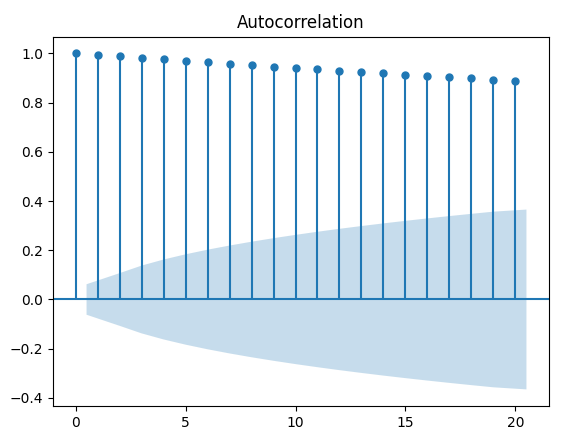
Adattamento dei Modelli di Random Walk ai dati Finanziari
Come abbiamo spiegato nella lezione precedente, dobbiamo quindi adattare i modelli ai dati che abbiamo già simulato.
Questa procedura appare chiaramente un po’ artificiale, dato che abbiamo simulato anche la random walk. Tuttavia, rappresenta uno strumento utile per comprendere le basi del processo di adattamento. Nelle situazioni reali non conosciamo il modello di generazione dei dati dello strumento sottostante, quindi possiamo solo adattare i modelli e valutarne il correlogramma.
Abbiamo sottolineato quanto questo approccio semplifichi il controllo della corretta implementazione del modello, cercando di mantenere le stime dei parametri vicine a quelle usate nelle simulazioni.
Adattamento ai dati simulati
Poiché dedicheremo molto tempo all’adattamento dei modelli alle serie temporali finanziarie, iniziamo con i dati simulati per esercitarci e prepararci al lavoro sui dati reali.
Abbiamo già generato una random walk aleatoria e possiamo utilizzare questa realizzazione per verificare se il modello proposto (per un processo aleatorio) descrive accuratamente i dati.
Come possiamo verificare che il modello ipotizzato per la random walk si adatti ai dati simulati? Bene, sfruttiamo la definizione di processo aleatorio: la differenza tra due valori vicini dovrebbe seguire un processo di rumore bianco discreto.
Creiamo quindi una serie di differenze dagli elementi della nostra serie simulata e otteniamo una sequenza che dovrebbe somigliare al rumore bianco discreto. Questo passaggio ci aiuta anche a comprendere la relazione tra white noise e random walks.
In Python, applichiamo facilmente questa logica usando la funzione diff. Dopo aver creato la serie delle differenze, stampiamo il grafico del correlogramma e valutiamo quanto si avvicini a un rumore bianco discreto.
random_walk_diff = np.diff(random_walk, n=1)
random_walk_diff_acf_coef = acf(random_walk_diff)
plot_acf(random_walk_diff, lags=20);
plt.show()
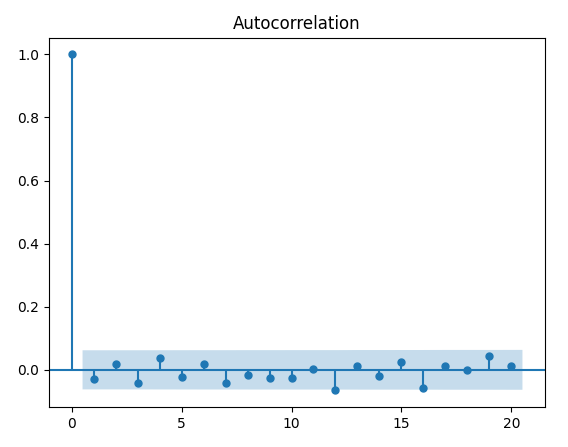
Cosa notiamo da questo grafico? Troviamo un picco statisticamente significativo per \( k = 12 \), ma solo in modo marginale. Ricordiamo che ci aspettiamo almeno il 5% dei picchi con significatività statistica, a causa della naturale variazione nel campionamento.
Possiamo quindi affermare con ragionevolezza che il correlogramma assomiglia a quello di un rumore bianco discreto. Questo significa che il modello di random walk si adatta bene ai nostri dati simulati. E proprio questo risultato ci aspettavamo, dato che inizialmente abbiamo simulato una random walk!
Adattamento ai dati finanziari
Applichiamo adesso il nostro modello di random walk ad alcuni dati finanziari reali. Usiamo le librerie pandas e yfinance di Python per ottenere e gestire facilmente i dati finanziari da Yahoo Finance.
Verifichiamo se un modello di passeggiata aleatoria descrive bene alcuni dati azionari. In particolare, scegliamo Microsoft (MSFT), ma puoi provare anche con il tuo ticker preferito! In questo modo esploriamo meglio il legame tra white noise e random walks.
Prima di scaricare qualsiasi dato, installiamo il pacchetto yfinance perché non fa parte dell’installazione standard di Pandas. Basta eseguire il comando seguente:
pip install yfinance
E’ quindi possibile scaricare i dati di MSFT con una semplice chiamata ad una funzione di pandas-datareader
import datetime
import yfinance as yf
symbol = 'MSFT'
start_date = datetime.datetime(2000, 1, 1)
end_date = datetime.datetime(2017, 1, 8)
mstf = yf.download(
symbol,
start=start_date - datetime.timedelta(days=365),
end=end_date,
group_by='ticker', auto_adjust=False
)
mstf = mstf[symbol]
Creiamo un oggetto chiamato msft dove possiamo accedere alla serie dei prezzi di chiusura aggiustati per lo specifico titolo azionario.
Il nostro processo consiste nel calcolare la differenza dei valori di chiusura, omettere eventuali valori mancanti e quindi applicarli alla funzione di autocorrelazione. Quando tracciamo il correlogramma, cerchiamo prove della presenza di rumore bianco discreto, ovvero una serie di residui non correlata in modo seriale. Per eseguire ciò in Python, eseguiamo il seguente comando:
mstf_close = mstf['Adj Close']
msft_diff = np.diff(mstf_close, n=1)
msft_diff_acf_coef = acf(msft_diff,missing="drop")
plot_acf(msft_diff_acf_coef, lags=20)
plt.show()
L’ultima parte (missing = "drop") specifica alla funzione acf di ignorare i valori NaN. L’output della funzione acf è il seguente:
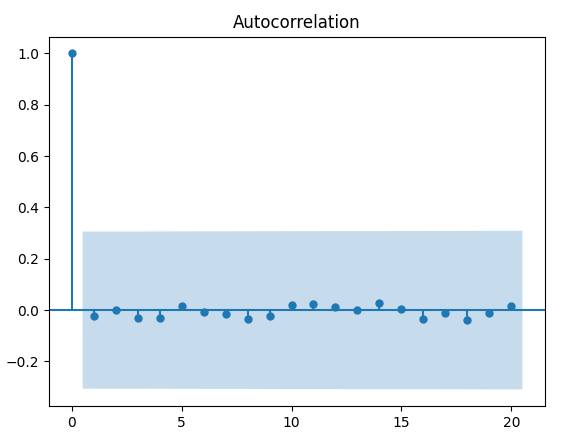
Notiamo che la maggior parte dei picchi di lag non differisce dallo zero per più del 5%. Tuttavia ce ne sono alcuni che sono marginalmente superiori. Dato che i ritardi \( k_i \) per i quali si verifica un picco anomalo sono indipendenti da \( k = 0 \), potremmo essere inclini a pensare che questi siano causati da variazioni stocastiche e non rappresentino alcuna correlazione seriale presente nella serie.
Quindi possiamo concludere, con un ragionevole grado di certezza, che i prezzi di chiusura rettificati di MSFT sono ben approssimati da una random walk.
Modello per l’indice S&P500
Proviamo ora lo stesso approccio sullo stesso indice S&P500. Il simbolo Yahoo Finance per l’S&P500 è ^GSPC. Quindi, se inseriamo i seguenti comandi in Python, possiamo tracciare il correlogramma della serie di differenze dell’S & P500:
symbol = '^GSPC'
sp500 = yf.download(
symbol,
start=start_date - datetime.timedelta(days=365),
end=end_date,
group_by='ticker', auto_adjust=False
)
sp500 = sp500[symbol]
sp500_close = sp500['Adj Close']
sp500_diff = np.diff(sp500_close, n=1)
sp500_diff_acf_coef = acf(sp500_diff,missing="drop")
plot_acf(sp500_diff_acf_coef, lags=20)
plt.show()
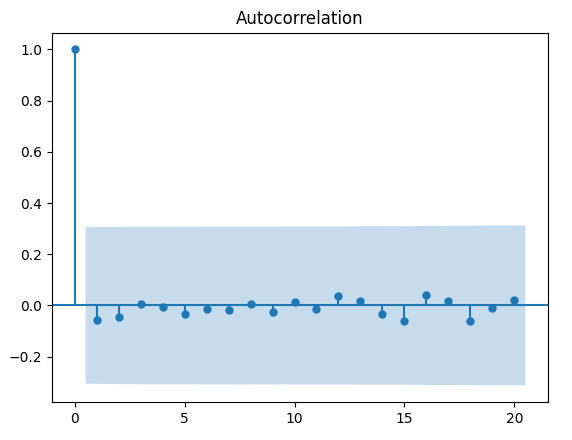
Troviamo questo correlogramma decisamente più interessante. Notiamo una correlazione negativa per \( k = 1 \), che difficilmente attribuiamo alla semplice variazione casuale del campionamento.
Osserviamo anche alcuni picchi per \( k = 1 \), \( k = 15 \) e \( k = 18 \). Sebbene risulti complesso giustificarne la presenza al di là della variazione casuale, possiamo considerarli potenzialmente indicativi di un processo con un ritardo più lungo.
Conclusioni
Alla luce di queste osservazioni, fatichiamo a considerare la random walk un modello adeguato per descrivere l’andamento dei prezzi di chiusura aggiustati dell’S&P500. Il comportamento della serie suggerisce deviazioni significative dal white noise e random walks, indicando strutture interne più complesse e possibili dipendenze temporali non trascurabili.
Per affrontare questa complessità, scegliamo di adottare modelli più sofisticati, in particolare i modelli autoregressivi di ordine p, che ci permettono di catturare le relazioni dinamiche tra i valori passati della serie. Nella prossima lezione esploreremo proprio questi modelli, analizzando come costruirli, stimarli e interpretarli per applicazioni nel trading quantitativo.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“