In questa lezione introduciamo uno dei problemi più importanti e delicati del machine learning: la selezione del modello e il compromesso Bias-Varianza. Affrontiamo una delle sfide più rilevanti nella costruzione di strategie di trading redditizie basate sul machine learning.
La selezione del modello descrive la nostra capacità di valutare le prestazioni di diversi modelli di machine learning per scegliere quello più adatto.
Il compromesso Bias-Varianza rappresenta una caratteristica intrinseca di tutti i modelli supervisionati. Questo compromesso ci impone di bilanciare la flessibilità del modello con la sua capacità di comportarsi correttamente su dati mai osservati (out of sample), ovvero la prestazione di generalizzazione dei modelli.
Introduzione
Iniziamo descrivendo l’importanza della selezione del modello, quindi analizziamo in modo qualitativo il compromesso Bias-Varianza. Infine, concludiamo la lezione derivandone l’espressione matematica e discutiamo le strategie per ridurre i problemi associati.
In questa lezione consideriamo modelli di regressione supervisionati. Li addestriamo su un set di dati etichettati per ottenere una risposta quantitativa. Ad esempio, potremmo voler prevedere i prezzi futuri delle azioni in base a fattori come i prezzi passati, i tassi di interesse o i tassi di cambio.
Rispetto a un modello categoriale o binario, come nella classificazione supervisionata, i modelli di regressione si differenziano per tipo di risposta. Un esempio di classificazione è l’assegnazione di un argomento a un documento testuale da un insieme finito di categorie. Il compromesso Bias-Varianza e la selezione del modello nella classificazione seguono logiche molto simili, con alcune variazioni dovute ai criteri di valutazione. Tratteremo queste differenze in un’ultima lezione.
Nota: per approfondire la notazione del modello che utilizziamo in questa lezione, consigliamo la lettura della lezione sulle basi del machine learning statistico.
Modelli di machine learning
Come in molte nostre analisi sul machine learning, utilizziamo il seguente modello base:
\(\begin{eqnarray} Y = f (X) + \epsilon \end{eqnarray}\)
Questa formula ci dice che il vettore di risposta, \(Y\), dipende da una funzione (potenzialmente non lineare), \(f\), del vettore predittore, \(X\), e da un insieme di errori distribuiti normalmente con media 0 e deviazione standard 1.
Cosa significa tutto questo in pratica?
Ad esempio, il vettore \(X\) può contenere prezzi finanziari ritardati, tassi di interesse, prezzi di derivati o immobili, frequenze di parole in un testo o qualsiasi altro fattore utile a effettuare una previsione.
Il vettore \(Y\) può avere un solo valore (ad esempio il prezzo di domani) o essere multivalore (come le previsioni per i prossimi sette giorni).
La funzione \(f\) rappresenta la relazione tra \(X\) e \(Y\). Se è lineare, la stimiamo con un modello lineare; se è non lineare, possiamo usare una Support Vector Machine o un metodo con spline.
Gli errori \(\epsilon\) comprendono tutti i fattori che influenzano \(Y\) e che la funzione \(f\) non spiega. Rappresentano la componente “sconosciuta” della previsione. Solitamente assumiamo che abbiano distribuzione normale con media 0 e deviazione standard 1.
Misurare le prestazioni
In questa lezione spieghiamo come misurare le prestazioni di una stima per la funzione ignota \(f\), indicata con la notazione “hat”: \(\hat {f} \) significa “stima di \(f\)”.
Descriviamo anche come la flessibilità del modello influisce sulle sue prestazioni. Con flessibilità intendiamo la capacità di aumentare i gradi di libertà per adattarsi meglio ai dati di training. Noteremo che la relazione tra flessibilità ed errore non è lineare, e quindi scegliamo il modello migliore con molta attenzione.
Ricordiamo che nessun modello risulta sempre il migliore per ogni problema di statistica o machine learning. Ogni modello ha punti di forza e limiti. Uno può funzionare bene con un certo set di dati ma male con un altro. La nostra sfida nel machine learning statistico consiste nello scegliere il modello più adatto in base ai dati disponibili e, soprattutto, nel comprendere bene il compromesso Bias-Varianza.
Selezione del modello
Quando cerchiamo il metodo di machine learning statistico più adatto, abbiamo bisogno di strumenti per valutare le prestazioni dei diversi modelli.
Per farlo, confrontiamo i valori noti della relazione sottostante con quelli previsti da un modello stimato.
Ad esempio, se vogliamo prevedere i prezzi delle azioni di domani, valutiamo quanto le previsioni dei nostri modelli si avvicinano al valore reale in una determinata giornata.
Funzione di perdita
Questo ci porta a introdurre il concetto di funzione di perdita, che misura quantitativamente la differenza tra i valori reali e quelli previsti.
Supponiamo di stimare la relazione sottostante \(f\) con \(\hat{f}\). \(\hat{f}\) può rappresentare, ad esempio, una regressione lineare o un modello random forest. Alleniamo \(\hat{f}\) su un set di dati specifico \(\tau\), contenente coppie predittore-risposta. Se il numero di coppie è \(N\), allora \(\tau\) risulta:
\(\begin{eqnarray} \tau = \{(X_1, Y_1), …, (X_N, Y_N) \} \end{eqnarray}\)
I valori \(X_i\) rappresentano i fattori di previsione, come i prezzi ritardati o altri indicatori. I valori \(Y_i\) corrispondono alle previsioni sui prezzi futuri. In questo contesto, \(N\) indica il numero di giorni disponibili nei dati.
Indichiamo la funzione di perdita con \(L(Y, \hat{f}(X))\), e la usiamo per confrontare le previsioni fatte da \(\hat{f}\) con i veri valori \(Y\). Una scelta comune è l’errore assoluto:
\(\begin{eqnarray} L (Y, \hat{f} (X)) = | Y – \hat{f} (X) | \end{eqnarray}\)
Un’alternativa molto usata è l’errore quadratico:
\(\begin{eqnarray} L (Y, \hat{f} (X)) = (Y – \hat{f} (X)) ^2 \end{eqnarray}\)
Entrambe le funzioni di perdita restituiscono sempre valori non negativi. Il valore ottimale di perdita è zero, segnalando l’assenza di differenze tra previsione e valore reale.
Errore di addestramento contro errore di prova
Ora che abbiamo definito una funzione di perdita, vogliamo aggregare le differenze tra valori veri e previsti. Usiamo quindi l’Errore Quadratico Medio (MSE), ovvero la media della perdita al quadrato:
\(\begin{eqnarray} MSE: = \frac {1} {N} \sum ^ {N} _ {i = 1} (Y_i – \hat {f} (X_i)) ^ 2 \end{eqnarray}\)
Questa formula ci dice che il MSE misura la media delle differenze al quadrato tra valori veri \(Y_i\) e valori previsti \(\hat{f}(X_i)\). Più il MSE è basso, più accurata risulta la stima.
Calcoliamo questo MSE sui dati di addestramento, cioè quelli usati per costruire il modello. Per questo motivo, chiamiamo questo valore MSE di training.
Nella pratica, ci interessa poco il MSE di training. Vogliamo sapere quanto bene il modello riesce a prevedere i valori corretti su dati mai visti prima.
Ad esempio, non ci interessa se il modello ha previsto bene i prezzi nel passato; ci interessa capire se riuscirà a prevedere correttamente i prezzi nel futuro. Questa capacità prende il nome di prestazioni di generalizzazione, ed è ciò che conta davvero per noi.
Prestazioni di generalizzazione
Dal punto di vista matematico, se abbiamo un nuovo predittore \(X_0\) e una vera risposta \(Y_0\), allora possiamo calcolare l’MSE di test come:
\(\begin{eqnarray} \text {Test MSE}: = \mathbb {E} \left [(Y_0 – \hat{f} (X_0)) ^2 \right] \end{eqnarray}\)
Qui calcoliamo l’aspettativa su tutte le nuove coppie predittore-risposta \((X_0, Y_0)\) non ancora osservate.
Vogliamo quindi selezionare il modello che presenta il test MSE più basso tra tutte le alternative.
Purtroppo, calcolare il test MSE risulta complicato! Spesso non disponiamo di dati di test.
In ambito machine learning questa situazione è piuttosto comune. Nel trading quantitativo, per fortuna, abbiamo spesso a disposizione grandi quantità di dati. Così possiamo dividere il dataset in una parte per l’addestramento e una per i test. In una prossima lezione, approfondiremo la convalida incrociata, un metodo che ci consente di stimare il test MSE utilizzando sottogruppi dei dati di addestramento.
A questo punto, una domanda interessante è: “Perché non scegliamo semplicemente il modello con il MSE di training più basso?”.
La risposta sta nel fatto che questo approccio non garantisce il miglior test MSE. Il motivo? Entra in gioco una proprietà fondamentale del machine learning statistico, chiamata il compromesso Bias-Varianza.
Comprendere il compromesso Bias-Varianza ci aiuta a trovare il giusto equilibrio tra accuratezza e capacità del modello di generalizzare a dati nuovi.
Il compromesso bias-varianza
Per comprendere il compromesso bias-varianza, immaginiamo una situazione leggermente artificiale in cui conosciamo la vera relazione tra \(Y\) e \(X\). Supponiamo che questa relazione segua una funzione sinusoidale, \(f = \sin\), quindi \(Y = f (X ) = \sin (X)\). Naturalmente, nella pratica non conosciamo mai la funzione sottostante \(f\), ed è proprio per questo che iniziamo stimandola!
In questo scenario artificiale generiamo una serie di punti di allenamento, \(\tau\), secondo l’equazione \(Y_i = \sin (X_i) + \epsilon_i\), dove \(\epsilon_i\) segue una distribuzione normale standard (media zero, deviazione standard uno). La Figura 1 mostra il risultato: la curva nera rappresenta la funzione “vera” \(f\), limitata all’intervallo \([0, 2 \pi]\), mentre i punti cerchiati mostrano i valori dei dati simulati \(Y_i\).
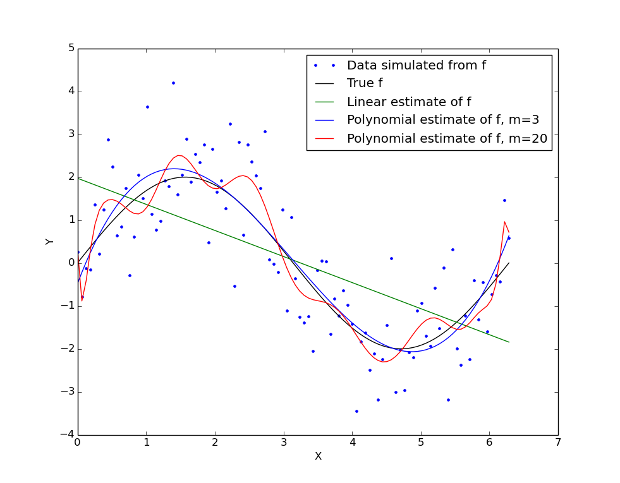
Ora possiamo provare ad adattare alcuni diversi modelli a questi dati di addestramento. Il primo modello, dato dalla linea verde, è una regressione lineare dotata di stima dei minimi quadrati ordinari. Il secondo modello, dato dalla linea blu, è un modello polinomiale con grado \(m = 3\). Il terzo modello, dato dalla curva rossa, è un polinomio di grado superiore con grado \(m = 20\). Tra ciascuno dei modelli abbiamo variato la flessibilità , cioè i gradi di libertà (DoF). Il modello lineare è il meno flessibile con solo due DoF. Il modello più flessibile è il polinomio di ordine \(m = 20\). Si può vedere che il polinomio di ordine \(m = 3\) è l’apparente più vicino adattamento alla relazione sinusoidale sottostante.
Per ciascuno di questi modelli possiamo calcolare il training MSE . Si può vedere nella Figura 2 che il training MSE (dato dalla curva verde) diminuisce monotonicamente all’aumentare della flessibilità del modello. Ciò ha senso, poiché l’adattamento polinomiale può diventare flessibile quanto necessario per ridurre al minimo la differenza tra i suoi valori e quelli dei dati sinusoidali.
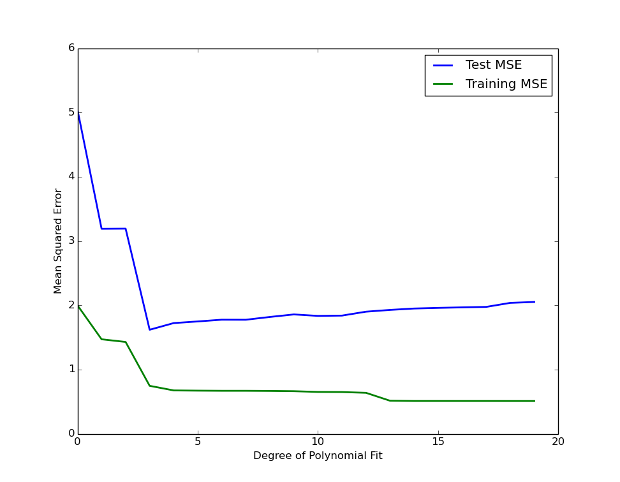
Quando introduciamo nuovi dati nel set di test, il modello fatica a generalizzare. Quei “modelli” che sembravano utili si rivelano essere semplici artefatti casuali nei dati di addestramento, privi di reale significato. In questo scenario entriamo in una situazione di overfitting.
Questa forma “a U” del test MSE rispetto alla flessibilità del modello rappresenta un comportamento tipico nei modelli statistici di machine learning. Si tratta del compromesso bias-varianza, un principio centrale nella valutazione della performance predittiva.
Possiamo dimostrare (come vedremo nella sezione Spiegazione matematica) che il test MSE previsto, calcolato mediando su molti set di addestramento, segue la formula:
\(\begin{eqnarray} \mathbb{E}(Y_0 – \hat{f}(X_0))^2 = \text{Var}(\hat{f}(X_0)) + \left[ \text{Bias} \hat{f}(X_0)\right]^2 + \text{Var}(\epsilon) \end{eqnarray}\)
Analizziamo i tre componenti dell’errore di previsione
Il primo termine rappresenta la varianza della stima su diversi set di addestramento. Quando questa varianza è alta, significa che il nostro modello cambia molto a seconda dei dati usati, eccessivamente adattato ai dati di allenamento.
Il secondo termine è il bias al quadrato, che misura la differenza tra la media delle previsioni e i valori reali. Se il bias è elevato, il modello non coglie il comportamento reale del fenomeno da modellare. Ad esempio, una regressione lineare non riesce a rappresentare una curva sinusoidale, anche se si adatta bene ai dati.
Il terzo termine è l’errore irriducibile, il limite minimo dell’MSE. Dato che lavoriamo con dati osservati e casualità (cioè i termini \(\epsilon\)), non possiamo mai superare questo limite in precisione.
Quando aumentiamo la flessibilità del modello, in genere vediamo un aumento della varianza e una riduzione del bias. Tuttavia, è proprio il compromesso bias-varianza a determinare se l’MSE atteso migliora o peggiora, in base al bilanciamento tra questi due fattori.
All’inizio, l’aumento della flessibilità fa calare rapidamente il bias, mentre la varianza cresce lentamente. In questa fase, il test MSE diminuisce. Poi, aumentando ulteriormente la flessibilità, il bias smette di calare in modo significativo, mentre la varianza cresce rapidamente a causa del sovradimensionamento del modello.
Il nostro obiettivo nel machine learning è ridurre al minimo il test MSE previsto, scegliendo un modello che mantenga sia la bassa varianza sia il basso bias.
Per stimare il test MSE previsto, possiamo utilizzare tecniche come la convalida incrociata, che approfondiremo in una futura lezione.
Per approfondire il compromesso bias-varianza in modo matematico, possiamo consultare la sezione seguente.
Spiegazione matematica
Abbiamo finora delineato qualitativamente i problemi che circondano la flessibilità, il bias e la varianza del modello. Nel seguente riquadro eseguiremo una scomposizione matematica dell’errore di previsione atteso per una particolare stima del modello, \(\hat {f} (X) \) con il vettore di previsione \( X = x_0 \) utilizzando l’ultima delle nostre funzioni di perdita, la perdita di errore al quadrato:La definizione della perdita dell’errore quadratico, nel punto di previsione \(X_0\) $, è data da: \(\begin{eqnarray} \text{Err} (X_0) = \mathbb{E} \left[ \left( Y – \hat{f}(X_0) \right)^2 | X = X_0 \right] \end{eqnarray}\) Tuttavia, possiamo espandere l’aspettativa sul lato destro in tre termini: \(\begin{eqnarray} \text{Err} (X_0) = \sigma^{2}_{\epsilon} + \left[ \mathbb{E} \hat{f} (X_0) – f(X_0)\right]^2 + \mathbb{E} \left[ \hat{f}(X_0) – \mathbb{E} \hat{f}(X_0) \right]^2 \end{eqnarray}\) Il primo termine sulla RHS è noto come errore irriducibile . È il limite inferiore del possibile errore di previsione. Il termine medio è il bias al quadrato e rappresenta la differenza tra valore medio di tutte le previsioni a \(X_0\), in tutti i possibili set di addestramento, e il vero valore medio della funzione sottostante a \(X_0\). Questo può essere visto come l’errore introdotto dal modello nel non rappresentare il comportamento base della vera funzione. Ad esempio, utilizzando un modello lineare quando il fenomeno è intrinsecamente non lineare. Il terzo termine è noto come varianza . Caratterizza l’errore introdotto quando il modello diventa più flessibile e quindi più sensibile alle variazioni tra diversi set di addestramento, \(\tau\). \(\begin{eqnarray} \text{Err} (X_0) &=& \sigma^{2}_{\epsilon} + \text{Bias}^2 + \text{Var} (\hat{f}(X_0))\\ &=& \text{Irreducible Error} + \text{Bias}^2 + \text{Variance} \end{eqnarray}\) È importante ricordare che \(\sigma^{2} _ \epsilon\) rappresenta un limite inferiore assoluto dell’errore di previsione. Mentre l’errore di addestramento atteso può essere ridotto monotonicamente a zero (semplicemente aumentando la flessibilità del modello), l’errore di previsione atteso sarà sempre almeno l’errore irriducibile, anche se il bias al quadrato e la varianza sono entrambi zero.

