Quando sviluppiamo strategie predittive per il trading quantitativo, affrontiamo spesso il problema dell’ottimizzazione e del rischio di overfitting. La cross-validation nel machine learning rappresenta uno strumento essenziale per ridurre l’errore di generalizzazione e valutare correttamente le prestazioni fuori campione dei modelli statistici. In questa lezione ci concentriamo proprio su come utilizzare la cross-validation nel machine learning per aumentare l’affidabilità delle previsioni.
Sappiamo bene quanto sia facile ottenere risultati eccellenti durante un backtest, ma questi possono trarci in inganno se il modello si adatta eccessivamente ai dati storici. In questo caso rischiamo di generare una strategia con prestazioni illusorie, che delude una volta applicata al mercato reale.
Per questo motivo, esploriamo ora in dettaglio la cross-validation nel machine learning, con l’obiettivo di migliorare le nostre strategie predittive e ridurre l’overfitting. Utilizzeremo esempi pratici basati su dati di mercato, accompagnati da codice in Python, per rendere applicabili i concetti trattati.
In questa lezione introduciamo il concetto di cross-validation e ne analizziamo il funzionamento. In seguito costruiamo un modello predittivo basato su un indice azionario e applichiamo due metodi: il validation set approach e la k-fold cross-validation. Infine, discutiamo l’implementazione pratica in Python utilizzando Pandas, Matplotlib e Scikit-Learn.
Questa lezione si collega idealmente a quanto trattato nel nostro precedente contributo sul compromesso bias-varianza. In quel contesto abbiamo menzionato la cross-validation come metodo efficace per affrontare i problemi legati al trade-off tra bias e varianza.
Il nostro scopo è sviluppare strumenti statistici da integrare nei motori di backtesting, così da contenere il rischio di overfitting e ridurre le perdite causate da modelli troppo ottimizzati.
Panoramica della Cross-Validation
Nel nostro precedente approfondimento sul compromesso bias-varianza abbiamo introdotto due concetti fondamentali:
- Errore di test: la media dell’errore predittivo di un modello calcolata su nuove osservazioni non utilizzate in fase di addestramento.
- Flessibilità: il numero di gradi di libertà che un modello possiede per adattarsi ai dati. Ad esempio, una regressione lineare è molto rigida, mentre un modello polinomiale ad alto grado risulta estremamente flessibile.
Con queste nozioni ben presenti, definiamo la cross-validation:
La cross-validation serve a stimare l’errore di test di un modello statistico oppure a scegliere il livello di flessibilità più adatto al metodo impiegato.
Ricordiamo ancora una volta come l’errore di addestramento sottovaluti l’errore di test. La cross-validation ci consente di ottenere una stima più accurata di quest’ultimo, fondamentale quando ci manca una base di verità nota.
Per eseguire la cross-validation nel machine learning, dividiamo il dataset in sottoinsiemi: ne usiamo alcuni per l’addestramento e altri per il test. In questa lezione illustriamo le modalità di suddivisione e applichiamo i metodi su un modello predittivo costruito su dati di mercato.
Esempio di previsione
Per rendere più concreto il contenuto, sviluppiamo una strategia di trading basata sulla previsione dei livelli di prezzo di un indice azionario. Scegliamo l’indice S&P500, che rappresenta le cinquecento maggiori aziende quotate negli Stati Uniti. Potremmo applicare la stessa logica anche all’Euro Stoxx 50 o al DAX.
Per questa strategia consideriamo i prezzi OHLC giornalieri come predittori e il prezzo di chiusura del giorno successivo come risposta. In sostanza, tentiamo di prevedere il prezzo di domani a partire dai dati storici.
Ogni osservazione è costituita da una coppia di vettori, \(X\) e \(y\), dove \(X\) contiene i predittori (i prezzi di chiusura dei giorni precedenti) e \(y\) il prezzo di chiusura di domani. Se scegliamo un ritardo di \(p\) giorni, \(X\) ha \(p\) componenti, e ogni componente rappresenta il prezzo di chiusura di un giorno.
Il vettore \(Y\) include un solo valore scalare: il prezzo di chiusura del giorno successivo. L’intero dataset si compone di \(n\) osservazioni, che coprono \(n\) giorni di dati storici del S&P500.
Il nostro obiettivo consiste nel costruire un modello statistico capace di prevedere il prezzo del giorno successivo usando le chiusure precedenti. Se raggiungiamo una buona precisione, possiamo derivare segnali di trading dalla previsione. In questa lezione ci focalizziamo sul lato predittivo, lasciando da parte l’esecuzione operativa.
Usiamo la cross-validation nel machine learning in due modi: da un lato per stimare le prestazioni predittive di ciascun metodo statistico, dall’altro per ottimizzare il livello di flessibilità del modello riducendo bias e varianza.
Descriviamo infine due tecniche principali di validazione incrociata: l’approccio dell’insieme di convalida e la k-fold cross-validation. Per implementare questi metodi utilizziamo Pandas e Scikit-Learn.
Validation Set Approach
Nella cross-validation nel machine learning, l’approccio del set di convalida risulta semplice da applicare. Dividiamo l’insieme delle osservazioni (\(n\) giorni di dati) in due metà scelte casualmente. Una metà diventa il set di addestramento, l’altra il set di convalida. Alleniamo il modello solo con il set di addestramento e stimiamo l’errore di test utilizzando esclusivamente il set di convalida.
Utilizziamo spesso questa tecnica nel trading quantitativo per valutare la capacità predittiva dei modelli. Più comunemente, scegliamo due terzi dei dati per l’addestramento e il terzo rimanente per la convalida. In genere, rispettiamo l’ordine cronologico dei dati, assegnando i primi due terzi del periodo al set di addestramento.
Di rado mescoliamo casualmente le osservazioni nei due set. Ancora più raramente affrontiamo i problemi sottili che emergono dalla randomizzazione.
Soprattutto quando disponiamo di pochi dati, rischiamo di ottenere una varianza elevata nella stima dell’errore di test a causa della casualità nella suddivisione. Nella cross-validation nel machine learning, questa situazione rappresenta una trappola comune. Se dividiamo il campione in modo fortunato, rischiamo di stimare un errore di test troppo basso, sottovalutando il reale potere predittivo del modello.
Inoltre, nella suddivisione 50-50 tra addestramento e test, escludiamo metà delle osservazioni. Di conseguenza, riduciamo le informazioni a disposizione per l’addestramento e compromettiamo la qualità del modello. In questo modo, rischiamo di sovrastimare l’errore di test sull’intero dataset.
Per affrontare queste limitazioni, consideriamo una strategia più evoluta: la convalida incrociata k-fold.
k-Fold Cross-Validation nel Machine Learning
Con la convalida incrociata k-fold, miglioriamo l’approccio a set di convalida suddividendo le \(n\) osservazioni in \(k\) sottoinsiemi mutuamente esclusivi, detti “fold”, di dimensioni simili.
Utilizziamo il primo fold come set di convalida e i rimanenti \(k-1\) come set di addestramento. Alleniamo il modello e stimiamo l’errore di test sul fold di convalida. Ripetiamo questo processo \(k\) volte, usando ogni fold una volta come set di convalida e aggregando gli altri \(k-1\) per l’addestramento.
Otteniamo così una stima globale dell’errore di test, \(\text{CV}_k\), calcolata come media degli errori quadratici medi \(\text{MSE}_i\) di ogni fold:
\(\begin{eqnarray} \text {CV} _k = \frac {1} {k} \sum ^ {k} _ {i = 1} \text {MSE} _i \end{eqnarray}\)
A questo punto ci chiediamo come scegliere il valore di \(k\)? Secondo l’esperienza empirica, \(k = 5\) o \(k = 10\) risultano scelte efficaci. Tuttavia, la decisione dipende anche dalla complessità computazionale e dal compromesso tra bias e varianza, aspetti centrali nella cross-validation nel machine learning.
Leave-One-Out Cross Validation
Possiamo anche scegliere \(k = n\), adattando il modello \(n\) volte, escludendo una sola osservazione per volta. Chiamiamo questa tecnica validazione incrociata leave-one-out (LOOCV). Questa scelta, però, comporta costi computazionali elevati se \(n\) è grande e il modello richiede molto per adattarsi.
LOOCV riduce il bias, dato che usiamo quasi tutti i dati per l’addestramento, ma introduce una varianza elevata. Questo accade perché stimiamo l’errore di test su una singola risposta alla volta.
La convalida incrociata k-fold riduce questa varianza, introducendo però un piccolo incremento del bias, visto che non utilizziamo ogni osservazione in ogni fase. Con \(k = 5\) o \(k = 10\), il bilanciamento tra bias e varianza risulta generalmente ottimale nella pratica della cross-validation nel machine learning.
Implementazione in Python
Quando lavoriamo con Python e il suo ricco ecosistema di librerie, ci sentiamo fortunati: possiamo evitare gran parte del “lavoro pesante” e risparmiamo tempo ed energie! Con l’aiuto di Pandas, Scikit-Learn e Matplotlib, costruiamo rapidamente esempi per illustrare l’utilizzo pratico e le sfide legate alla cross-validation nel machine learning.
Se non abbiamo ancora configurato un ambiente Python per la ricerca, consigliamo vivamente di scaricare il pacchetto Anaconda di Continuum Analytics, che include tutte le librerie necessarie per questa lezione e un IDE pronto all’uso chiamato Spyder.
Ottenere i dati
Per prima cosa, otteniamo i dati e li convertiamo in un formato adatto all’analisi. Possiamo usare il codice seguente per scaricare dati storici da qualsiasi serie temporale finanziaria disponibile su Yahoo Finanza e calcolare i ritardi predittivi giornalieri associati.
import datetime
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
def create_lagged_series(symbol, start_date, end_date, lags=5):
"""
Si crea un DataFrame pandas che memorizza i rendimenti percentuali dei
prezzi di chiusura rettificata di un titolo azionario ottenuta da Yahoo
Finance, insieme a una serie di rendimenti ritardati dai giorni di negoziazione
precedenti (i valori predefiniti ritardano di 5 giorni).
Sono inclusi anche il volume degli scambi, così come la direzione del giorno precedente.
"""
# Ottieni informazioni sulle azioni da Yahoo Finance
ts = yf.download(
symbol,
start=start_date - datetime.timedelta(days=365),
end=end_date,
group_by='ticker', auto_adjust=False
)
ts = ts[symbol]
# Crea un nuovo Dataframe per i ritardi
tslag = pd.DataFrame(index=ts.index)
tslag["Today"] = ts["Adj Close"]
tslag["Volume"] = ts["Volume"]
# Crea la serie traslata dei ritardi dei prezzi di chiusura del periodo (giorno) precedente
for i in range(0,lags):
tslag["Lag%s" % str(i+1)] = ts["Adj Close"].shift(i+1)
# Crea il DataFrame dei ritorni
tsret = pd.DataFrame(index=tslag.index)
tsret["Volume"] = tslag["Volume"]
tsret["Today"] = tslag["Today"].pct_change()*100.0
# Se uno qualsiasi dei valori dei ritorni percentuali è uguale a zero, si impostano
# a un numero piccolo (per non avere problemi con il modello QDA in scikit-learn)
for i,x in enumerate(tsret["Today"]):
if (abs(x) < 0.0001):
tsret["Today"][i] = 0.0001
# Crea la serie dei ritorni precedenti percentuali
for i in range(0,lags):
tsret["Lag%s" % str(i+1)] = tslag["Lag%s" % str(i+1)].pct_change()*100.0
# Crea la serie "Direction" (+1 o -1) che indica un giorno up/down
tsret["Direction"] = np.sign(tsret["Today"])
tsret = tsret[tsret.index >= start_date]
return tsret
Il codice memorizza i valori del prezzo di chiusura direttamente nelle colonne “Today” o “Lags”. Inoltre, calcola e memorizza il rendimento percentuale tra i prezzi di chiusura di un giorno e del giorno precedente.
Dobbiamo ottenere i dati per i prezzi giornalieri del SP500 per un periodo di tempo adeguato. Consideriamo uno storico dal 1 ° gennaio 2004 al 31 dicembre 2004. Questa è una scelta arbitraria. Possiamo configurare l’intervallo di tempo che desideriamo. Per ottenere i dati e inserirli in un Pandas DataFrame chiamato sp500_lags possiamo utilizzare il seguente codice:
if __name__ == "__main__":
symbol = "^GSPC"
start_date = datetime.datetime(2004, 1, 1)
end_date = datetime.datetime(2004, 12, 31)
sp500_lags = create_lagged_series(symbol, start_date, end_date, lags=5)
A questo punto disponiamo dei dati necessari per iniziare a costruire una serie di modelli statistici di machine learning.
Validation Set Approach
Ora che disponiamo dei dati finanziari necessari per creare una serie di modelli di regressione predittiva, possiamo applicare i metodi di convalida incrociata descritti sopra per stimare l’errore di test.
Iniziamo importando i modelli da Scikit-Learn. Scegliamo un modello di regressione lineare con caratteristiche polinomiali, così possiamo variare la flessibilità modificando il grado dell’ordine polinomiale delle feature. Iniziamo adottando l’approccio del set di convalida per la cross-validation nel machine learning.
Scikit-Learn include un metodo per il validation set, train_test_split, che troviamo nel modulo cross_validation. Importiamo anche il metodo KFold per la convalida incrociata k-fold, insieme al modello di regressione lineare. Includiamo il calcolo dell’MSE, oltre a Pipeline e PolynomialFeatures. Questi ultimi ci permettono di costruire rapidamente una serie di modelli di regressione lineare con feature polinomiali, scrivendo pochissimo codice aggiuntivo.
..
from sklearn.model_selection import train_test_split, KFold
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
..
Una volta importati i moduli, possiamo creare un DataFrame SP500 che utilizza i rendimenti in ritardo dei cinque giorni precedenti come predittori. Possiamo quindi creare dieci separate suddivisioni casuali dei dati in un set di addestramento e convalida.
Infine, per gradi multipli delle features polinomiali della regressione lineare, possiamo calcolare l’errore di test. Questo ci fornisce dieci separate curve di errore di test, ogni valore delle quali mostra il test MSE per un grado diverso del kernel polinomiale:
..
..
def validation_set_poly(random_seeds, degrees, X, y):
"""
Utilizza il metodo train_test_split per creare un set
di addestramento e un set di convalida (50% per ciascuno)
utilizzando separati campionamenti casuali "random_seeds"
per modelli di regressione lineare di varia flessibilità
"""
sample_dict = dict([("seed_%s" % i,[]) for i in range(1, random_seeds+1)])
# Esegui un ciclo su ogni suddivisione casuale in una suddivisione train-test
for i in range(1, random_seeds+1):
print("Random: %s" % i)
# Aumenta il grado di ordine polinomiale della regressione lineare
for d in range(1, degrees+1):
print("Degree: %s" % d)
# Crea il modello, divide gli insiemi e li addestra
polynomial_features = PolynomialFeatures(
degree=d, include_bias=False
)
linear_regression = LinearRegression()
model = Pipeline([
("polynomial_features", polynomial_features),
("linear_regression", linear_regression)
])
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, random_state=i
)
model.fit(X_train, y_train)
# Calcola il test MSE e lo aggiunge al
# dizionario di tutte le curve di test
y_pred = model.predict(X_test)
test_mse = mean_squared_error(y_test, y_pred)
sample_dict["seed_%s" % i].append(test_mse)
# Converte queste liste in array numpy per calcolare la media
sample_dict["seed_%s" % i] = np.array(sample_dict["seed_%s" % i])
# Crea la serie delle "medie dei test MSE" colcolando la media
# del test MSE per ogni grado dei modelli di regressione lineare,
# attraverso tutti i campionamenti casuali
sample_dict["avg"] = np.zeros(degrees)
for i in range(1, random_seeds+1):
sample_dict["avg"] += sample_dict["seed_%s" % i]
sample_dict["avg"] /= float(random_seeds)
return sample_dict
..
..
Possiamo usare Matplotlib per tracciare il grafico di questi dati. Dobbiamo importare pylab e quindi creare una funzione per tracciare le curve di errore di test:
..
..
def plot_test_error_curves_vs(sample_dict, random_seeds, degrees):
fig, ax = plt.subplots()
ds = range(1, degrees+1)
for i in range(1, random_seeds+1):
ax.plot(ds, sample_dict["seed_%s" % i], lw=2, label='Test MSE - Sample %s' % i)
ax.plot(ds, sample_dict["avg"], linestyle='--', color="black", lw=3, label='Avg Test MSE')
ax.legend(loc=0)
ax.set_xlabel('Degree of Polynomial Fit')
ax.set_ylabel('Mean Squared Error')
ax.set_ylim([0.0, 4.0])
fig.set_facecolor('white')
plt.show()
..
..
Abbiamo selezionato il grado delle nostre features polinomiali al variare tra \(d = 1\) e \(d = 3\), prevedendo così un ordine cubico nelle nostre features. La seguente Figura 1 mostra le dieci diverse suddivisioni casuali dei dati di addestramento e test, insieme alla media del test MSE (la linea tratteggiata nera):
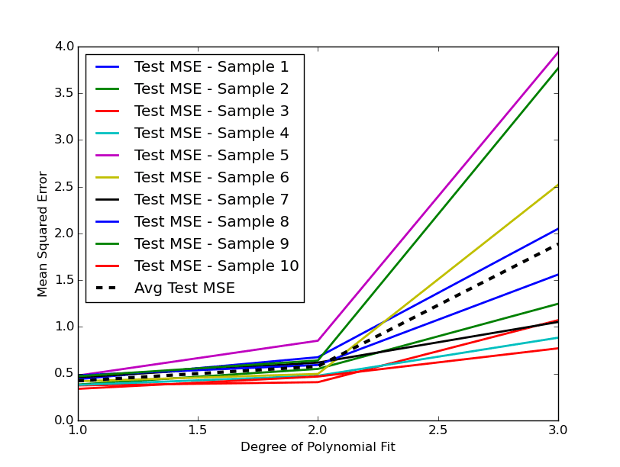
Notiamo subito quanta variazione emerga tra diverse suddivisioni casuali tra il set di addestramento e quello di convalida. Poiché i prezzi di chiusura storici dei giorni precedenti dell’SP500 offrono poco segnale predittivo, osserviamo che, aumentando il grado delle feature polinomiali, il test MSE aumenta.
Inoltre, vediamo chiaramente che il set di convalida presenta un’elevata varianza. Quando utilizziamo il modello con grado \(d = 3\), otteniamo un test MSE medio di circa 1,9 con l’approccio basato sul set di validazione.
Per affrontare questo problema, decidiamo di applicare la convalida incrociata k-fold sullo stesso set di dati dell’SP500. Questa tecnica rappresenta una forma efficace di cross-validation nel machine learning.
k-Fold Cross Validation
Poiché abbiamo già gestito le importazioni necessarie, ora ci concentriamo sulla definizione delle nuove funzioni per eseguire la convalida incrociata k-fold. Queste funzioni assomigliano molto a quelle usate per suddividere il set di addestramento. Tuttavia, ora utilizziamo l’oggetto KFold per iterare su \(k\) “fold”.
In particolare, l’oggetto KFold fornisce un iteratore che ci consente di indicizzare in modo corretto i campioni del dataset e creare fold distinti per training e test. In questo esempio, scegliamo \(k = 10\).
Come già fatto con l’approccio del set di convalida, costruiamo una pipeline che trasforma le feature in polinomi e applichiamo un modello di regressione lineare. Poi calcoliamo il test MSE per ogni fold e tracciamo le curve corrispondenti. Infine, creiamo una curva MSE media tra tutti i fold:
..
..
def k_fold_cross_val_poly(folds, degrees, X, y):
kf = KFold(n_splits=folds, shuffle=False)
kf_dict = dict([("fold_%s" % i,[]) for i in range(1, folds+1)])
fold = 0
for train_index, test_index in kf.split(X):
fold += 1
print("Fold: %s" % fold)
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
for d in range(1, degrees+1):
print("Degree: %s" % d)
model = Pipeline([
("polynomial_features", PolynomialFeatures(degree=d, include_bias=False)),
("linear_regression", LinearRegression())
])
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
test_mse = mean_squared_error(y_test, y_pred)
kf_dict["fold_%s" % fold].append(test_mse)
kf_dict["fold_%s" % fold] = np.array(kf_dict["fold_%s" % fold])
kf_dict["avg"] = np.zeros(degrees)
for i in range(1, folds+1):
kf_dict["avg"] += kf_dict["fold_%s" % i]
kf_dict["avg"] /= float(folds)
return kf_dict
..
..
Possiamo tracciare queste curve con la seguente funzione:
..
..
def plot_test_error_curves_kf(kf_dict, folds, degrees):
fig, ax = plt.subplots()
ds = range(1, degrees+1)
for i in range(1, folds+1):
ax.plot(ds, kf_dict["fold_%s" % i], lw=2, label='Test MSE - Fold %s' % i)
ax.plot(ds, kf_dict["avg"], linestyle='--', color="black", lw=3, label='Avg Test MSE')
ax.legend(loc=0)
ax.set_xlabel('Degree of Polynomial Fit')
ax.set_ylabel('Mean Squared Error')
ax.set_ylim([0.0, 4.0])
fig.set_facecolor('white')
plt.show()
..
..
L’output è riportato nella seguente Figura 2:
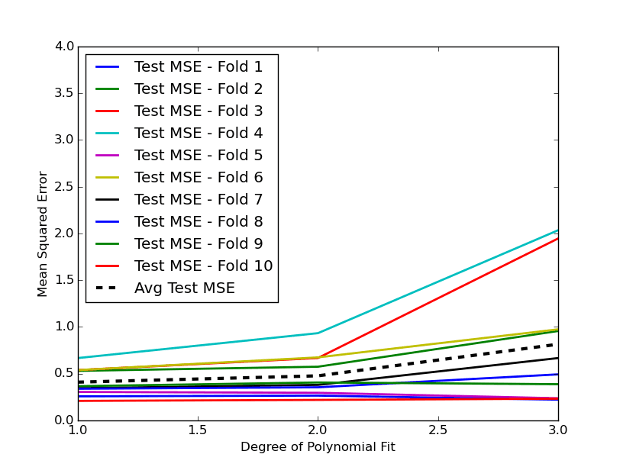
Notiamo che la variazione tra le curve di errore risulta molto più contenuta rispetto all’approccio del validation set. Questo effetto rappresenta proprio l’obiettivo che vogliamo ottenere eseguendo la convalida incrociata. In particolare, per \(d = 3\), otteniamo una riduzione dell’errore medio di test di circa 0,8.
Conclusione
Utilizziamo la cross-validation nel machine learning per stimare con maggiore precisione il vero MSE di test, anche se comporta un leggero bias. Questo compromesso ci appare generalmente accettabile nelle applicazioni pratiche di machine learning.
Nelle prossime lezioni esploreremo approcci alternativi di ricampionamento, come il Bootstrap, il Bootstrap Aggregation (“Bagging”) e il Boosting. Queste tecniche più sofisticate ci permetteranno di selezionare i modelli in modo più efficace e, con un po’ di fortuna, di ridurre ulteriormente i nostri errori.
Codice Python Completo
Di seguito il codice Python completo per il file cross_validation.py:
import datetime
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, KFold
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
def create_lagged_series(symbol, start_date, end_date, lags=5):
"""
Si crea un DataFrame pandas che memorizza i rendimenti percentuali dei
prezzi di chiusura rettificata di un titolo azionario ottenuta da Yahoo
Finance, insieme a una serie di rendimenti ritardati dai giorni di negoziazione
precedenti (i valori predefiniti ritardano di 5 giorni).
Sono inclusi anche il volume degli scambi, così come la direzione del giorno precedente.
"""
# Ottieni informazioni sulle azioni da Yahoo Finance
ts = yf.download(
symbol,
start=start_date - datetime.timedelta(days=365),
end=end_date,
group_by='ticker', auto_adjust=False
)
ts = ts[symbol]
# Crea un nuovo Dataframe per i ritardi
tslag = pd.DataFrame(index=ts.index)
tslag["Today"] = ts["Adj Close"]
tslag["Volume"] = ts["Volume"]
# Crea la serie traslata dei ritardi dei prezzi di chiusura del periodo (giorno) precedente
for i in range(0,lags):
tslag["Lag%s" % str(i+1)] = ts["Adj Close"].shift(i+1)
# Crea il DataFrame dei ritorni
tsret = pd.DataFrame(index=tslag.index)
tsret["Volume"] = tslag["Volume"]
tsret["Today"] = tslag["Today"].pct_change()*100.0
# Se uno qualsiasi dei valori dei ritorni percentuali è uguale a zero, si impostano
# a un numero piccolo (per non avere problemi con il modello QDA in scikit-learn)
for i,x in enumerate(tsret["Today"]):
if (abs(x) < 0.0001):
tsret["Today"][i] = 0.0001
# Crea la serie dei ritorni precedenti percentuali
for i in range(0,lags):
tsret["Lag%s" % str(i+1)] = tslag["Lag%s" % str(i+1)].pct_change()*100.0
# Crea la serie "Direction" (+1 o -1) che indica un giorno up/down
tsret["Direction"] = np.sign(tsret["Today"])
tsret = tsret[tsret.index >= start_date]
return tsret
def validation_set_poly(random_seeds, degrees, X, y):
"""
Utilizza il metodo train_test_split per creare un set
di addestramento e un set di convalida (50% per ciascuno)
utilizzando separati campionamenti casuali "random_seeds"
per modelli di regressione lineare di varia flessibilità
"""
sample_dict = dict([("seed_%s" % i,[]) for i in range(1, random_seeds+1)])
# Esegui un ciclo su ogni suddivisione casuale in una suddivisione train-test
for i in range(1, random_seeds+1):
print("Random: %s" % i)
# Aumenta il grado di ordine polinomiale della regressione lineare
for d in range(1, degrees+1):
print("Degree: %s" % d)
# Crea il modello, divide gli insiemi e li addestra
polynomial_features = PolynomialFeatures(
degree=d, include_bias=False
)
linear_regression = LinearRegression()
model = Pipeline([
("polynomial_features", polynomial_features),
("linear_regression", linear_regression)
])
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, random_state=i
)
model.fit(X_train, y_train)
# Calcola il test MSE e lo aggiunge al
# dizionario di tutte le curve di test
y_pred = model.predict(X_test)
test_mse = mean_squared_error(y_test, y_pred)
sample_dict["seed_%s" % i].append(test_mse)
# Converte queste liste in array numpy per calcolare la media
sample_dict["seed_%s" % i] = np.array(sample_dict["seed_%s" % i])
# Crea la serie delle "medie dei test MSE" colcolando la media
# del test MSE per ogni grado dei modelli di regressione lineare,
# attraverso tutti i campionamenti casuali
sample_dict["avg"] = np.zeros(degrees)
for i in range(1, random_seeds+1):
sample_dict["avg"] += sample_dict["seed_%s" % i]
sample_dict["avg"] /= float(random_seeds)
return sample_dict
def plot_test_error_curves_vs(sample_dict, random_seeds, degrees):
fig, ax = plt.subplots()
ds = range(1, degrees+1)
for i in range(1, random_seeds+1):
ax.plot(ds, sample_dict["seed_%s" % i], lw=2, label='Test MSE - Sample %s' % i)
ax.plot(ds, sample_dict["avg"], linestyle='--', color="black", lw=3, label='Avg Test MSE')
ax.legend(loc=0)
ax.set_xlabel('Degree of Polynomial Fit')
ax.set_ylabel('Mean Squared Error')
ax.set_ylim([0.0, 4.0])
fig.set_facecolor('white')
plt.show()
def k_fold_cross_val_poly(folds, degrees, X, y):
kf = KFold(n_splits=folds, shuffle=False)
kf_dict = dict([("fold_%s" % i,[]) for i in range(1, folds+1)])
fold = 0
for train_index, test_index in kf.split(X):
fold += 1
print("Fold: %s" % fold)
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
for d in range(1, degrees+1):
print("Degree: %s" % d)
model = Pipeline([
("polynomial_features", PolynomialFeatures(degree=d, include_bias=False)),
("linear_regression", LinearRegression())
])
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
test_mse = mean_squared_error(y_test, y_pred)
kf_dict["fold_%s" % fold].append(test_mse)
kf_dict["fold_%s" % fold] = np.array(kf_dict["fold_%s" % fold])
kf_dict["avg"] = np.zeros(degrees)
for i in range(1, folds+1):
kf_dict["avg"] += kf_dict["fold_%s" % i]
kf_dict["avg"] /= float(folds)
return kf_dict
def plot_test_error_curves_kf(kf_dict, folds, degrees):
fig, ax = plt.subplots()
ds = range(1, degrees+1)
for i in range(1, folds+1):
ax.plot(ds, kf_dict["fold_%s" % i], lw=2, label='Test MSE - Fold %s' % i)
ax.plot(ds, kf_dict["avg"], linestyle='--', color="black", lw=3, label='Avg Test MSE')
ax.legend(loc=0)
ax.set_xlabel('Degree of Polynomial Fit')
ax.set_ylabel('Mean Squared Error')
ax.set_ylim([0.0, 4.0])
fig.set_facecolor('white')
plt.show()
if __name__ == "__main__":
symbol = "^GSPC"
start_date = datetime.datetime(2004, 1, 1)
end_date = datetime.datetime(2004, 12, 31)
sp500_lags = create_lagged_series(symbol, start_date, end_date, lags=5)
# Uso tutti e venti i ritorni di 2 giorni precedenti come
# valori di predizione, con "Today" come risposta
X = sp500_lags[[
"Lag1", "Lag2", "Lag3", "Lag4", "Lag5",
# "Lag6", "Lag7", "Lag8", "Lag9", "Lag10",
# "Lag11", "Lag12", "Lag13", "Lag14", "Lag15",
# "Lag16", "Lag17", "Lag18", "Lag19", "Lag20"
]]
y = sp500_lags["Today"]
degrees = 3
# Visualizza le curve dell'errore di test per il set di validazione
random_seeds = 10
sample_dict_val = validation_set_poly(random_seeds, degrees, X, y)
plot_test_error_curves_vs(sample_dict_val, random_seeds, degrees)
# Visualizza le curve dell'errore di test per il set di k-fold CV
folds = 10
kf_dict = k_fold_cross_val_poly(folds, degrees, X, y)
plot_test_error_curves_kf(kf_dict, folds, degrees)
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

