In questa lezione descriviamo una tecnica ben nota, la regressione lineare, inserendola in un contesto matematico più rigoroso e con un’interpretazione probabilistica del machine learning. Grazie a questo approccio, comprendiamo meglio il quadro delle probabilità, che useremo in seguito per modelli di apprendimento supervisionato più avanzati, partendo da uno scenario più semplice. In questo percorso introduciamo anche il metodo della massima verosimiglianza.
Cominciamo definendo la regressione lineare multipla, collocandola in un framework di apprendimento supervisionato probabilistico. Da qui, ricaviamo una stima ottimale dei parametri attraverso una tecnica nota come metodo della massima verosimiglianza.
Nelle lezioni successive esploriamo i metodi per ridurre o limitare la dimensione di alcuni set di dati utilizzando i concetti di selezione e restringimento di sottoinsiemi. Inoltre, utilizziamo la libreria Scikit-Learn di Python per mostrare l’applicazione pratica della regressione lineare, della selezione di sottoinsiemi e del restringimento.
Molte di queste tecniche si applicano facilmente a modelli più complessi e ci supportano nella creazione di metodi statistici robusti ed efficaci per sviluppare strategie di trading.
Questa lezione adotta un approccio molto più rigoroso dal punto di vista matematico rispetto alle precedenti. Lo facciamo per introdurre un meccanismo probabilistico più evoluto, che costituisce la base della ricerca sull’apprendimento automatico. Dopo aver analizzato alcuni modelli semplici all’interno di questo framework, consultiamo con maggiore facilità i documenti accademici più avanzati nel campo del Machine Learning, utili per ottenere nuove idee di trading.
Regressione lineare
Consideriamo la regressione lineare come una delle tecniche statistiche più intuitive e diffuse. La incontriamo già durante il liceo, sebbene in forma semplificata. Spesso rappresenta anche il primo approccio allo studio dell’apprendimento supervisionato, poiché introduce questioni fondamentali comuni a molti altri modelli supervisionati.
Affermiamo che il valore della risposta \(y\) è una funzione lineare delle feature d’ingresso \({\bf x}\), ovvero:
\(\begin{eqnarray}y ({\bf x}) = \beta^T {\bf x} + \epsilon = \sum_{j=0}^p \beta_j x_j + \epsilon\end{eqnarray}\)
Dove \(\beta^T, {\bf x} \in \mathbb{R}^{p+1}\) e \(\epsilon \sim \mathcal{N}(\mu, \sigma^2)\), ossia \(\beta^T\) e \(x\) sono entrambi vettori di dimensione p+1 e \(\epsilon\), l’errore o il residuo, segue una distribuzione normale con media \(\mu\) e varianza \(\sigma^2\). \(\epsilon\) rappresenta la differenza tra le nostre previsioni ottenute con la regressione lineare e il vero valore della variabile di risposta.
Notiamo che \(\beta^T\), la trasposizione del vettore \(\beta\), e \(x\) hanno dimensione p+1 e non p perché includiamo un termine di intercetta. Infatti, definiamo \(\beta^T = (\beta_0, \beta_1, \ldots, \beta_p)\), mentre \({\bf x} = (1, x_1, \ldots, x_p)\). Inseriamo ‘1’ in \(x\) come una notazione utile a semplificare il calcolo.
Interpretazione probabilistica
Descriviamo la regressione lineare anche come un modello di probabilità congiunta. In altre parole, analizziamo la probabilità congiunta della risposta y dato il vettore delle feature x e gli altri parametri del modello (raccolti nel vettore \({\bf \theta}\)). Esprimiamo quindi il modello nella forma \(p(y \mid {\bf x}, {\bf \theta})\), cioè una densità di probabilità condizionata (CPD).
Scriviamo la regressione lineare come CPD nel seguente modo:
\(\begin{eqnarray}p(y \mid {\bf x}, {\bf \theta}) = \mathcal (y \mid \mu({\bf x}), \sigma^2 ({\bf x}))\end{eqnarray}\)
Per la regressione lineare assumiamo che \(\mu({\bf x})\) sia una funzione lineare e scriviamo quindi \(\mu ({\bf x}) = \beta^T {\bf x}\). Stabiliamo anche che la varianza resti fissa (indipendente da x), ottenendo \(\sigma^2 ({\bf x}) = \sigma^2\), una costante. Queste assunzioni ci portano a definire il vettore dei parametri come \(\theta = (\beta, \sigma^2)\).
Abbiamo già utilizzato questa interpretazione probabilistica nella regressione lineare bayesiana, che abbiamo trattato in una lezione precedente.
Estendendo l’interpretazione probabilistica in questo modo, otteniamo un vantaggio importante: possiamo includere facilmente altri modelli, anche quelli che gestiscono le non linearità, all’interno dello stesso quadro probabilistico. In questo modo applichiamo tecniche simili per ricavare risultati anche con altri modelli, come nel metodo della massima verosimiglianza.
Quando definiamo \({\bf x} = (1, x)\), creiamo un grafico bidimensionale \({\bf x} = (1, x)\) con x e y per visualizzare questa distribuzione congiunta. Per farlo, impostiamo i parametri \(\beta = (\beta_0, \beta_1)\) e \(\sigma^2\), che costituiscono i parametri di \(\theta\). Qui sotto includiamo uno script Python che utilizza matplotlib per rappresentare graficamente la distribuzione
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
if __name__ == "__main__":
# Set up the X and Y dimensions
fig = plt.figure()
ax = fig.gca(projection='3d')
X = np.arange(0, 20, 0.25)
Y = np.arange(-10, 10, 0.25)
X, Y = np.meshgrid(X, Y)
# Create the univarate normal coefficients
# of intercep and slope, as well as the
# conditional probability density
beta0 = -5.0
beta1 = 0.5
Z = norm.pdf(Y, beta0 + beta1*X, 1.0)
# Plot the surface with the "coolwarm" colormap
surf = ax.plot_surface(
X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0, antialiased=False
)
# Set the limits of the z axis and major line locators
ax.set_zlim(0, 0.4)
ax.zaxis.set_major_locator(LinearLocator(5))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
# Label all of the axes
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('P(Y|X)')
# Adjust the viewing angle and axes direction
ax.view_init(elev=30., azim=50.0)
# Plot the probability density
plt.show()
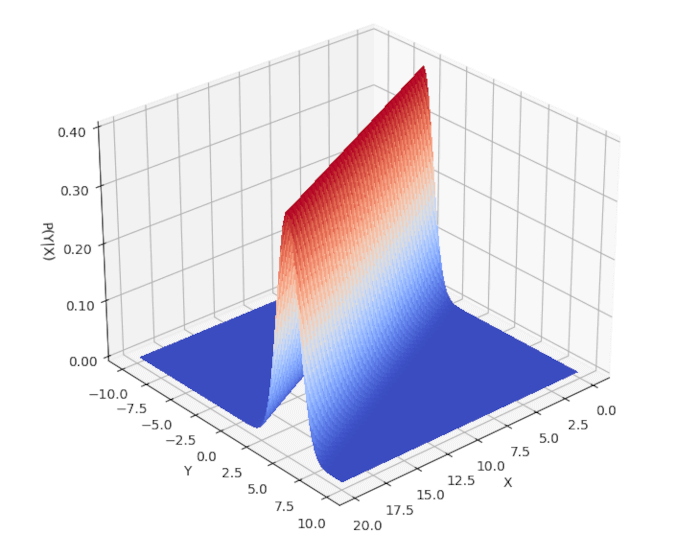
Risulta chiaro che la risposta \(y\) dipende linearmente da \(x\). Tuttavia, possiamo anche verificare l’elemento probabilistico del modello osservando come la probabilità si distribuisca normalmente attorno alla risposta lineare.
Estensione della funzione di base
L’approccio probabilistico ci permette di modellare facilmente relazioni non lineari: ci basta sostituire il vettore delle feature \(x\) con una funzione di trasformazione specifica \(\phi({\bf x})\):
\(\begin{eqnarray}p(y \mid {\bf x}, {\bf \theta}) = \mathcal(y \mid \beta^T \phi({\bf x}), \sigma^2)\end{eqnarray}\)
Se consideriamo \({\bf x} = (1, x_1, x_2, x_3)\), possiamo definire una \(\phi\) che includa termini di ordine superiore e incrociati, ad esempio:
\(\begin{eqnarray}\phi({\bf x}) = (1, x_1, x_1^2, x_2, x^2_2, x_1 x_2, x_3, x_3^2, x_1 x_3, \ldots)\end{eqnarray}\)
Notiamo che questa funzione risulta non lineare nelle feature, \(x\), ma rimane lineare nei parametri, \({\bf \beta}\). Perciò la consideriamo comunque una regressione lineare.
Quando utilizziamo una funzione di trasformazione \(\phi\), introduciamo quella che chiamiamo estensione della funzione di base, utile per estendere la regressione lineare a molte configurazioni di dati non lineari.
Numerose tecniche di apprendimento supervisionato avanzato ci aiutano a cogliere le non linearità. Nelle lezioni successive esploriamo una di queste tecniche, le Support Vector Machines, utilizzando il cosiddetto “trucco del kernel”.
Metodo della massima verosimiglianza
In questa lezione descriviamo come scegliamo i coefficienti di regressione lineare ottimali, cioè i parametri \(\beta\), per adattarli al meglio ai dati. Nel caso univariato parliamo di “trovare la retta di migliore adattamento”, ma in contesti multivariati, come quando utilizziamo un vettore delle feature \({\bf x} \in \mathbb{R}^{p+1}\), puntiamo a determinare “l’iperpiano p-dimensionale di migliore adattamento”.
Applichiamo principalmente il metodo della massima verosimiglianza per stimare i parametri dei modelli statistici. Questo approccio rappresenta lo strumento fondamentale nell’inferenza statistica e ci consente di ottimizzare il modello rispetto ai dati osservati.
Verosimiglianza e verosimiglianza logaritmica negativa
L’idea fondamentale è: se il modello ha generato i dati, quali parametri ha utilizzato con maggiore probabilità? Cioè, qual è la probabilità di osservare i dati \(\mathcal{D}\) dato uno specifico insieme di parametri \({\bf \theta}\)? Anche in questo caso affrontiamo un problema di densità di probabilità condizionata. Cerchiamo i valori di \({\bf \theta}\) che massimizzano \(p(\mathcal{D} \mid {\bf \theta})\). Questo CPD prende il nome di verosimiglianza, come abbiamo visto nella lezione introduttiva sulla statistica bayesiana.
Formuliamo questo problema come la ricerca della moda di \(p(\mathcal{D} \mid {\bf \theta})\), che definiamo come \(\hat{{\bf \theta}}\). Per semplificare i calcoli, massimizziamo il logaritmo naturale del CPD invece del CPD stesso:
\(\begin{eqnarray}\hat{{\bf \theta}} = \text{argmax}_{\theta} \log p(\mathcal{D} \mid {\bf \theta})\end{eqnarray}\)
Nei problemi di regressione lineare assumiamo che i vettori delle feature siano indipendenti e identicamente distribuiti (iid). Questo ci permette di affrontare più facilmente il problema della log-verosimiglianza, sfruttando le proprietà del logaritmo naturale. Poiché dobbiamo calcolare derivate, risulta più semplice farlo su somme piuttosto che su prodotti, da cui l’uso del logaritmo:
\(\begin{eqnarray}\mathcal{l}({\bf \theta}) &:=& \log p(\mathcal{D} \mid {\bf \theta}) \\ &=& \log \left( \prod_{i=1}^{N} p(y_i \mid {\bf x}_i, {\bf \theta}) \right) \\ &=& \sum_{i=1}^{N} \log p(y_i \mid {\bf x}_i, {\bf \theta})\end{eqnarray}\)
Per rendere i calcoli più semplici, preferiamo minimizzare il negativo della log-verosimiglianza piuttosto che massimizzare la log-verosimiglianza. Quindi, applichiamo un segno meno alla log-verosimiglianza per ottenere la log-verosimiglianza negativa (NLL):
\(\begin{eqnarray}\text{NLL} ({\bf \theta}) = – \sum_{i=1}^{N} \log p(y_i \mid {\bf x}_i, {\bf \theta})\end{eqnarray}\)
Minimizzando questa funzione, applichiamo il metodo della massima verosimiglianza per stimare i coefficienti \(\beta\) con i minimi quadrati ordinari.
Minimi quadrati ordinari
Vogliamo trovare l’insieme ottimale di coefficienti \(\beta\) che molto probabilmente spiegano i dati del nostro problema di addestramento. Questi coefficienti devono formare un iperpiano di “best fit” attraverso i dati. Seguiamo i seguenti passi:
- Applichiamo la definizione della distribuzione normale per estendere la funzione di verosimiglianza logaritmica negativa.
- Usiamo le proprietà dei logaritmi per riformulare il problema come somma residua dei quadrati (RSS), equivalente alla somma dei residui su tutte le osservazioni.
- Scriviamo i residui in forma matriciale creando la matrice X dei dati con dimensioni \(N \times (p+1)\) e rappresentiamo l’RSS con un’equazione matriciale.
- Calcoliamo la derivata di questa equazione matriciale rispetto al vettore dei parametri \(\beta\) e la poniamo uguale a zero (con opportune ipotesi su X).
- Risolvendo l’equazione otteniamo \(\hat{\beta}_\text{OLS}\), la stima dei minimi quadrati ordinari.
Seguiamo gli approcci descritti nelle fonti [2] e [3]. Espandiamo l’NLL usando la formula della distribuzione normale:
\(\begin{eqnarray}\text{NLL} ({\bf \theta}) &=& – \sum_{i=1}^{N} \log p(y_i \mid {\bf x}_i, {\bf \theta}) \\ &=& – \sum_{i=1}^{N} \log \left[ \left(\frac{1}{2 \pi \sigma^2}\right)^{\frac{1}{2}} \exp \left( – \frac{1}{2 \sigma^2} (y_i – {\bf \beta}^{T} {\bf x}_i)^2 \right)\right] \\ &=& – \sum_{i=1}^{N} \frac{1}{2} \log \left( \frac{1}{2 \pi \sigma^2} \right) – \frac{1}{2 \sigma^2} (y_i – {\bf \beta}^T {\bf x}_i)^2 \\ &=& – \frac{N}{2} \log \left( \frac{1}{2 \pi \sigma^2} \right) – \frac{1}{2 \sigma^2} \sum_{i=1}^N (y_i – {\bf \beta}^T {\bf x}_i)^2 \\ &=& – \frac{N}{2} \log \left( \frac{1}{2 \pi \sigma^2} \right) – \frac{1}{2 \sigma^2} \text{RSS}({\bf \beta})\end{eqnarray}\)
La quantità \(\text{RSS}({\bf \beta}) := \sum_{i=1}^N (y_i – {\bf \beta}^T {\bf x}_i)^2\) rappresenta la somma residua dei quadrati, nota anche come somma degli errori quadrati (SSE).
Dato che il primo termine è costante, ci concentriamo nel minimizzare l’RSS per ottenere la stima ottimale del parametro. Con il metodo della massima verosimiglianza, procediamo a semplificare la formula scrivendo il termine in forma matriciale. Considerando la matrice X con dimensioni \(N \times (p+1)\), scriviamo l’RSS come:
\(\begin{eqnarray}\text{RSS}({\bf \beta}) = ({\bf y} – {\bf X}{\bf \beta})^T ({\bf y} – {\bf X}{\bf \beta})\end{eqnarray}\)
Ora deriviamo questo termine rispetto alla variabile \({\bf \beta}\):
\(\begin{eqnarray}\frac{\partial RSS}{\partial \beta} = -2 {\bf X}^T ({\bf y} – {\bf X} \beta)\end{eqnarray}\)
Prima di procedere, verifichiamo una condizione fondamentale: la matrice \({\bf X}^T {\bf X}\) deve essere definita positivamente. Questo accade solo se le osservazioni superano le dimensioni. In caso contrario (come spesso capita in ambienti ad alta dimensione), non possiamo determinare un unico insieme di coefficienti \(\beta\) e l’equazione matriciale non risulta valida.
Quando \({\bf X}^T {\bf X}\) è definita positivamente, poniamo a zero la derivata e ricaviamo \(\beta\):
\(\begin{eqnarray}{\bf X}^T ({\bf y} – {\bf X} \beta) = 0\end{eqnarray}\)
La soluzione di questa equazione matriciale ci fornisce \(\hat{\beta}_\text{OLS}\):
\(\begin{eqnarray}\hat{\beta}_\text{OLS} = ({\bf X}^{T} {\bf X})^{-1} {\bf X}^{T} {\bf y}\end{eqnarray}\)
Attraverso il metodo della massima verosimiglianza otteniamo così una stima coerente ed efficiente dei parametri del nostro modello.
Conclusioni
Ora che abbiamo illustrato il metodo della massima verosimiglianza per ottenere le stime OLS, possiamo analizzare cosa accade quando lavoriamo in ambienti ad alta dimensione (come spesso capita con i dati del mondo reale) e la matrice \({\bf X}^T {\bf X}\) risulta non invertibile. In questi casi adottiamo tecniche di selezione di sottoinsiemi e restringimento per ridurre la dimensionalità del problema. Approfondiamo questi aspetti nella prossima lezione.
Nota bibliografica
In [1] troviamo un’introduzione elementare alla regressione lineare, insieme al restringimento, alla regolarizzazione e alla riduzione dimensionale, nel contesto dell’apprendimento supervisionato. In [2] approfondiamo queste tecniche in modo molto più rigoroso, includendo anche gli sviluppi più recenti. In [3] adottiamo un approccio probabilistico (principalmente bayesiano) alla regressione lineare, e ricaviamo in modo completo la stima tramite il metodo della massima verosimiglianza con i minimi quadrati ordinari, discutendo ampiamente anche la contrazione e la regolarizzazione. In [4] esploriamo esempi pratici di regressione lineare in contesti di alta dimensionalità, soffermandoci su riduzione della dimensione e minimi quadrati parziali.
Riferimenti
- [1] James, G., Witten, D., Hastie, T., Tibshirani, R. (2013) An Introduction to Statistical Learning, Springer
- [2] Hastie, T., Tibshirani, R., Friedman, J. (2009) Gli elementi dell’apprendimento statistico, Springer
- [3] Murphy, KP (2012) Apprendimento automatico Una prospettiva probabilistica, MIT Press
- [4] Kuhn, M., Johnson, K. (2013) Modellazione predittiva applicata, Springer