In questa lezione introduciamo le reti neurali artificiali e il perceptron e l’applicazione nel trading quantitativo. Queste sono tecniche avanzate di deep learning.
La finanza quantitativa rappresenta un settore estremamente competitivo a livello istituzionale. Gli hedge fund quantistici competono per ottenere grandi allocazioni e dimostrano costantemente il proprio valore per attrarre nuovi asset in gestione. Questo ci spinge a investire molte risorse in ricerca e sviluppo per scoprire nuove fonti di rendimento non correlato, corretto per il rischio, da offrire ai nostri clienti. I fondi e i rispettivi trading desk cercano continuamente nuove opportunità di alpha. Spesso le troviamo in mercati emergenti, attraverso dati innovativi o grazie ad algoritmi predittivi più efficaci.
Negli ultimi anni abbiamo osservato come gran parte del settore degli hedge fund quantistici abbia concentrato l’attenzione sui dati alternativi come leva per generare nuovi alpha. Questi dati, spesso non strutturati, risultano inadatti ai classici modelli basati su serie temporali. Ci impegniamo a sfruttare metodologie capaci di estrarre valore da questi dataset e trasformarli in segnali predittivi efficaci. Tra i campi più promettenti emersi di recente troviamo il deep learning.
Il deep learning ha conquistato anche l’interesse dei trader retail. L’espansione dei software open source, l’aumento della disponibilità di dati e l’accesso a hardware potente a costi contenuti ci hanno spinti a sviluppare strategie di trading basate su modelli di deep learning.
Nonostante le API dei moderni framework di deep learning risultino semplici da usare, affrontiamo comunque una curva di apprendimento significativa prima di riuscire a condurre ricerche efficaci nel trading quantitativo con questi approcci.
Introduzione
Quando lavoriamo con modelli predittivi complessi, non possiamo semplicemente “copiare e incollare” codice open source sperando di ottenere una strategia di trading robusta. Occorre comprendere a fondo i modelli per evitare errori comuni, come l’overfitting.
In questa nuova serie di lezioni esploriamo i modelli di deep learning, partendo dalla teoria dei modelli più diffusi per poi descrivere implementazioni solide, da utilizzare e adattare per i nostri obiettivi di trading.
Molti tutorial di deep learning saltano direttamente al codice. Sebbene questa sia una modalità utile per casi semplici, come la classificazione di immagini, nel contesto della finanza quantitativa non basta: un errore di modellazione può comprometterne totalmente la redditività.
Per questo motivo, su TradingQuant diamo grande importanza sia alla teoria che alla pratica, così da fornire una visione completa dell’argomento e aiutarci a ridurre i rischi associati a implementazioni errate dei modelli.
In questa lezione iniziamo presentando i modelli di reti neurali artificiali (ANN). Spieghiamo come si ispirano alle reti neurali biologiche e introduciamo uno dei primi modelli di rete: il perceptron.
Nelle lezioni successive, utilizziamo il modello percettronico come base per costruire reti neurali profonde più avanzate, come i percettroni multistrato (MLP), dimostrandone la potenza su problemi di deep learning complessi.
Reti neurali artificiali
Il deep learning potrebbe sembrare una disciplina recente, ma la ricerca in questo ambito è iniziata già negli anni ’40. Così come il volo degli uccelli ha ispirato lo sviluppo del volo artificiale, la struttura del cervello umano ci ha spinti a tentare di replicare l’intelligenza con architetture neurali simili.
Lo stesso neurone ci ha ispirati nello sviluppo di reti di neuroni computazionali, che combiniamo per eseguire calcoli sofisticati attraverso strutture di rete relativamente semplici.
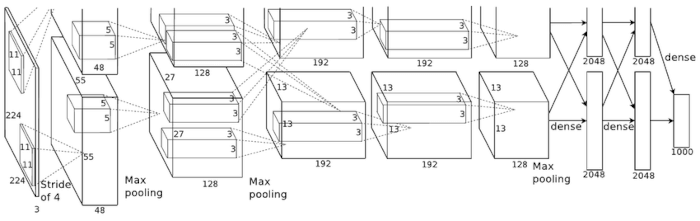
La struttura della corteccia cerebrale ha influenzato in modo significativo alcune architetture di reti neurali profonde, come la Convolutional Neural Network (CNN), che approfondiamo in una lezione successiva.
La ricerca sulle reti neurali artificiali, o reti di neuroni computazionali, ha attraversato fasi di forte espansione e finanziamento, alternate a periodi di stallo conosciuti come “Inverni AI”, durante i quali le aspettative verso questa tecnologia hanno spesso superato i risultati effettivi.
Questa dinamica dipendeva in parte da modelli ancora troppo semplici e complessi da addestrare in tempi ragionevoli. Un altro fattore importante riguardava l’elevato costo necessario per acquisire, archiviare ed elaborare grandi quantità di dati utili per ottenere risultati soddisfacenti.
Diffusione delle reti neurali artificiali
Negli ultimi anni abbiamo superato in gran parte queste difficoltà. Questo ha innescato una crescita esplosiva nella ricerca sulle ANN. L’introduzione delle Graphics Processing Unit (GPU) ha reso possibile l’addestramento a basso costo. La diffusione di Internet ha reso disponibili enormi volumi di dati. Abbiamo inoltre migliorato costantemente sia gli algoritmi di addestramento che le architetture dei modelli.
Questa convergenza di fattori ci ha permesso di ottenere risultati all’avanguardia su numerosi problemi complessi grazie a modelli di deep learning, che un tempo consideravamo intrattabili.
Anche se la storia della ricerca sulle reti neurali artificiali rappresenta un argomento affascinante, in questa lezione ci concentriamo sull’uso pratico di questi strumenti, così come fanno i professionisti del trading quantitativo, per generare rendimenti superiori rispetto al rischio assunto. Non approfondiremo quindi l’evoluzione storica delle reti neurali artificiali.
Chi desidera esplorare in dettaglio gli sviluppi storici delle reti neurali artificiali può consultare la sezione Tendenze storiche nell’apprendimento profondo contenuta nel libro Deep Learning [1].
Iniziamo presentando uno dei modelli ANN più semplici in assoluto: il perceptron.
Il Perceptron
In questa sezione introduciamo il perceptron [2], uno dei modelli più antichi e basilari di rete neurale artificiale. Anche se risulta estremamente semplice rispetto agli standard attuali del deep learning, i concetti su cui si basa trovano applicazione anche in architetture moderne e sofisticate di deep learning.
Il perceptron rappresenta un algoritmo di classificazione binaria supervisionata, che Frank Rosenblatt ha sviluppato nel 1957. Questo modello assegna ciascun dato di input a uno di due stati distinti, utilizzando una procedura di addestramento basata su dati precedenti.
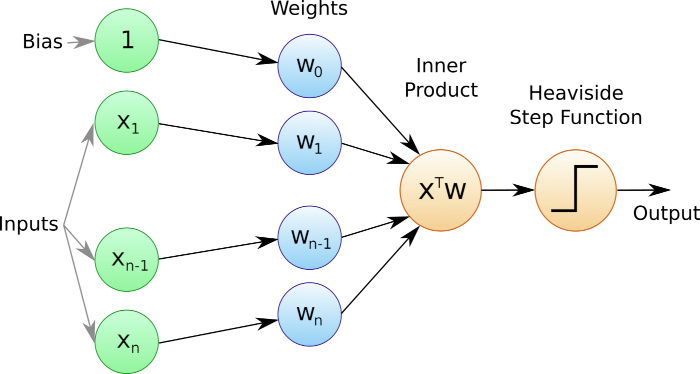
Il perceptron partiziona i dati di input tracciando un confine decisionale lineare. Applichiamo una procedura simile con un altro algoritmo di apprendimento supervisionato, noto come classificatori di vettori di supporto, che abbiamo già trattato in una lezione precedente.
Consideriamo una serie di feature scalari in input, aggiungiamo un termine costante di bias e assegniamo pesi a ciascun input. Calcoliamo quindi una combinazione lineare di pesi e input. Infine, applichiamo una funzione di attivazione che assegna allo specifico insieme di input una classe di appartenenza.
Funzioni di attivazione per il Perceptron
In questo modello di reti neurali artificiali adottiamo una funzione gradino che restituisce uno tra due valori distinti (oppure tre nel caso della funzione Segno), in base al valore della combinazione lineare.
Scegliamo spesso come funzione gradino la funzione Heaviside oppure la funzione Segno.
La funzione Heaviside, dal nome di Oliver Heaviside, è la seguente:
\(\begin{eqnarray}h(z) = \begin{cases}
0 & \text{if $z < 0$} \\
1 & \text{if $z \geq 0$}
\end{cases}\end{eqnarray}\)
Restituiamo 0 quando la combinazione lineare z è minore di 0, altrimenti restituiamo 1.
La funzione Segno è definita come segue:
\(\begin{eqnarray}\text{sgn}(z) = \begin{cases}
-1 & \text{if $z < 0$} \\ 0 & \text{if $z = 0$} \\ 1 & \text{if $z > 0$}
\end{cases}\end{eqnarray}\)
Quindi restituiamo -1 se z è minore di 0, restituiamo 0 se z è uguale a 0, altrimenti restituiamo +1.
Algoritmo per il Perceptron
Applichiamo la seguente procedura matematica per classificare un insieme di dati di input:
- Per un vettore di input x, con componenti \(x_i\) dove \(i \in \{1,\ldots,n\}\), calcoliamo il prodotto scalare tra x e il vettore dei pesi w per ottenere la somma ponderata \({\bf x}^T {\bf w}\).
- Aggiungiamo il termine di distorsione b a questa somma ponderata per calcolare \(z = {\bf x}^T {\bf w} + b\).
- Applichiamo la funzione gradino appropriata per determinare l’etichetta di classe degli input.
Quando usiamo la funzione di attivazione di Heaviside, possiamo riassumere l’algoritmo delle reti neurali artificiali con la seguente funzione:
\(\begin{eqnarray}
f(z) = \begin{cases}
1 & \text{if ${\bf x}^T {\bf w} + b > 0$} \\
0 & \text{otherwise}
\end{cases}
\end{eqnarray}\)
In pratica, se la somma pesata degli input (incluso il bias) supera lo zero, assegniamo l’etichetta 1; altrimenti assegniamo l’etichetta 0.
In alcuni manuali aggiungiamo il termine bias al vettore dei pesi w mediante un componente \(w_0\). Per farlo, inseriamo un componente \(x_0\) nel vettore di input, sempre impostato su uno: \(x_0=1\). Possiamo quindi riscrivere l’algoritmo come segue:
\(\begin{eqnarray}
f(z) = \begin{cases}
1 & \text{if ${\bf x}^T {\bf w} > 0$} \\
0 & \text{otherwise}
\end{cases}
\end{eqnarray}\)
Pur risultando più preciso, dobbiamo sempre tenere presente che il termine di bias rientra comunque nella somma pesata come uno dei suoi componenti.
Perché abbiamo bisogno di un termine bias?
A questo punto possiamo chiederci: perché includere un termine bias? Geometricamente, il confine decisionale lineare rappresenta una linea (o iperpiano) che divide la regione in due sottoregioni esclusive.
Se omettiamo il termine bias, costringiamo questa linea (o iperpiano) a passare per l’origine. Questo vincolo può compromettere gravemente le prestazioni predittive, oppure renderle inutili, se il confine decisionale reale non attraversa l’origine. Perciò includiamo sempre un termine bias per garantire flessibilità geometrica nel modello.
Conclusione
Anche se questo algoritmo di classificazione ci guida chiaramente nel classificare i dati di input, non ci dice come impostare correttamente i pesi e il bias affinché l’algoritmo funzioni in modo efficace.
E’ necessario addestrare i percettroni delle reti neurali artificiali per determinare l’insieme ottimale di pesi e distorsioni utili alla classificazione lineare. La procedura di addestramento prevede di impilare più percettroni insieme per costruire percettroni multistrato adatti sia a problemi di regressione che di classificazione.
Riferimenti
- [1] Goodfellow, I.J., Bengio, Y., Courville, A. (2016) Deep Learning, MIT Press
- [2] Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65, 386-408.
- [3] Géron, A. (2019) Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Ed., O’Reilly Media
- [4] Krizhevsky, A., Sutskever, I., Hinton, G. (2012) “ImageNet Classification with Deep Convolutional Neural Networks”, Advances in Neural Information Processing Systems 25 (NIPS 2012)

