In questa lezione esploriamo come applicare il filtro di Kalman per stimare l’hedge ratio dinamico tra ETF. A questo scopo utilizziamo la libreria pykalman di Python, così da stimare dinamicamente la pendenza e l’intercetta — e quindi il rapporto di copertura — tra una coppia di ETF.
Il filtro di Kalman ci consente di svolgere proprio questa operazione. Nella lezione precedente abbiamo analizzato a fondo il filtro di Kalman e il suo utilizzo come processo di aggiornamento bayesiano.
Introduzione
Nel trading quantitativo possiamo analizzare due asset cointegrati e utilizzare un approccio mean-reverting per costruire una strategia operativa. Per farlo, eseguiamo una regressione lineare tra i due asset (come due ETF) e sfruttiamo i coefficienti stimati per determinare le quantità con cui assumere posizioni long e short entro specifiche soglie.
Una sfida importante in questa strategia è la variazione nel tempo dei parametri strutturali, come hedge ratio dinamico tra ETF. Poiché questi parametri evolvono durante il ciclo della strategia, risulta utile adottare un meccanismo che aggiorni dinamicamente l’hedge ratio per migliorarne la redditività.
Per affrontare questo problema, possiamo adottare una regressione lineare mobile su una finestra temporale che si aggiorna a ogni nuova barra. Così facendo, i coefficienti di pendenza e intercetta seguono l’evoluzione della relazione di cointegrazione. Tuttavia, in questo modo introduciamo un nuovo parametro — la lunghezza della finestra — che dobbiamo ottimizzare, ad esempio tramite cross-validation.
Un’alternativa più avanzata prevede l’uso di un modello dello spazio degli stati. In questo schema consideriamo il “vero” rapporto di copertura come una variabile nascosta e stimiamo il suo valore attraverso osservazioni rumorose, ossia i prezzi degli asset.
Breve riepilogo del filtro di Kalman
Nella lezione precedente abbiamo già illustrato le basi matematiche e le formule del filtro di Kalman. Qui ne riassumiamo i concetti chiave.
Usiamo un modello dello spazio degli stati con due equazioni matriciali. La prima, detta equazione di stato o di transizione, descrive l’evoluzione delle variabili di stato \(\theta_t\) nel tempo. La matrice di transizione \(G_t\) e il rumore di sistema \(w_t\), entrambi variabili nel tempo, modellano questa dinamica:
\(\begin{eqnarray}\theta_t = G_t \theta_{t-1} + w_t\end{eqnarray}\)
Poiché gli stati risultano spesso non osservabili, lavoriamo sulle osservazioni \(y_t\), definite da un’equazione che combina una parte deterministica, data dalla matrice di osservazione \(F_t\), e un rumore di misura \(v_t\):
\(\begin{eqnarray}y_t = F_t \theta_t + v_t \end{eqnarray}\)
Per un approfondimento sul modello dello spazio degli stati e sul filtro di Kalman, rimandiamo alla lezione precedente.
Incorporare la regressione lineare in un filtro di Kalman
A questo punto ci chiediamo come sfruttare il modello dello spazio degli stati per integrare una regressione lineare.
Come descritto nella lezione sul MLE per la regressione lineare, una regressione multipla prevede che l’output \(y\) sia funzione lineare degli input \(x\):
\(\begin{eqnarray}y({\bf x}) = \beta^T {\bf x} + \epsilon\end{eqnarray}\)
dove \(\beta^T = (\beta_0, \beta_1, \ldots, \beta_p)\) rappresenta il vettore dei coefficienti (intercetta \(\beta_0\) e pendenze \(\beta_i\)) e \(\epsilon \sim \mathcal{N}(\mu, \sigma^2)\) è il termine di errore.
Nel nostro contesto unidimensionale, possiamo riscrivere \(\beta^T = (\beta_0, \beta_1)\) e \({\bf x} = \begin{pmatrix} 1 \\ x \end{pmatrix}\).
Consideriamo gli stati nascosti del sistema come il vettore \(\beta^T\), cioè l’intercetta e la pendenza. Supponiamo che i valori di domani siano uguali a quelli di oggi più un rumore casuale: questo li rende una passeggiata casuale, come descritto nella lezione sul rumore bianco e le passeggiate casuali:
\(\begin{eqnarray}\beta_{t+1} ={\bf I} \beta_{t} + w_t\end{eqnarray}\)
In questo caso, impostiamo la matrice di transizione \(G_t\) come matrice identità bidimensionale \({\bf I}\), completando così la metà del modello. A questo punto scegliamo uno degli ETF come osservazione e iniziamo ad applicare il filtro.
Hedge Ratio dinamico tra ETF
Vediamo un’applicazione del filtro di Kalman per gestire hedge ratio dinamico tra ETF. Per formare l’equazione di osservazione è necessario scegliere una delle serie di prezzi dell’ETF come variabile “osservata”, \(y_t\), e la serie dell’altro ETF come formulazione di regressione lineare \(x_t\) descritta in precedenza:
\(\begin{eqnarray}y_t &=& F_t {\bf x}_t + v_t \\
&=& (\beta_0, \beta_1 ) \begin{pmatrix} 1 \\ x_t \end{pmatrix} + v_t\end{eqnarray}\)
Quindi abbiamo la regressione lineare riformulata come un modello dello spazio degli stati, che ci consente di stimare l’intercetta e la pendenza quando arrivano nuovi dati di prezzo tramite il filtro di Kalman.
TLT ed ETF
Prenderemo in considerazione due ETF a reddito fisso, ovvero iShares 20+ Year Treasury Bond ETF (TLT) e iShares 3-7 Year Treasury Bond ETF (IEI) .
Entrambi questi ETF replicano la performance di obbligazioni del Tesoro statunitensi di durata variabile e, in quanto tali, sono entrambi esposti a fattori di mercato simili. Analizziamo il loro comportamento di regressione negli ultimi cinque anni circa.
Grafico a dispersione dei prezzi degli ETF
Usiamo una varietà di librerie Python, tra cui numpy, matplotlib, pandas e pykalman per analizzare il comportamento di una regressione lineare dinamica tra questi due titoli. Come per tutti i programmi Python, il primo compito è importare le librerie necessarie:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yfinance as yf
from pykalman import KalmanFilter
Nota: probabilmente dobbiamo eseguire pip install pykalman per installare la libreria PyKalman.
Scriviamo ora la funzione draw_date_coloured_scatterplot per generare un grafico a dispersione dei prezzi di chiusura rettificati dell’asset. Usiamo la mappa dei colori “Yellow To Red” di matplotlib, dove il giallo indica le coppie di prezzi più datate, mentre il rosso evidenzia quelle più recenti.
def draw_date_coloured_scatterplot(etfs, prices):
"""
Creare un grafico scatterplot dei prezzi di due ETF, che è
colorato dalle date dei prezzi per indicare il cambiamento
della relazione tra le due serie di prezzi
"""
# Creare a una mappa di colore da giallo a rosso dove il giallo
# indica le date più vecchie e il rosso indica le date recenti
# early dates and red indicates later dates
plen = len(prices)
colour_map = plt.cm.get_cmap('YlOrRd')
colours = np.linspace(0.1, 1, plen)
# Creare l'oggetto scatterplot
scatterplot = plt.scatter(
prices[etfs[0]], prices[etfs[1]],
s=30, c=colours, cmap=colour_map,
edgecolor='k', alpha=0.8
)
# Aggiungere una barra di colori per la colorazione dei dati ed
# impostare le etichette dell'asse corrispondente
colourbar = plt.colorbar(scatterplot)
colourbar.ax.set_yticklabels(
[str(p.date()) for p in prices[::plen // 9].index]
)
plt.xlabel(prices.columns[0])
plt.ylabel(prices.columns[1])
plt.show()
colour_map, colours e scatterplot. Otteniamo così il grafico desiderato.
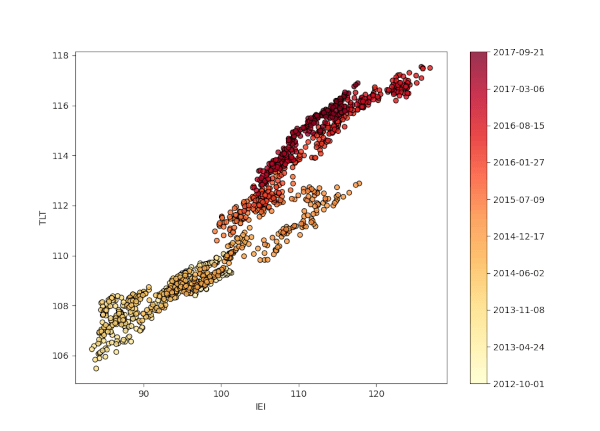
Pendenza e intercetta variabili nel tempo
Proseguiamo con il calcolo dell’hedge ratio dinamico tra ETF, regolando nel tempo pendenza e intercetta tra TFT e IEI grazie a PyKalman. Questa funzione risulta più complessa, quindi la spieghiamo passo dopo passo.
Per prima cosa definiamo la variabile delta, che controlla la covarianza di transizione del rumore di sistema. Nella lezione sul filtro di Kalman l’abbiamo indicata con \(W_t\). Moltiplichiamo questo valore per la matrice identità bidimensionale.
A questo punto costruiamo la matrice di osservazione. Come visto in precedenza, si tratta di un vettore con i prezzi di TFT e una sequenza di valori unitari. Usiamo il metodo vstack di numpy per impilare verticalmente le due serie in un singolo vettore colonna, che poi trasponiamo.
Ora creiamo un’istanza della classe KalmanFilter di PyKalman. Specifichiamo la dimensione dell’osservazione (1) e quella dello stato (2, poiché stimiamo pendenza e intercetta della regressione lineare).
Impostiamo la media iniziale dello stato a zero sia per l’intercetta che per la pendenza, e scegliamo la matrice identità bidimensionale come covarianza iniziale. Anche le matrici di transizione sono identità bidimensionali.
Specifichiamo poi la matrice di osservazione in obs_mat e la sua covarianza (uguale a 1). La matrice di covarianza di transizione, determinata da delta, è memorizzata in trans_cov.
Una volta ottenuta l’istanza kf del filtro Kalman, la usiamo per applicare il filtro ai prezzi rettificati di IEI. Otteniamo così la media degli stati (pendenza e intercetta) e le rispettive covarianze.
Raccogliamo tutto nella funzione calc_slope_intercept_kalman:
def calc_slope_intercept_kalman(etfs, prices):
"""
Utilizzo del filtro Kalman dal pacchetto pyKalman
per calcolare la pendenza e l'intercetta della
regressione lineare dei prezzi degli ETF.
"""
delta = 1e-5
trans_cov = delta / (1 - delta) * np.eye(2)
obs_mat = np.vstack(
[prices[etfs[0]], np.ones(prices[etfs[0]].shape)]
).T[:, np.newaxis]
kf = KalmanFilter(
n_dim_obs=1,
n_dim_state=2,
initial_state_mean=np.zeros(2),
initial_state_covariance=np.ones((2, 2)),
transition_matrices=np.eye(2),
observation_matrices=obs_mat,
observation_covariance=1.0,
transition_covariance=trans_cov
)
state_means, state_covs = kf.filter(prices[etfs[1]].values)
return state_means, state_covs
prices, e tracciamo ogni colonna come grafico separato.
def draw_slope_intercept_changes(prices, state_means):
"""
Tracciare la variazione di pendenza e intercetta
dai valori calcolati dal Filtro di Kalman.
"""
pd.DataFrame(
dict(
slope=state_means[:, 0],
intercept=state_means[:, 1]
), index=prices.index
).plot(subplots=True)
plt.show()
Si ottiene il seguente grafico:
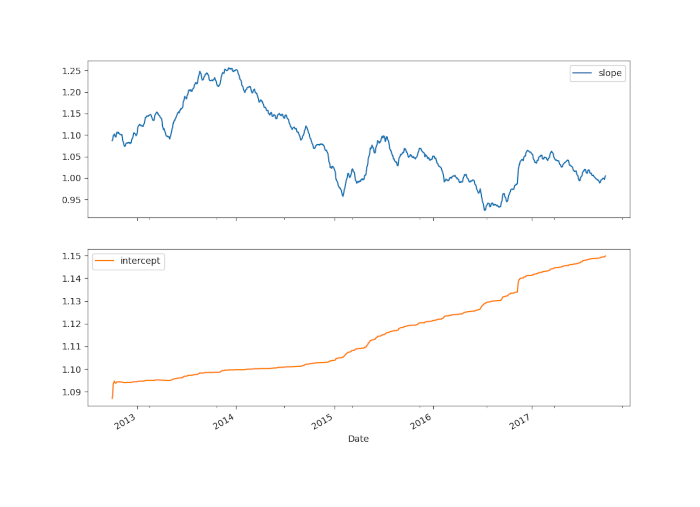
Conclusioni
Osserviamo chiaramente come la pendenza dinamica vari nel tempo, passando da circa 1,25 nel 2014 a circa 0,9 nel 2016. Usare un hedge ratio fisso per una strategia di pairs trading risulterebbe troppo rigido.
La stima della pendenza risente del rumore e la variabile delta ci permette di controllarne l’effetto. Essa regola anche la sensibilità del filtro rispetto ai cambiamenti del vero rapporto di copertura, che rimane non osservabile.
Quando sviluppiamo una strategia di trading basata su hedge ratio dinamico, dobbiamo ottimizzare il parametro delta su panieri di coppie ETF, utilizzando la convalida incrociata.
Ora che abbiamo costruito un hedge ratio dinamico tra ETF con il filtro di Kalman, possiamo sviluppare una strategia di trading concreta. Possiamo usare framework python di backtesting per testare le performance su varie coppie ETF, esplorando come variano i risultati a seconda dei parametri e dei periodi considerati.
Nota bibliografica
Abbiamo visto che molti quant trader utilizzano il filtro di Kalman per stimare regressioni lineari dinamiche. Ernie Chan lo impiega nel suo libro [1] per stimare i coefficienti tra EWA ed EWC.
Anche Aidan O’Mahony utilizza matplotlib e PyKalman per stimare i coefficienti in un suo articolo [2].
Jonathan Kinlay discute l’uso del filtro su dati simulati [3], suggerendo di applicare il filtro Kalman per attenuare segnali in presenza di rumore e aumentare l’allocazione dove il rumore è basso.
Cowpertwait e Metcalfe offrono un’introduzione al filtro Kalman in R [4].
Riferimenti
- [1] Chan, E.P. (2013). Algorithmic Trading: Winning Strategies and Their Rationale.
- [2] O’Mahony, A. (2014). Online Linear Regression using a Kalman Filter
- [3] Kinlay, J. (2015). Statistical Arbitrage Using the Kalman Filter
- [4] Cowpertwait, P.S.P. and Metcalfe, A.V. (2009). Introductory Time Series with R.
- [5] Pole, A., West, M., and Harrison, J. (1994). Applied Bayesian Forecasting.
Codice completo
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yfinance as yf
from pykalman import KalmanFilter
def draw_date_coloured_scatterplot(etfs, prices):
"""
Creare un grafico scatterplot dei prezzi di due ETF, che è
colorato dalle date dei prezzi per indicare il cambiamento
della relazione tra le due serie di prezzi
"""
plen = len(prices)
colour_map = plt.cm.get_cmap('YlOrRd')
colours = np.linspace(0.1, 1, plen)
# Creare l'oggetto scatterplot
scatterplot = plt.scatter(
prices[etfs[0]], prices[etfs[1]],
s=30, c=colours, cmap=colour_map,
edgecolor='k', alpha=0.8
)
# Aggiungere una barra di colori per la colorazione dei dati ed
# impostare le etichette dell'asse corrispondente
colourbar = plt.colorbar(scatterplot)
colourbar.ax.set_yticklabels(
[str(p.date()) for p in prices[::plen // 9].index]
)
plt.xlabel(prices.columns[0])
plt.ylabel(prices.columns[1])
plt.show()
def calc_slope_intercept_kalman(etfs, prices):
"""
Utilizzo del filtro Kalman dal pacchetto pyKalman
per calcolare la pendenza e l'intercetta della
regressione lineare dei prezzi degli ETF.
"""
delta = 1e-5
trans_cov = delta / (1 - delta) * np.eye(2)
obs_mat = np.vstack(
[prices[etfs[0]], np.ones(prices[etfs[0]].shape)]
).T[:, np.newaxis]
kf = KalmanFilter(
n_dim_obs=1,
n_dim_state=2,
initial_state_mean=np.zeros(2),
initial_state_covariance=np.ones((2, 2)),
transition_matrices=np.eye(2),
observation_matrices=obs_mat,
observation_covariance=1.0,
transition_covariance=trans_cov
)
state_means, state_covs = kf.filter(prices[etfs[1]].values)
return state_means, state_covs
def draw_slope_intercept_changes(prices, state_means):
"""
Tracciare la variazione di pendenza e intercetta
dai valori calcolati dal Filtro di Kalman.
"""
pd.DataFrame(
dict(
slope=state_means[:, 0],
intercept=state_means[:, 1]
), index=prices.index
).plot(subplots=True)
plt.show()
if __name__ == "__main__":
# Scegliere i simboli ETF symbols e il periodo temporale
# dei prezzi storici
etfs = ['TLT', 'IEI']
start_date = "2012-10-01"
end_date = "2017-10-01"
# Download dei prezzi di chiusura da Yahoo finance
prices = yf.download(etfs, start=start_date, end=end_date, auto_adjust=False)
prices = prices['Adj Close']
draw_date_coloured_scatterplot(etfs, prices)
state_means, state_covs = calc_slope_intercept_kalman(etfs, prices)
draw_slope_intercept_changes(prices, state_means)
Il codice completo per l’hedge ratio dinamico tra ETF, presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“