MODELLI AVANZATI PER IL TRADING QUANTITATIVO

Lezione 6 / 7

I Modelli di Markov Nascosti nel Trading Quantitativo

In questa lezione esploriamo la teoria matematica dei modelli di Markov nascosti (HMM) e mostriamo come applicarli al trading quantitativo e algoritmico.

Introduzione

Nel trading quantitativo affrontiamo costantemente il problema dei frequenti cambiamenti nel comportamento dei mercati finanziari, spesso improvvisi, a causa delle politiche governative, dell’ambiente normativo e di altri fattori macroeconomici. Chiamiamo questi periodi “regimi di mercato” e ci impegniamo a rilevarli, anche se il processo risulta complesso e impegnativo.

Questi regimi modificano i rendimenti degli asset alterando medie, varianze/volatilità, correlazioni seriali e covarianze. Questi effetti compromettono l’efficacia dei metodi di serie temporali basati sulla stazionarietà, generando correlazioni variabili, code grasse (curtosi elevate), eteroschedasticità e rendimenti distorti.

Per affrontare queste sfide, individuiamo e classifichiamo i regimi di mercato così da selezionare le strategie quantitative più efficaci e ottimizzarne i parametri. In questo modo, modelliamo i cambi di regime per adattare criteri di implementazione, gestione del rischio e dimensionamento della posizione.

Uno dei metodi più utilizzati per rilevare i regimi consiste nell’impiegare una tecnica di serie temporali chiamata Hidden Markov Model. Gli HMM si adattano bene a questo scopo perché ci permettono di inferire processi generativi “nascosti” analizzando osservazioni indirette e “rumorose” collegate agli stati del regime sottostante, rappresentati dai rendimenti degli asset.

Applicazioni dei modelli di Markov nascosti

Introduciamo innanzitutto il concetto di modello di Markov e la sua classificazione, che varia in base all’autonomia del sistema e alla quantità di informazioni disponibili. Poi descriviamo l’architettura dell’HMM come processo autonomo con osservazioni parziali dello stato.

Come già visto nelle precedenti lezioni sui modelli di spazio degli stati e filtro di Kalman, introduciamo i concetti di filtraggio, smoothing e previsione. Non entriamo nei dettagli degli algoritmi come il Forward Algorithm e il Viterbi Algorithm, perché ci concentriamo sull’applicazione dell’HMM alla finanza quantitativa, non sulla derivazione tecnica.

Nella prossima lezione applichiamo l’HMM a diversi asset per individuare i regimi di mercato. Integriamo poi questi dati in una serie di strategie di trading quantitative utilizzando un “gestore del rischio”, per valutare come cambia la performance del trading algoritmico con e senza la determinazione del regime.

Modelli di Markov

Prima di introdurre i modelli di Markov nascosti, presentiamo il concetto fondamentale del modello di Markov. Un modello di Markov rappresenta un processo stocastico sullo spazio degli stati con transizioni casuali tra gli stati, dove la probabilità di salto dipende esclusivamente dallo stato attuale, e non da quelli precedenti. Questo conferisce al modello la proprietà di Markov, detta anche “assenza di memoria”. I modelli Random Walk rappresentano un esempio classico di modello di Markov.

Classifichiamo i modelli di Markov in quattro categorie principali, in base all’autonomia del sistema e alla possibilità di osservare tutte o parte delle informazioni in ogni stato. La pagina dedicata su Wikipedia [1] offre una matrice utile che sintetizza queste differenze, che riportiamo qui sotto:

	Completamente osservabile	Parzialmente osservabile
Autonomo	Catena di Markov [3]	Modello Markov nascosto [2]
Controllato	Processo decisionale di Markov [3]	Processo decisionale di Markov parzialmente osservabile [4]

Modelli Autonomi

Tra i modelli più semplici, troviamo la catena di Markov, che definiamo autonoma e completamente osservabile. In questo caso, nessun agente può modificarla e tutte le informazioni risultano disponibili per ogni stato. Un esempio noto è l’algoritmo Markov Chain Monte Carlo (MCMC), molto usato nell’inferenza bayesiana computazionale.

Quando il modello resta autonomo ma diventa solo parzialmente osservabile, parliamo di Hidden Markov Model. In questo caso, il sistema contiene stati latenti non direttamente visibili, che influenzano le osservazioni. Gli stati latenti seguono la proprietà di Markov, ma non necessariamente quelli osservabili. Fuori dal contesto della finanza quantitativa, gli HMM trovano applicazione soprattutto nel riconoscimento vocale.

Modelli Controllati

Quando invece uno o più agenti possono controllare il sistema, ci troviamo nel campo del Reinforcement Learning (RL), considerato il terzo pilastro del machine learning accanto all’apprendimento supervisionato e non supervisionato. Se il sistema risulta controllabile e completamente osservabile, parliamo di Markov Decision Process (MDP).

Tra le tecniche correlate, citiamo il Q-Learning [11], utile per ottimizzare la strategia di comportamento di un agente all’interno di un MDP. Nel 2015, Google DeepMind ha sviluppato le Deep Q Networks, consentendo a un agente di apprendere a giocare ai videogiochi Atari 2600 semplicemente osservando il buffer dello schermo [12].

Nel caso in cui il sistema sia controllabile ma solo parzialmente osservabile, parliamo di Processi decisionali di Markov parzialmente osservabili (POMDP), una variante dei modelli di Reinforcement Learning. Le tecniche per risolvere i POMDP ad alta dimensione costituiscono un campo di ricerca molto attivo.

OpenAI, organizzazione non profit, dedica ampie risorse a questi problemi e ha creato un toolkit open source, l’OpenAI Gym [13], per testare direttamente nuovi agenti RL.

Sebbene il Reinforcement Learning, insieme a MDP e POMDP, esuli dallo scopo di questa lezione, approfondiremo questi modelli in altre lezioni dedicate al Deep Learning.

In questa lezione non trattiamo i processi di Markov a tempo continuo. Nel trading quantitativo, usiamo solitamente tick o barre di dati storici come unità temporali. Tuttavia, per la valutazione dei derivati, conviene adottare un approccio a tempo continuo con il calcolo stocastico.

Specifiche matematiche del modello Markov

Seguiamo da vicino la notazione e le specifiche del modello presentato da Murphy (2012) [8], anche per il modello di Markov nascosto.

Nel contesto della finanza quantitativa, analizziamo spesso le serie storiche come elemento centrale. Una tipica serie temporale si compone di una sequenza \(T\) di osservazioni discrete \(X_1, \ldots, X_T\). I modelli Markov Chain assumono che, in ogni istante \(t\), l’osservazione \(X_t\) contenga tutte le informazioni utili per prevedere gli stati futuri. Utilizzeremo questa ipotesi nella specifica seguente.

Con una formulazione probabilistica della catena di Markov, possiamo esprimere la densità congiunta della probabilità di osservare la sequenza come:

\(\begin{eqnarray}p(X_{1:T}) &=& p(X_1)p(X_2 \mid X_1)p(X_3 \mid X_2)\ldots \\
&=& p(X_1) \prod^{T}_{t=2} p(X_t \mid X_{t-1})\end{eqnarray}\)

Questa formula indica che la probabilità di osservare l’intera sequenza corrisponde alla probabilità dell’osservazione iniziale moltiplicata \(T-1\) volte per la probabilità condizionata dell’osservazione successiva, nota quella precedente. In questa lezione, assumiamo che il termine \(p(X_t \mid X_{t-1})\), ovvero la funzione di transizione, non dipenda dal tempo.

Poiché nei modelli di regime di mercato che trattiamo utilizziamo un numero finito e discreto \(K\) di regimi (o stati), ci riferiamo a una catena di Markov a stati discreti (DSMC).

Quando esistono K stati distinti in cui il modello può trovarsi in ogni istante t, possiamo descrivere la funzione di transizione come una matrice di transizione. Questa matrice definisce la probabilità di passare dallo stato j allo stato i. Formalmente, definiamo gli elementi della matrice di transizione A così:

\(\begin{eqnarray}A_{ij} = p(X_t = j \mid X_{t-1} = i)\end{eqnarray}\)

Modello a due stati

Per chiarire, consideriamo un semplice modello a due stati. Il seguente diagramma mostra gli stati come cerchi numerati, mentre gli archi rappresentano la probabilità di passare da uno stato all’altro.

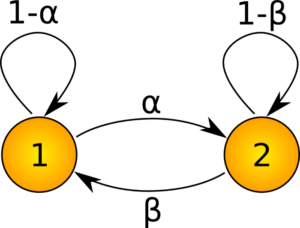
Si noti che le probabilità si sommano all’unità per ogni stato, ad es \(\alpha + (1 – \alpha) = 1\). La matrice di transizione A per questo sistema è una matrice 2×2 data da:

\(\begin{eqnarray}A = \left( \begin{array}{cc}
1-\alpha & \alpha \\
\beta & 1-\beta \end{array} \right)\end{eqnarray}\)

Per simulare i n passi di un modello DSMC generico è possibile definire n-esimo passo della matrice di transizione come:

\(\begin{eqnarray}A_{ij}(n) := p(X_{t+n} = j \mid X_t = i)\end{eqnarray}\)

Si può facilmente dimostrare che \(A(m+n)=A(m)A(n)\) e quindi che \(A(n)=A(1)^n\). Ciò significa che gli n passaggi di un modello DSMC possono essere simulati semplicemente moltiplicando ripetutamente la matrice di transizione con se stessa.

Modelli di Markov Nascosti

I modelli di Markov nascosti rappresentano una variante dei modelli di Markov in cui non possiamo osservare direttamente gli stati, poiché restano “nascosti”. Possiamo però vedere una serie di osservazioni di output associate agli stati. Per rendere il concetto più concreto in ambito finanza quantitativa, immaginiamo gli stati come “regimi” di mercato nascosti, mentre le osservazioni corrispondono ai rendimenti degli asset, che possiamo vedere direttamente.

Nei modelli di Markov, ci limitiamo a costruire una funzione di densità congiunta per le osservazioni. Definiamo una matrice di transizione invariante nel tempo, che ci consente di simulare completamente il modello.

Con i modelli di Markov nascosti, invece, definiamo un insieme di stati discreti \(z_t \in \{1,\ldots, K \}\) (spesso è sufficiente \(K \leq 3\) per identificare il regime) e utilizziamo un modello probabilistico aggiuntivo per descrivere le osservazioni, \(p({\bf x}_t \mid z_t)\), ovvero la probabilità condizionata di osservare un certo rendimento dato che lo stato corrente è \(z_t\).

In base allo stato e alle probabilità di transizione, il modello tende a restare in uno stato specifico per poi saltare improvvisamente in un altro, dove rimane per un certo tempo. Questo comportamento rispecchia esattamente ciò che vogliamo ottenere quando applichiamo questi modelli ai regimi di mercato. Non ci aspettiamo che i regimi cambino rapidamente, dato che cambiamenti normativi e fattori macroeconomici evolvono lentamente. Tuttavia, una volta avvenuto un cambiamento, ci aspettiamo che il nuovo regime persista per un po’.

Specifiche matematiche del modello Markov nascosto

La funzione di densità congiunta corrispondente all’HMM è definita nel modo seguente (utilizziamo ancora la notazione di Murphy – 2012 [8]):

\(\begin{eqnarray}p({\bf z}_{1:T} \mid {\bf x}_{1:T}) &=& p({\bf z}_{1:T}) p ({\bf x}_{1:T} \mid {\bf z}_{1:T}) \\
&=& \left[ p(z_1) \prod_{t=2}^{T} p(z_t \mid z_{t-1}) \right] \left[ \prod_{t=1}^T p({\bf x}_t \mid z_t) \right]\end{eqnarray}\)

Nella prima riga esprimiamo la probabilità congiunta di osservare tutti gli stati nascosti e le osservazioni come il prodotto tra la probabilità degli stati nascosti e quella delle osservazioni condizionate agli stati. Questo ha senso: le osservazioni non influenzano gli stati, ma gli stati nascosti influenzano indirettamente le osservazioni.

Nella seconda riga, separiamo le due distribuzioni in funzioni di transizione. La funzione di transizione degli stati è \(p(z_t \mid z_{t-1})\), mentre quella delle osservazioni, che dipendono dagli stati, è \(p({\bf x}_t \mid z_t)\).

Come fatto per i modelli di Markov, in questa lezione assumiamo che le funzioni di transizione di stato e di osservazione restino invariate nel tempo. Questo ci consente di usare la matrice di transizione A, di dimensioni \(K \times K\), in modo analogo a quanto avviene nei modelli di Markov per la parte degli stati.

Distribuzione gaussiana multivariata

Nel contesto della nostra applicazione, cioè l’osservazione dei rendimenti degli asset, lavoriamo con valori continui. Di conseguenza, la modellazione della funzione di transizione per le osservazioni risulta più complessa. La scelta più comune consiste nell’usare una distribuzione gaussiana multivariata condizionata con media \({\bf \mu}_k\) e covarianza \({\bf \sigma}_k\), come segue:

\(\begin{eqnarray}p({\bf x}_t \mid z_t = k, {\bf \theta}) = \mathcal{N}({\bf x}_t \mid {\bf \mu}_k, {\bf \sigma}_k)\end{eqnarray}\)

Vale a dire, se lo stato \(z_t\) è pari a k, allora la probabilità di osservare \({\bf x}_t\), dati i parametri del modello \(\theta\), segue una distribuzione gaussiana multivariata.

Per chiarire visivamente questi passaggi, mostriamo nel diagramma seguente come si evolvono gli stati \(z_t\) e come questi conducano indirettamente all’evoluzione delle osservazioni \({\bf x}_t\).

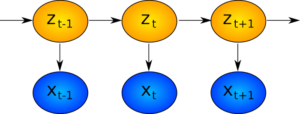
Filtraggio nei modelli di Markov nascosti

Dopo aver definito la funzione di densità congiunta, passiamo ora all’utilizzo pratico del modello. Nella modellazione dello spazio degli stati affrontiamo di solito tre compiti principali: filtraggio, smoothing e previsione. Nella lezione precedente sui modelli dello spazio degli stati e il filtro di Kalman li abbiamo descritti brevemente. Ripassiamoli ora per completezza:

Previsione – Prevediamo i valori futuri dello stato
Filtraggio – Stimiamo i valori attuali dello stato usando le osservazioni passate e presenti
Smoothing – Stimiamo i valori passati dello stato a partire dalle osservazioni disponibili

Il filtraggio e lo smoothing si somigliano, ma hanno obiettivi diversi. Con lo smoothing cerchiamo di comprendere gli stati passati sulla base delle informazioni attuali, mentre con il filtraggio ci concentriamo su ciò che accade allo stato in questo momento.

Approfondire tutti gli algoritmi per il filtraggio, lo smoothing e la previsione esula dallo scopo di questa lezione. Il nostro obiettivo resta quello di applicare i modelli di Markov nascosti per identificare il regime di mercato. Quindi ci concentriamo sul determinare quale sia l’attuale “stato di regime di mercato” usando i rendimenti degli asset fino a oggi. Proprio qui entra in gioco il filtraggio come passaggio cruciale.

Dal punto di vista matematico, ci interessa la probabilità condizionata dello stato al tempo t data la sequenza delle osservazioni fino a t, cioè vogliamo calcolare \(p(z_t \mid {\bf x}_{1:T})\). Come nel filtro di Kalman, possiamo applicare in modo ricorsivo la regola di Bayes per ottenere il filtraggio in un HMM.

Prossimi passi

Nella prossima lezione approfondiamo i modelli di Markov nascosti. Utilizziamo le librerie Python applicate ai rendimenti storici degli asset per costruire uno strumento in grado di rilevare il regime. Questo strumento lo impieghiamo nella gestione del rischio all’interno del nostro approccio di trading quantitativo.

Nota bibliografica

Una panoramica completa sui modelli di Markov, incluse le principali classificazioni e i modelli nascosti con relativi algoritmi di risoluzione, è disponibile in vari articoli introduttivi su Wikipedia [1], [2], [3], [4], [5], [6], [7].

Per un’esposizione matematica dettagliata sui modelli di Markov nascosti, comprese applicazioni al riconoscimento vocale e all’algoritmo PageRank di Google, rimandiamo a Murphy (2012) [8]. Bishop (2007) [8] propone un approccio simile a quello di Murphy, includendo la derivazione della Maximum Likelihood Estimate (MLE) per l’HMM, insieme agli algoritmi Forward-Backward e Viterbi. Concludiamo con una discussione sui Sistemi Dinamici Lineari e i filtri a particelle.

Riferimenti

Previous Lesson

Back to Course

Next Lesson