In questa lezione spieghiamo come determinare il regime di mercato con i modelli di Markov nascosti. Vediamo insieme come implementare i modelli di Markov nascosti utilizzando il linguaggio di programmazione Python. Il modo più semplice per lavorare con questi modelli in Python è la libreria hmmlearn. Impariamo a usare gli HMM per analizzare i diversi regimi che caratterizzano i mercati azionari statunitensi.
Introduzione
Nella lezione precedente abbiamo introdotto gli Hidden Markov Models. Li abbiamo contestualizzati all’interno della più ampia famiglia dei modelli di Markov. Utilizziamo questi modelli per identificare i regimi di mercato e adattare la gestione delle nostre strategie quantitative.
In particolare, abbiamo sottolineato che “la variazione dei regimi causa aggiustamenti nei rendimenti degli asset attraverso il cambiamento delle medie, delle varianze/volatilità, delle correlazioni seriali e delle covarianze, influenzando l’efficacia dei metodi di analisi delle serie temporali che si basano sulla stazionarietà“. Questo fenomeno impatta significativamente il comportamento delle strategie di trading nel corso del tempo.
In questa lezione simuliamo una serie di rendimenti del mercato in due diversi regimi: “rialzista” e “ribassista”. Applichiamo quindi un modello di Markov alla serie dei ritorni per stimare la probabilità di trovarci in un determinato regime di mercato.
Dopo aver illustrato la procedura sui dati simulati, estendiamo l’analisi applicando il modello Hidden Markov ai dati dei mercati azionari statunitensi per individuare i regimi a due stati che li caratterizzano.
Regimi di mercato con i modelli di Markov nascosti
Utilizzare gli Hidden Markov Models per rilevare i regimi di mercato rappresenta una sfida, poiché si tratta di una forma di apprendimento non supervisionato. Non disponiamo infatti di una “verità di base” o di dati etichettati su cui allenare il modello. Non sappiamo a priori quanti regimi esistano: due, tre, quattro o più regimi di mercato nascosti?
Le risposte variano in base alla classe di asset analizzata, al periodo temporale scelto e alla natura dei dati. Ad esempio, nei mercati azionari i rendimenti giornalieri mostrano spesso fasi di calma con bassa volatilità, alternate a periodi eccezionali di alta volatilità dovuti al panico o alle correzioni. Modellare questi indici con due soli stati basta? Oppure serve un terzo stato intermedio che indichi una volatilità superiore alla norma, ma non assimilabile al panico?
Quando integriamo gli Hidden Markov Models come componente di un gestore del rischio, capace di intervenire sugli ordini generati dalla strategia, dobbiamo condurre un’analisi rigorosa e comprendere a fondo la classe di asset analizzata.
Dati simulati
In questa sezione impariamo a generare dati simulati dei rendimenti partendo da distribuzioni gaussiane distinte, ciascuna delle quali rappresenta il regime di mercato “rialzista” o “ribassista”. Utilizziamo una distribuzione gaussiana con media positiva e varianza bassa per i rendimenti rialzisti, mentre per quelli ribassisti scegliamo una distribuzione gaussiana con media leggermente negativa e varianza più elevata.
Simuliamo cinque periodi distinti di regime di mercato e li uniamo in sequenza con Python. Usiamo poi il flusso complessivo dei rendimenti in un modello di Markov nascosto, così da calcolare le probabilità a posteriori degli stati di regime sulla base della sequenza osservata.
Per cominciare, installiamo le librerie yfinance e hmmlearn e le importiamo in Python. Impostiamo anche il seed casuale per garantire la coerenza dei risultati nelle repliche. In questo modo esploriamo concretamente i regimi di mercato con i modelli di Markov nascosti.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance
import hmmlearn
np.random.seed(1)
Simulazione dei regimi
In questo esempio simuliamo un mercato con due regimi, assumendo che i rendimenti di mercato siano normalmente distribuiti. Simuliamo regimi separati, ciascuno composto da \(N_k\) giorni di rendimenti. Ognuno di questi k regimi può essere rialzista o ribassista. L’obiettivo del modello Hidden Markov è identificare quando il regime passa da rialzista a ribassista e viceversa.
Consideriamo \(k=5\) e \(N_k \in [50, 150]\). Il mercato rialzista è distribuito come \(\mathcal{N}(0.1, 0.1)\) mentre il mercato ribassista è distribuito come \(\mathcal{N}(-0.05, 0.2)\). I parametri sono impostati tramite il seguente codice:
# Create the parameters for the bull and bear market returns distributions
Nk_lower = 50
Nk_upper = 150
bull_mean = 0.1
bull_var = 0.1
bear_mean = -0.05
bear_var = 0.2
# Create the list of durations (in days) for each regime
days = np.random.randint(Nk_lower, Nk_upper, 5)
# Create the various bull and bear markets returns
market_bull_1 = np.random.normal(loc=bull_mean, scale=bull_var, size=days[1])
market_bear_2 = np.random.normal(loc=bear_mean, scale=bear_var, size=days[2])
market_bull_3 = np.random.normal(loc=bull_mean, scale=bull_var, size=days[3])
market_bear_4 = np.random.normal(loc=bear_mean, scale=bear_var, size=days[4])
market_bull_5 = np.random.normal(loc=bull_mean, scale=bull_var, size=days[5])
Modello a due stati
Il codice Python per creare gli stati del regime (1 per rialzista o 2 per ribassista) e l’elenco finale dei rendimenti è il seguente:
# Create the list of true regime states and full returns list
true_regimes=np.r_[np.repeat(1, days[0]), np.repeat(2,days[1]), np.repeat(1, days[2]), np.repeat(2,days[3]), np.repeat(1,days[4])]
returns = np.r_[market_bull_1, market_bear_2, market_bull_3, market_bear_4, market_bull_5]
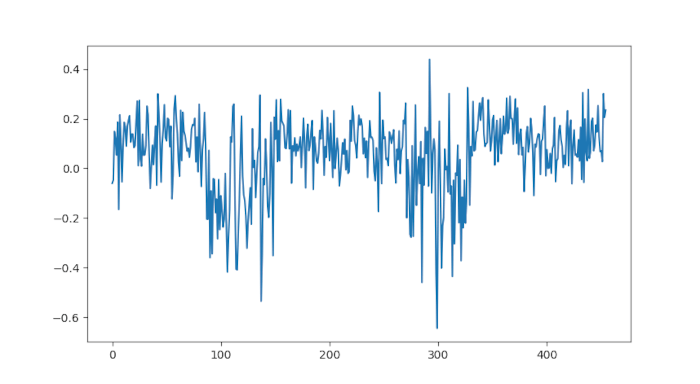
GaussianHMM della libreria hmmlearn, impostando il numero di stati pari a 2:
from hmmlearn.hmm import GaussianHMM
# Reshape dei dati per hmmlearn
X = returns.reshape(-1, 1)
# Definizione e training del modello HMM
hmm = GaussianHMM(n_components=2, covariance_type="full", n_iter=100, random_state=42)
hmm.fit(X)
# Estrazione delle probabilità posteriori
post_probs = hmm.predict_proba(X)
predicted_states = hmm.predict(X)
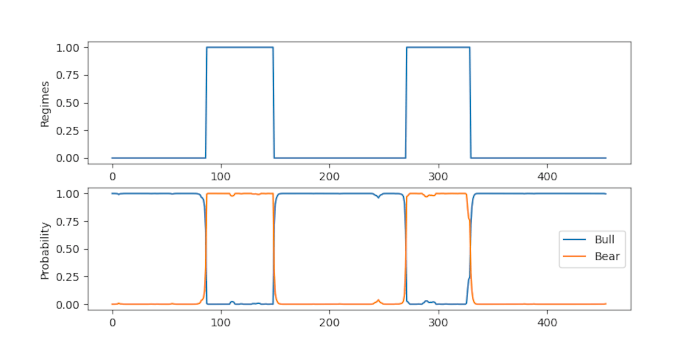
Dopo il fitting del modello è possibile tracciare il grafico delle probabilità a posteriori di trovarsi in un particolare stato di regime. La variabile post_probs contiene le probabilità a posteriori. Queste probabilità sono confrontati con i veri stati sottostanti.
Da notare che il modello Hidden Markov fa un buon lavoro nell’identificare correttamente i regimi, anche se con un certo ritardo:
fig, axs = plt.subplots(2) # Definezione di due grafici
axs[0].plot(hidden_states)
axs[0].set(ylabel='Regimes')
axs[1].plot(post_prob, label=['Bull','Bear'])
axs[1].set(ylabel='Probability')
axs[1].legend()
plt.show()
Dati finanziari
Abbiamo descritto come identificare facilmente il regime di mercato con i modelli di Markov nascosti, grazie a stati simulati da un insieme predefinito di distribuzioni gaussiane. Come abbiamo già spiegato, il problema del Regime Detection rappresenta in realtà una sfida di apprendimento non supervisionato, poiché il numero di stati resta ignoto e non esiste una “verità di base” su cui addestrare l’HMM.
Per analizzare il regime di mercato con i modelli di Markov nascosti per l’indice S%P500 dobbiamo prevedere due distinte attività di modellazione. Nella prima adattiamo l’HMM a due stati di regime ai rendimenti dell’S&P500, mentre nella seconda utilizziamo tre stati. Successivamente confrontiamo i risultati ottenuti con i due modelli.
In questo esempio seguiamo un approccio simile a quello adottato con i dati simulati per applicare il modello Hidden Markov. Tuttavia, invece di generare rendimenti da due distribuzioni gaussiane, scarichiamo i dati storici reali sfruttando la libreria yfinance:
data = yfinance.download("^GSPC", start="2004-01-01", end="2017-11-01", group_by='ticker', auto_adjust=False)
data = data["^GSPC"]
data = data.asfreq('b').fillna(method='ffill')
Return = data['Adj Close'].pct_change()
LogRet = np.log(data['Adj Close']).diff().dropna()
plt.plot(LogRet)
plt.show()
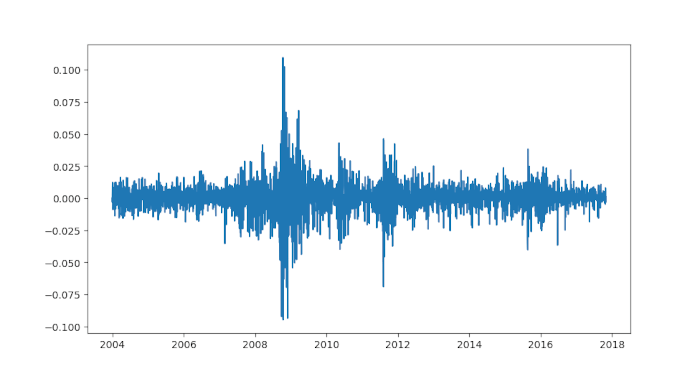
from hmmlearn.hmm import GaussianHMM
import matplotlib
matplotlib.use('TkAgg') # o 'Qt5Agg' se disponibile
rets = np.column_stack([LogRet])
# Create the Gaussian Hidden markov Model and fit it to the returns data
hmm_model = GaussianHMM(
n_components=2, covariance_type="full", n_iter=1000
).fit(rets)
post_prob = hmm_model.predict_proba(rets)
# Creiamo il grafico con dimensioni esplicite
fig, axs = plt.subplots(2, figsize=(12, 6), sharex=True)
axs[0].plot(rets, color='blue')
axs[0].set_ylabel('Returns')
axs[1].plot(post_prob, label=['Regime 1', 'Regime 2'])
axs[1].set_ylabel('Probability')
axs[1].legend(loc='upper right')
plt.tight_layout()
plt.show()
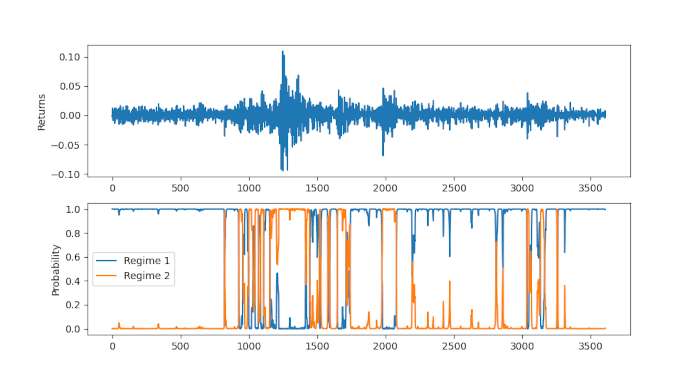
Identificazione dei regimi
Possiamo vedere che dal 2004 al 2007 i mercati erano più calmi e quindi il modello Hidden Markov ha dato un’elevata probabilità a posteriori di regime n. 1 per questo periodo. Tuttavia, tra il 2007 e il 2009 i mercati sono stati incredibilmente volatili a causa della crisi dei mutui subprime. Questo causa inizialmente un rapido cambio delle probabilità a posteriori tra i due stati, ma resta comunque abbastanza coerentemente nel regime n. 2 durante tutto il 2008.
I mercati sono diventati più calmi nel 2010, ma nel 2011 si è verificata un’ulteriore volatilità, portando ancora una volta l’HMM a dare un’elevata probabilità a posteriori per il regime 2. Dopo il 2011 i mercati sono tornati a calmarsi e l’HMM restituisce costantemente alte probabilità per il regime 1. Nel 2015 i mercati sono diventati ancora una volta più instabili e ciò si riflette nell’HMM con una maggiore frequenza di passaggi da un regime all’altro.
Modello a 3 stati
Lo stesso processo verrà ora eseguito per un HMM a tre stati. ci sono poche modifiche da fare nel codice, ad eccezione della modifica del parametro n_components=3 e della della legenda del grafico:
# Create the Gaussian Hidden markov Model and fit it to the returns data
hmm_model = GaussianHMM(
n_components=3, covariance_type="full", n_iter=1000
).fit(rets)
post_prob = hmm_model.predict_proba(rets, None)
# Creiamo il grafico con dimensioni esplicite
fig, axs = plt.subplots(2, figsize=(12, 6), sharex=True)
axs[0].plot(rets, color='blue')
axs[0].set_ylabel('Returns')
axs[1].plot(post_prob, label=['Regime 1', 'Regime 2','Regime 3'])
axs[1].set_ylabel('Probability')
axs[1].legend(loc='upper right')
plt.tight_layout()
plt.show()
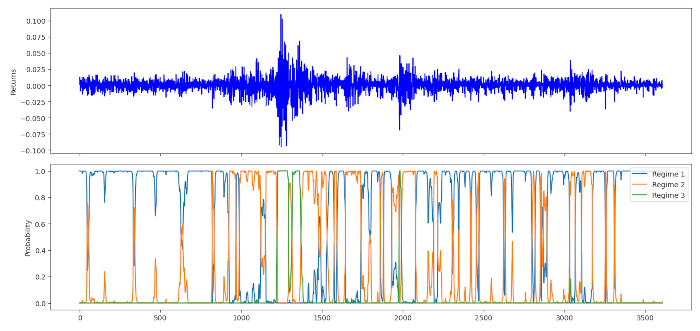
La lunghezza dei dati rende il grafico delle probabilità a posteriori un po’ più complicato da interpretare. Dato che il modello è costretto a considerare tre regimi separati, otteniamo a un comportamento di frequente passaggio tra il Regime #1 e il Regime #2 nel periodo più calmo dal 2004 al 2007. Tuttavia, nei periodi volatili del 2008, 2010 e 2011, il regime n. 3 domina la probabilità a posteriori indicando uno stato altamente volatile. Dopo il 2011 il modello torna al passaggio tra il Regime #1 e il Regime #2.
È chiaro che la scelta del numero iniziale di stati da applicare a un flusso di rendimenti reali è un elemento critico. Dipende dalla tipologia di asset utilizzata, da come viene eseguita la negoziazione di questo asset e dal periodo temporale considerato.
Conclusione
Abbiamo descritto le prime applicazioni per determinare il regime di mercato con i modelli di markov nascosti. Un’applicazione interessante consiste nell’utilizzare il modello di Markov nascosto in una sottoclasse di RiskManager nel motore di backtesting e trading live di un sistema di trading automatico. In questo modo possiamo determinare quando applicare una strategia trend following nel tentativo di migliorare la redditività in caso di assenza di gestione del rischio.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“