In questa lezione esploriamo il test di Dickey Fuller Aumentato per serie cointegrate CADF. La procedura Cointegrated Augmented Dickey-Fuller (CADF) estende il test ADF includendo il parametro di regressione \(\beta\) – l’hedge ratio – fondamentale per costruire la combinazione lineare tra due serie temporali. Abbiamo già introdotto il CADF nel contesto della modellazione statistica.
Nella precedente lezione sulla cointegrazione abbiamo simulato due serie temporali non stazionarie che formano una coppia cointegrata per una combinazione lineare specifica. Abbiamo applicato i test statistici Augmented Dickey-Fuller, Phillips-Perron e Phillips-Ouliaris per identificare radici unitarie e cointegrazione.
Con il CADF identifichiamo il coefficiente di regressione \(\beta\) per le due serie, ma non possiamo stabilire in automatico quale serie usare come variabile dipendente o indipendente. In termini di machine learning statistico, ci chiediamo come prevedere la risposta \(Y\) dalla caratteristica \(X\). Per risolvere questo dubbio, calcoliamo la statistica ADF di entrambe le regressioni e scegliamo quella che genera una serie stazionaria.
Test di Dickey Fuller aumentato e cointegrato
Con il test di Dickey Fuller aumentato e cointegrato CADF vogliamo determinare un rapporto di copertura (hedge-ratio) ottimale tra due serie da usare nel trading mean-reverting. Questo approccio risolve un problema già evidenziato nella lezione precedente. In particolare, definiamo il rapporto long-short per ciascuna coppia nel pairs trading.
Il CADF segue una procedura semplice. Prendiamo i dati storici dei due asset, eseguiamo una regressione lineare e calcoliamo i coefficienti di regressione \(\alpha\) e \(\beta\), che indicano intercetta e pendenza. La pendenza ci rivela la quantità relativa da scambiare per ogni asset nella coppia.
Una volta ottenuto il coefficiente di pendenza – cioè il rapporto di copertura – eseguiamo un test di Dickey Fuller aumentato ADF (come nella lezione precedente) sui residui della regressione. In questo modo verifichiamo la stazionarietà e quindi la presenza di cointegrazione.
Usiamo Python per eseguire la procedura CADF, sfruttando le librerie arch, statsmodels e yfinance per il test ADF e l’acquisizione dei dati storici.
Iniziamo costruendo un set di dati sintetici con proprietà note di cointegrazione, per verificare se la procedura CADF riesce a rilevare stazionarietà e rapporto di copertura. Applichiamo poi lo stesso metodo a dati storici reali, in preparazione all’implementazione di strategie di trading mean-reverting.
CADF sui dati simulati
Descriviamo il metodo CADF utilizzando dati simulati. Riprendiamo le stesse serie temporali generate nella lezione precedente.
Ricordiamo di aver costruito artificialmente due serie temporali non stazionarie che producono una serie residua stazionaria per una combinazione lineare specifica.
Utilizziamo la funzione OLS della libreria statsmodels per eseguire la regressione lineare tra le due serie. In questo modo otteniamo una stima dei coefficienti di regressione e quindi il miglior rapporto di copertura.
Cominciamo importando le librerie necessarie per condurre il test Dickey Fuller aumentato ADF:
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
Impostiamo il seed per il generatore di numeri casuali e creiamo una serie storica stocastica a partire da una random walk sottostante, \(z_t\). Quindi creiamo due serie che rinominiamo \(p_t\) e \(q_t\) in modo da non confonderci i nomi originali \(x_t\) e \(y_t\) con i nomi convenzionali per le regressioni delle risposte e dei predittori:
np.random.seed(123)
n = 1000
z = np.zeros(n)
for i in range(1, n):
z[i] = z[i-1] + np.random.standard_normal(1)
p = 0.3 * z + np.random.standard_normal(1000)
q = 0.6 * z + np.random.standard_normal(1000)
OLS, che calcola una regressione lineare tra due vettori. In questo caso impostiamo \(q_t\) come variabile indipendente e \(p_t\) come variabile dipendente:
q_const = sm.add_constant(q)
comb = sm.OLS(p, q_const)
model = comb.fit()
print(model.summary())
Se diamo un’occhiata al modello di regressione lineare, possiamo vedere che la stima per il coefficiente di regressione \(\beta\) è di circa 0,5. Questo valore è accettabile dato che \(q_t\) dipende due volte da \(z_t\) rispetto a \(\)p_t[/latex (0,6 rispetto a 0,3):
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.909
Model: OLS Adj. R-squared: 0.909
Method: Least Squares F-statistic: 9924.
Date: Prob (F-statistic): 0.00
Time: 16:54:09 Log-Likelihood: -1489.2
No. Observations: 1000 AIC: 2982.
Df Residuals: 998 BIC: 2992.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.1331 0.046 -2.871 0.004 -0.224 -0.042
x1 0.4795 0.005 99.620 0.000 0.470 0.489
==============================================================================
Omnibus: 1.077 Durbin-Watson: 2.003
Prob(Omnibus): 0.584 Jarque-Bera (JB): 0.952
Skew: -0.029 Prob(JB): 0.621
Kurtosis: 3.140 Cond. No. 13.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Infine, applichiamo il test Dickey Fuller aumentato ADF ai residui del modello lineare per verificare la stazionarietà:
from arch.unitroot import ADF
resid = model.resid
adf = ADF(resid)
print(adf.summary())
La statistica del test di Dickey Fuller aumentato è molto bassa, fornendoci un P-value molto piccolo. Possiamo probabilmente rifiutare l’ipotesi nulla della presenza di una radice unitaria e concludere che abbiamo una serie stazionaria e quindi una coppia cointegrata. Questo chiaramente conferma la bontà dei dati che abbiamo simulato per avere queste proprietà.
Augmented Dickey-Fuller Results
=====================================
Test Statistic -20.356
P-value 0.000
Lags 2
-------------------------------------
Trend: Constant
Critical Values: -3.44 (1%), -2.86 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
Vediamo ora come applicare la procedura CADF a diversi set di dati finanziari storici.
CADF applicato ai dati finanziari
Esistono molti modi per creare un set di asset cointegrati. Un approccio comune consiste nell’utilizzare ETF con caratteristiche simili. Un buon esempio riguarda un ETF che rappresenta un paniere di società estrattive dell’oro, abbinato a un ETF che segue il prezzo spot dell’oro. Allo stesso modo possiamo usare il petrolio greggio o altre commodity simili.
In alternativa possiamo costruire coppie più strette considerando classi di azioni differenti dello stesso titolo, come accade nel caso della Royal Dutch Shell mostrato nell’esempio seguente. Un altro esempio interessante riguarda la famosa holding Berkshire Hathaway, guidata da Warren Buffet e Charlie Munger, che presenta azioni di classe A e B. In questo caso però dobbiamo prestare attenzione e verificare se possiamo creare una strategia di mean-reverting redditizia sulla coppia, a seconda della forza della cointegrazione.
EWA e EWC
Nel mondo quantitativo un esempio celebre di test di Dickey Fuller aumentato per serie cointegrate (CADF) applicato a dati azionari proviene dal lavoro di Ernie Chan[1]. Analizziamo una coppia cointegrata formata da due ETF con i ticker EWA ed EWC, che rappresentano panieri di titoli australiani e canadesi. Poiché entrambi i paesi basano fortemente l’economia sulle materie prime, è probabile che questi ETF condividano una tendenza stocastica simile.
Ernie utilizza MatLab per le sue analisi, ma in questa lezione lavoriamo con Python. Per rendere l’esempio più utile, abbiamo deciso di usare lo stesso intervallo temporale del suo studio, così da confrontare direttamente i risultati.
Come primo passo importiamo la libreria yfinance, che ci permette di scaricare dati finanziari da Yahoo Finance. Poi otteniamo i prezzi di chiusura aggiustati per EWA ed EWC, utilizzando lo stesso periodo scelto da Ernie: dal 26 aprile 2006 al 9 aprile 2012.
import yfinance as yf
EWA = yf.download('EWA', start="2006-04-26", end="2012-04-09", group_by='ticker', auto_adjust=False)
EWA = EWA['EWA']
EWC = yf.download('EWC', start="2006-04-26", end="2012-04-09", group_by='ticker', auto_adjust=False)
EWC = EWC['EWC']
ewa = EWA['Adj Close']
ewc = EWC['Adj Close']
Per completezza replichiamo i grafici del lavoro di Ernie, in modo che da vedere lo stesso codice nell’ambiente Python. In primo luogo, tracciamo i prezzi degli stessi ETF.
import matplotlib.pyplot as plt
plt.plot(ewa.values, color="blue")
plt.plot(ewc.values, color="red")
plt.show()
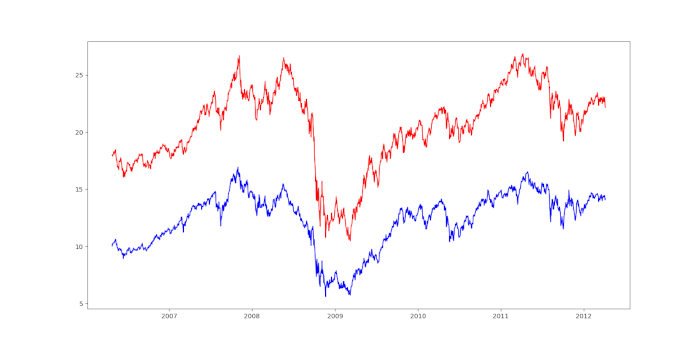
Possiamo notare che differisce leggermente dal grafico riportato nel lavoro di Ernie dato che in stiamo usando i prezzi rettificati, invece dei prezzi di chiusura non rettificati.
Possiamo anche creare un grafico a dispersione dei prezzi:
plt.scatter(ewa, ewc)
plt.show()
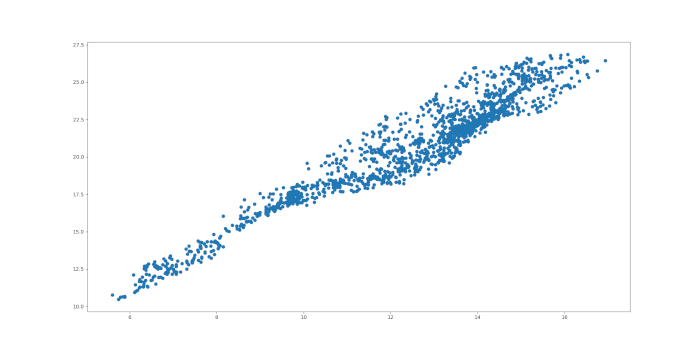
A questo punto dobbiamo eseguire le regressioni lineari tra le due serie di prezzi. Tuttavia, come detto in precedenza, non è chiaro quale delle due serie sia la variabile dipendente e quale quella indipendente. Proveremo entrambe le possibilità e faremo una scelta basata sulla negatività della statistica del test di Dickey Fuller aumentato ADF.
Applicazione del CADF
Usiamo la funzione del modello lineare OLS per la valutare la regressione. In questo modo otteniamo l’intercetta e il coefficiente di regressione per queste coppie.
import statsmodels.api as sm
comb1 = sm.OLS(EWC_adjcls, sm.add_constant(EWA_adjcls)).fit()
comb2 = sm.OLS(EWA_adjcls, sm.add_constant(EWC_adjcls)).fit()
print(comb1.summary())
print(comb2.summary())
Possiamo tracciare i residui e valutare visivamente la stazionarietà della serie:
resid1 = comb1.resid
plt.plot(resid1)
plt.show()
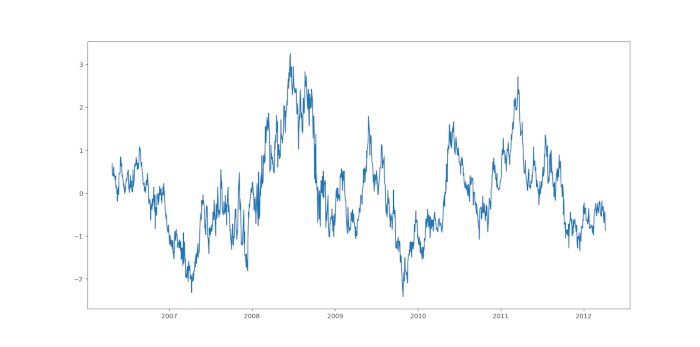
Vediamo il report della regressione lineare con EWA come variabile indipendente:
print(comb1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Adj Close R-squared: 0.921
Model: OLS Adj. R-squared: 0.921
Method: Least Squares F-statistic: 1.742e+04
Date: Prob (F-statistic): 0.00
Time: 09:41:08 Log-Likelihood: -2043.8
No. Observations: 1499 AIC: 4092.
Df Residuals: 1497 BIC: 4102.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 3.1346 0.125 25.146 0.000 2.890 3.379
Adj Close 1.4385 0.011 132.001 0.000 1.417 1.460
==============================================================================
Omnibus: 59.330 Durbin-Watson: 0.049
Prob(Omnibus): 0.000 Jarque-Bera (JB): 65.562
Skew: 0.509 Prob(JB): 5.80e-15
Kurtosis: 3.116 Cond. No. 58.7
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Vediamo che il modello restituisce un’intercetta \(\alpha=3.1346\) e un coefficiente \(\beta=1.4385\).
Allo stesso modo, vediamo di seguito il report per EWC come variabile indipendente:
print(comb2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Adj Close R-squared: 0.921
Model: OLS Adj. R-squared: 0.921
Method: Least Squares F-statistic: 1.742e+04
Date: Prob (F-statistic): 0.00
Time: 09:41:12 Log-Likelihood: -1437.0
No. Observations: 1499 AIC: 2878.
Df Residuals: 1497 BIC: 2889.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -1.1192 0.095 -11.798 0.000 -1.305 -0.933
Adj Close 0.6402 0.005 132.001 0.000 0.631 0.650
==============================================================================
Omnibus: 24.924 Durbin-Watson: 0.051
Prob(Omnibus): 0.000 Jarque-Bera (JB): 23.921
Skew: -0.274 Prob(JB): 6.39e-06
Kurtosis: 2.714 Cond. No. 114.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In questo caso il modello restituisce un’intercetta\(\alpha=-1.1192\) e un coefficiente \(\beta=0.6402\).
I risultati ottenuti presentano una criticità. Possiamo notare una notevole differenza tra i valori dei coefficienti di regressione dei due modelli. Dobbiamo quindi utilizzare la statistica del test di Dickey Fuller aumentato ADF per determinare il rapporto di copertura (hedge-ratio) ottimale.
Per EWA come variabile indipendente otteniamo:
from arch.unitroot import ADF
adf1 = ADF(comb1.resid, lags=1)
print(adf1.summary())
Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.650
P-value 0.005
Lags 1
-------------------------------------
Trend: Constant
Critical Values: -3.43 (1%), -2.86 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
La statistica del test restituisce un p-value inferiore a 0,05 fornendo la prova che possiamo rifiutare l’ipotesi nulla di una radice unitaria al livello del 5%.
Allo stesso modo per EWC come variabile indipendente ottienamo:
adf2 = ADF(comb2.resid, lags=1)
print(adf2.summary())
Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.655
P-value 0.005
Lags 1
-------------------------------------
Trend: Constant
Critical Values: -3.43 (1%), -2.86 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
Ancora una volta, raccogliamo prove sufficienti per rifiutare l’ipotesi nulla sulla presenza di una radice unitaria, il che ci indica una serie stazionaria e quindi una coppia cointegrata al livello del 5%.
Osserviamo che la statistica del test di Dickey Fuller aumentato per EWC, quando la usiamo come variabile indipendente, risulta leggermente più piccola (più negativa) rispetto a quella ottenuta con EWA. Per questo motivo, scegliamo EWC come combinazione lineare per ogni futura applicazione di trading.
Conclusioni
In questa lezione applichiamo il CADF per ottenere il rapporto di copertura ottimale tra due serie temporali cointegrate. Nelle prossime lezioni descriviamo il test di Johansen, uno strumento utile per costruire serie temporali cointegrate con più di due asset, ampliando così il nostro universo di trading e le possibilità strategiche.
Analizziamo anche il fatto che il rapporto di copertura non si mantiene stazionario nel tempo, e adottiamo tecniche per aggiornarlo in presenza di nuove informazioni. A tal fine, utilizziamo l’approccio bayesiano tramite il filtro di Kalman.
Dopo aver esplorato questi test, li integriamo in diverse strategie di trading già disponibili per valutarne le prestazioni considerando costi di transazione realistici.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“

