In questa lezione presentiamo il test di Johansen [2] che ci consente di verificare se tre o più serie temporali sono cointegrate. Calcoliamo così una serie stazionaria ottenuta da una combinazione lineare delle serie sottostanti. Useremo questa procedura nelle lezioni successive per costruire un portafoglio di asset mean-reverting da utilizzare nel trading.
Nella precedente lezione sul test CADF (Cointegrated Augmented Dickey Fuller) abbiamo evidenziato che uno dei principali limiti del test riguarda l’applicazione esclusiva a due serie temporali distinte. Tuttavia, possiamo facilmente immaginare un insieme di tre o più attività finanziarie che condividono una relazione cointegrata sottostante.
Un esempio semplice riguarda tre classi di azioni distinte sullo stesso asset, mentre un caso più interessante considera tre ETF diversi che replicano specifiche aree delle azioni delle materie prime insieme ai prezzi spot delle materie prime sottostanti.
Partiamo dalla teoria alla base del test di Johansen e poi applichiamo la procedura su dati simulati con proprietà di cointegrazione note a priori. Infine, testiamo il metodo su dati finanziari storici per scoprire se riusciamo a identificare un portafoglio di asset cointegrati.
Test di Johannsen
In questa sezione introduciamo i concetti matematici che stanno alla base del test di Johansen, utile per analizzare se due o più serie temporali possano formare una relazione di cointegrazione. Nel trading quantitativo, questo ci permette di costruire portafogli composti da due o più titoli da usare in strategie di trading mean-reverting.
I dettagli teorici del test di Johansen richiedono familiarità con le serie temporali multivariate. In particolare, consideriamo i Modelli Autoregressivi Vettoriali (VAR) — non da confondere con il Value at Risk (VaR) — che estendono multidimensionalmente i Modelli Autoregressivi già trattati.
Un modello autoregressivo vettoriale generale somiglia al modello AR(p), con la differenza che ogni elemento è un vettore di variabili e i coefficienti sono matrici. La forma generale del modello VAR(p) è:
\(\begin{eqnarray}{\bf x_t} = {\bf \mu} + A_1 {\bf x_{t-1}} + \ldots + A_p {\bf x_{t-p}} + {\bf w_t}\end{eqnarray}\)
Dove \({\bf \mu}\) rappresenta il vettore delle intercette delle serie, \(A_i\) sono le matrici dei coefficienti per ogni lag e \({\bf w_t}\) indica un termine di rumore gaussiano multivariato con media zero.
Passiamo quindi a definire un modello di correzione degli errori vettoriale (VECM) differenziando le serie:
\(\begin{eqnarray}\Delta {\bf x_t} = {\bf \mu} + A {\bf x_{t-1}} + \Gamma_1 \Delta {\bf x_{t-1}} + \ldots + \Gamma_p \Delta {\bf x_{t-p}} + {\bf w_t}\end{eqnarray}\)
dove \(\Delta {\bf x_t} := {\bf x_t} – {\bf x_{t-1}}\) è l’operatore differenziale, \(A\) è la matrice dei coefficienti per il primo lag e \(\Gamma_i\) rappresentano le matrici per ogni lag differenziato.
Il test verifica se la matrice A sia nulla, condizione che indica assenza di cointegrazione.
Applicazione del test
Il test di Johansen risulta più flessibile rispetto alla procedura CADF descritta nella lezione precedente, perché identifica più combinazioni lineari di serie temporali per costruire portafogli stazionari. Per farlo, eseguiamo la decomposizione in autovalori della matrice A. Il rango di A, indicato con r, viene testato sequenzialmente: da zero a uno, fino a \(r=n-1\), dove n è il numero di serie temporali analizzate.
L’ipotesi nulla di \(r=0\) indica assenza di cointegrazione, mentre un rango \(r > 0\) implica la presenza di una relazione di cointegrazione tra due o più serie temporali.
La decomposizione degli autovalori genera un insieme di autovettori. Le componenti dell’autovettore corrispondente all’autovalore maggiore rappresentano i candidati a formare i coefficienti di una combinazione lineare delle serie, creando così un portafoglio stazionario. Questo approccio differisce dal test CADF (procedura di Engle-Granger), che richiede di determinare a priori la combinazione lineare tramite regressione lineare e minimi quadrati ordinari (OLS).
Nel test di Johansen stimiamo i coefficienti della combinazione lineare direttamente durante il test. Questo comporta una minore potenza statistica rispetto al CADF, e potremmo incontrare casi in cui il test non rifiuta l’ipotesi nulla di mancata cointegrazione, nonostante il CADF suggerisca il contrario. Approfondiremo questi casi più avanti.
Il modo più efficace per comprendere il test di Johansen è applicarlo su dati finanziari simulati e storici.
Test di Johansen su dati simulati
Ora che abbiamo descritto le basi teoriche del test, lo applichiamo utilizzando Python. In particolare utilizziamo la libreria statsmodels, che implementa il test di Johansen con la funzione coint_johansen.
Il primo compito è importare le librerie necessarie. Impostiamo il seed in modo che i risultati del generatore di numeri casuali possano essere replicati, quindi creiamo la passeggiata casuale sottostante \(z_t\). Infine creiamo le tre serie temporali che condividono la stessa passeggiata casuale sottostante. Sono indicati rispettivamente come \(p_t\), \(q_t\) e \(r_t\):
import numpy as np
import pandas as pd
from statsmodels.tsa.vector_ar.vecm import coint_johansen
np.random.seed(123)
z = np.zeros(10000)
for i in range(1, 10000):
z[i] = z[i-1] + np.random.normal()
p = 0.3 * z + np.random.normal(size=10000)
q = 0.6 * z + np.random.normal(size=10000)
r = 0.2 * z + np.random.normal(size=10000)
Applichiamo poi la funzione coint_johansen a un DataFrame contenente tutte e tre le serie temporali.
Il parametro det_order indica se includere un termine costante o di drift nel modello,
mentre k_ar_diff è il numero di ritardi da usare nel modello VAR, e lo impostiamo al minimo, k_ar_diff = 2.
Infine, specifichiamo l’opzione del test da utilizzare: “trace” oppure “maxeig” (massimo autovalore); in questo caso usiamo "trace".
data = pd.DataFrame({'p': p, 'q': q, 'r': r})
jotest = coint_johansen(data, det_order=-1, k_ar_diff=2)
# Stampa dei risultati
print("######################")
print("# Procedura Johansen #")
print("######################")
print("Tipo di test: statistica trace, senza termine costante")
print("Autovalori (lambda):")
print(jotest.eig)
print("\nValori della statistica di test e valori critici:")
for idx, label in enumerate([0,1,2]):
stat = jotest.lr1[idx]
crit = jotest.cvt[idx] # [10%, 5%, 1%]
print(f"H0: r <= {label} | test = {stat:.2f}, 10% = {crit[0]:.2f}, 5% = {crit[1]:.2f}, 1% = {crit[2]:.2f}")
print("\nAutovettori normalizzati (relazioni di cointegrazione):")
print(pd.DataFrame(jotest.evec, columns=['p.l2', 'q.l2', 'r.l2']))
print("\nPesi W (matrice di caricamento):")
print(pd.DataFrame(jotest.eig, columns=["W"]))
######################
# Procedura Johansen #
######################
Tipo di test: statistica trace, senza termine costante
Autovalori (lambda):
[2.55672110e-01 2.51190742e-01 7.45197062e-06]
Valori della statistica di test e valori critici:
H0: r <= 0 | test = 5843.77, 10% = 21.78, 5% = 24.28, 1% = 29.51
H0: r <= 1 | test = 2891.92, 10% = 10.47, 5% = 12.32, 1% = 16.36
H0: r <= 2 | test = 0.07, 10% = 2.98, 5% = 4.13, 1% = 6.94
Autovettori normalizzati (relazioni di cointegrazione):
p.l2 q.l2 r.l2
0 0.121041 -1.519024 -0.007592
1 -0.598822 0.633084 -0.015871
2 1.614455 0.378220 -0.006179
Pesi W (matrice di caricamento):
W
0 0.255672
1 0.251191
2 0.000007
Risultati del test
Proviamo ad interpretare tutte queste informazioni! La prima sezione mostra la statistica del test ‘trace’ per le tre ipotesi \(r=0\), \(r \leq 1\) e \(r \leq 2\). Per ognuno di questi tre test abbiamo non solo la statistica stessa ma anche i valori critici a determinati livelli di confidenza: rispettivamente 10%, 5% e 1%.
La prima ipotesi,\(r = 0\), verifica la presenza di cointegrazione. Poiché la statistica del test supera significativamente il livello dell’1% (5843,77>29.51) abbiamo forti prove per rifiutare l’ipotesi nulla di mancata cointegrazione. La seconda prova per \(r \leq 1\) contro l’ipotesi alternativa \(r \gt 1\) fornisce anch’essa prove chiare per rifiutare \(r \leq 1\) poiché la statistica del test supera significativamente il livello dell’1%. Anche la prova finale per \(r \leq 2\) contro \(r \gt 2\) fornisce prove sufficienti per rifiutare l’ipotesi nulla che \(r \leq 2\) e quindi si può concludere che il rango della matrice è maggiore di 2.
Possiamo dunque concludere che il rango della matrice è \(r=3\), il che ci dice che è necessaria una combinazione lineare delle tre serie temporali per ottenere una serie stazionaria. Questo risultato è atteso, dato che la componente sottostante comune a tutte le serie è un random walk non stazionario.
Come procediamo per formare una tale combinazione lineare? La risposta è utilizzare le componenti del vettore proprio associate al più grande autovalore.
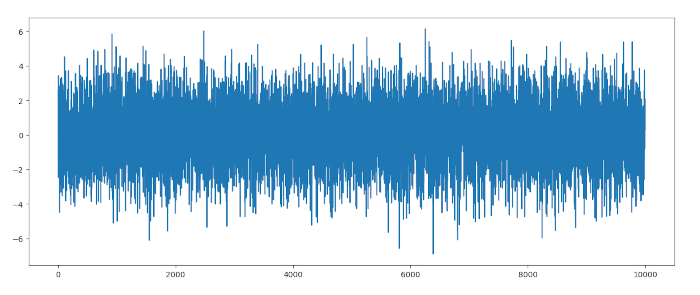
In precedenza abbiamo menzionato che il più grande autovalore è approssimativamente 0.256. Esso corrisponde al vettore indicato nella colonna p.l2, ed è circa pari a (0.121, -0,598, 1.614). Se formiamo una combinazione lineare delle serie usando queste componenti, otteniamo una serie stazionaria:
import matplotlib.pyplot as plt
# Supponendo che p, q e r siano array o pandas Series già definiti
s = 0.121041 * p - 0.598822 * q + 1.614455 * r
plt.plot(s)
plt.show()
from arch.unitroot import *
adf = ADF(s)
print(adf.summary())
Augmented Dickey-Fuller Results
=====================================
Test Statistic -99.274
P-value 0.000
Lags 0
-------------------------------------
Trend: Constant
Critical Values: -3.43 (1%), -2.86 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
La statistica del test di Dickey-Fuller è molto bassa, dato che abbiamo un p-value basso. Quindi possiamo rifiutare l’ipotesi nulla di una radice unitaria e abbiamo la prova di una serie stazionaria formata da una combinazione lineare.
Questo non dovrebbe sorprenderci in quanto, per costruzione, l’insieme di serie è stato progettato per formare una combinazione lineare stazionaria. Tuttavia, è istruttivo seguire i test su dati simulati poiché ci aiuta nell’analisi dei dati finanziari reali, come nel prossimo capitolo.
Test di Johansen sui dati finanziari
In questa sezione esamineremo due serie separate di panieri di ETF: EWA, EWC e IGE, nonché SPY, IVV e VOO.
EWA, EWC e IGE
Nella precedente lezione abbiamo esaminato il lavoro di Ernest Chan [1] sulla cointegrazione tra i due ETF di EWA ed EWC, che rappresentano panieri di azioni rispettivamente per le economie australiana e canadese.
Chan descrive anche il test di Johansen come mezzo per aggiungere un terzo ETF al mix, ovvero l’IGE, che contiene un paniere di stock di risorse naturali. L’idea di base è che questi ETF dovrebbero subire l’influenza delle tendenze stocastiche delle merci e quindi possono formare una relazione di cointegrazione.
Nel suo lavoro, Chan ha eseguito la procedura di Johansen utilizzando MatLab e ha potuto respingere l’ipotesi \(r \leq 2\) al livello del 5%. Questo implica che ha trovato prove a sostegno dell’esistenza di una combinazione lineare stazionaria di EWA, CAE e IGE.
Sarebbe utile vedere se possiamo replicare i risultati usando Python. Iniziamo utilizzando la libreria yfinance per scaricare i dati storici delle serie finanziare e quindi effettuare il test di Johansen con la libreria statsmodels.
import yfinance as yf
import pandas as pd
from statsmodels.tsa.vector_ar.vecm import coint_johansen
EWA = yf.download('EWA', start="2006-04-26", end="2012-04-09", group_by='ticker', auto_adjust=False)
EWA = EWA['EWA']
EWC = yf.download('EWC', start="2006-04-26", end="2012-04-09", group_by='ticker', auto_adjust=False)
EWC = EWC['EWC']
IGE = yf.download('IGE', start="2006-04-26", end="2012-04-09", group_by='ticker', auto_adjust=False)
IGE = IGE['IGE']
df = pd.DataFrame({'EWA': EWA['Adj Close'], 'EWC': EWC['Adj Close'], 'IGE': IGE['Adj Close']})
jotest = coint_johansen(df, 0, 1)
######################
# Procedura Johansen #
######################
Tipo di test: statistica trace, senza termine costante
Autovalori (lambda):
[0.01182274 0.00827971 0.00292614]
Valori della statistica di test e valori critici:
H0: r <= 0 | test = 34.64, 10% = 27.07, 5% = 29.80, 1% = 35.46
H0: r <= 1 | test = 16.83, 10% = 13.43, 5% = 15.49, 1% = 19.93
H0: r <= 2 | test = 4.39, 10% = 2.71, 5% = 3.84, 1% = 6.63
Autovettori normalizzati (relazioni di cointegrazione):
p.l2 q.l2 r.l2
0 1.630212 -0.262338 0.124490
1 -1.512728 -0.718877 0.415965
2 0.355005 0.739899 -0.159698
Pesi W (matrice di caricamento):
W
0 0.011823
1 0.008280
2 0.002926
Risultati del test
Forse la prima cosa che si nota è la differenza tra i valori della statistica Trace del nostro test e quelli forniti nel pacchetto MatLab utilizzato da Chan.
La statistica Trace del nostro test è sostanzialmente simile per \(r \leq 2\) a 4,39 contro 4,471 dei risultati di Chan, mentre i valori critici sono molto simili. Fondamentalmente, la statistica Trace del test è maggiore rispetto al livello del 5%, quindi possiamo concludere che dovremmo avere tre relazioni di cointegrazione con una certezza del 95%.
Da sottolineare che non c’è differenza tra i due insiemi di serie temporali utilizzati per ciascuna analisi! L’unica differenza risiede nell’implementazioni del test di Johansen, che sono diverse tra MatLab e Python. Ciò significa che dobbiamo essere estremamente attenti quando valutiamo i risultati dei test statistici, in particolare tra diverse implementazioni e linguaggi di programmazione.
SPY, IVV e VOO
Un altro approccio consiste nel considerare un paniere di ETF che replicano un indice azionario. Ad esempio, ci sono una moltitudine di ETF che replicano l’indice del mercato azionario statunitense S&P500 come Standard & Poor’s Depository Receipts SPY, iShares IVV e VOO di Vanguard. Dato che replicano tutti lo stesso asset sottostante, è probabile che questi tre ETF abbiano una forte relazione di cointegrazione.
Otteniamo i prezzi di chiusura giornalieri rettificati per ciascuno di questi ETF nell’ultimo anno:
import yfinance as yf
import pandas as pd
from statsmodels.tsa.vector_ar.vecm import coint_johansen
SPY = yf.download('SPY', start="2016-01-01", end="2016-12-31", group_by='ticker', auto_adjust=False)
SPY = SPY['SPY']
IVV = yf.download('IVV', start="2016-01-01", end="2016-12-31", group_by='ticker', auto_adjust=False)
IVV = IVV['IVV']
VOO = yf.download('VOO', start="2016-01-01", end="2016-12-31", group_by='ticker', auto_adjust=False)
VOO = VOO['VOO']
df = pd.DataFrame({'SPY': SPY['Adj Close'], 'IVV': IVV['Adj Close'], 'VOO': VOO['Adj Close']})
jotest = coint_johansen(df, 0, 1)
######################
# Procedura Johansen #
######################
Tipo di test: statistica trace, senza termine costante
Autovalori (lambda):
[0.30282019 0.0384015 0.00288948]
Valori della statistica di test e valori critici:
H0: r <= 0 | test = 100.69, 10% = 27.07, 5% = 29.80, 1% = 35.46
H0: r <= 1 | test = 10.51, 10% = 13.43, 5% = 15.49, 1% = 19.93
H0: r <= 2 | test = 0.72, 10% = 2.71, 5% = 3.84, 1% = 6.63
Autovettori normalizzati (relazioni di cointegrazione):
p.l2 q.l2 r.l2
0 36.640710 -3.711929 1.219376
1 -0.582069 4.525558 -0.335033
2 -39.251692 -0.761318 -1.085090
Pesi W (matrice di caricamento):
W
0 0.302820
1 0.038401
2 0.002889
Eseguiamo in sequenza i test di ipotesi iniziando con l’ipotesi nulla di \(r = 0\) contro l’ipotesi alternativa di \(r \gt 0\). Ci sono prove evidenti per rifiutare l’ipotesi nulla al livello dell’1% e possiamo probabilmente concludere che \(r \gt 0\).
Allo stesso modo verifichiamo l’ipotesi nulla \(r \leq 1\) contro l’ipotesi alternativa \(r \gt 1\). Abbiamo prove sufficienti per rifiutare l’ipotesi nulla al livello dell’1% e possiamo concludere che \(r \gt 1\).
Infine, possiamo rifiuturare l’ipotesi nulla \(r \leq 2\) contro l’ipotesi alternativa \(r \gt 2\) e quindi possiamo concludere che \(r=3\). Ciò significa che possiamo formare una combinazione lineare di tutte e 3 gli asset per un portafoglio di cointegrazione.
Inoltre, dovremmo essere estremamente cauti nell’interpretare questi risultati poiché abbiamo utilizzato solo un anno di dati, ovvero circa 250 giorni di negoziazione. È improbabile che un campione così piccolo fornisca una rappresentazione fedele delle relazioni sottostanti. Quindi bisogna stare sempre attenti nell’interpretare i test statistici!
Conclusioni
Nelle ultime lezioni abbiamo descritto una moltitudine di test statistici per rilevare la stazionarietà tra combinazioni di serie temporali come precursori per creare strategie di trading mean-reverting.
In particolare abbiamo esaminato il test Augmented Dickey-Fuller, Phillips-Perron, Phillips-Ouliaris, Cointegrated Augmented Dickey-Fuller e il test di Johansen.
Siamo ora in grado di applicare questi test a strategie di ritorno verso la media. Possiamo effettuare backtest realistici in Python per queste strategie.
Il codice completo presentato in questa lezione è disponibile nel seguente repository GitHub: “https://github.com/tradingquant-it/TQResearch“