Nelle precedenti lezioni di questo corso abbiamo introdotto la statistica bayesiana, ricavato analiticamente una proporzione binomiale con priori coniugati e descritto le basi della Markov Chain Monte Carlo tramite l’algoritmo Metropolis. In questa lezione introduciamo i modelli di regressione lineare bayesiana ed eseguiamo l’inferenza con la libreria MCMC di PyMC3.
Cominciamo riassumendo l’approccio classico, o frequentista, alla regressione lineare multipla. Proseguiamo con una descrizione dell’approccio bayesiano alla regressione lineare. Infine, introduciamo brevemente il concetto di modello lineare generalizzato (GLM), utile per comprendere la sintassi dei modelli in PyMC3.
Dopo questa panoramica, simuliamo alcuni dati lineari con rumore e utilizziamo PyMC3 per ottenere le distribuzioni a posteriori dei parametri del modello. Usiamo lo stesso procedimento applicato nei modelli di serie temporali come ARMA e GARCH. Questo approccio “simula e adatta” ci consente sia di comprendere meglio il modello, sia di verificare l’accuratezza dell’adattamento confrontandolo con i valori reali dei parametri.
Ora concentriamo l’attenzione sull’approccio frequentista alla regressione lineare.
Regressione lineare frequentista
L’approccio frequentista, o classico, alla regressione lineare multipla considera un modello della forma (Hastie et al [2]):
\(\begin{eqnarray}f \left( \mathbf{X} \right) = \beta_0 + \sum_{j=1}^p \mathbf{X}_j \beta_j + \epsilon = \beta^T \mathbf{X} + \epsilon\end{eqnarray}\)
Qui \(\beta^T\) rappresenta la trasposta del vettore coefficiente \(\beta\) e \(\epsilon \sim \mathcal{N}(0,\sigma^2)\) indica l’errore di misurazione, distribuito normalmente con media zero e deviazione standard \(\sigma\).
In altre parole, il modello \(f(\mathbf{X})\) risulta lineare rispetto ai predittori \(\mathbf{X}\), con l’aggiunta di un errore di misurazione.
Se disponiamo di una serie di dati di allenamento \((x_1, y_1), \ldots, (x_N, y_N)\), puntiamo a stimare i coefficienti \(\beta\) per ottenere il miglior adattamento lineare ai dati. Dal punto di vista geometrico, cerchiamo l’orientamento dell’iperpiano che caratterizza meglio i dati in modo lineare.
In questo contesto, “migliore” significa minimizzare una funzione di errore. Il metodo più diffuso per raggiungere questo obiettivo è quello dei minimi quadrati ordinari (OLS). Consideriamo la somma residua dei quadrati (RSS), cioè la somma dei quadrati delle differenze tra output osservati e stime di regressione lineare:
\(\begin{eqnarray}\text{RSS}(\beta) &=& \sum_{i=1}^{N} (y_i – f(x_i))^2 \\
&=& \sum_{i=1}^{N} (y_i – \beta^T x_i)^2\end{eqnarray}\)
Il metodo OLS mira quindi a minimizzare l’RSS, regolando i coefficienti \(\beta\). La stima di massima verosimiglianza di \(\beta\), che riduce l’RSS al minimo, risulta:
\(\begin{eqnarray}\hat{\beta} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}\end{eqnarray}\)
Per prevedere il valore successivo \(y_{N+1}\) in base ai nuovi dati \(x_{N+1}\), basta moltiplicare i componenti di \(x_{N+1}\) per i relativi coefficienti \(\beta\) e ottenere \(y_{N+1}\).
Vale la pena sottolineare che \(\hat{\beta}\) rappresenta una stima puntuale, ovvero un singolo valore di \(\mathbb{R}^{p+1}\). Nella formulazione bayesiana, questa interpretazione cambia radicalmente.
Modelli di regressione lineare bayesiana
I modelli di regressione lineare bayesiana esprimiamo la regressione lineare in modo probabilistico. Riformuliamo quindi il modello di regressione lineare introducendo le distribuzioni di probabilità. La sintassi assume la seguente forma:
\(\begin{eqnarray}\mathbf{y} \sim \mathcal{N} \left(\beta^T \mathbf{X}, \sigma^2 \mathbf{I} \right)\end{eqnarray}\)
In parole semplici, i valori di risposta \(\mathbf{y}\) derivano da una distribuzione normale multivariata con media uguale al prodotto tra coefficienti \(\beta\) e predittori \(\mathbf{X}\), e varianza pari a \(\sigma^2\). La matrice identità \(\mathbf{I}\) garantisce che la distribuzione sia multivariata.
Questa formulazione si discosta nettamente dall’approccio frequentista. Quest’ultimo non considera distribuzioni di probabilità se non per l’errore di misurazione, mentre il modello bayesiano descrive ogni valore \(y_i\) come campione da una distribuzione normale.
Una domanda naturale che sorge a questo punto è: “Qual è il vantaggio di questa riformulazione?” Possiamo individuare due principali motivi per adottarla (Wiecki [6]):
- Distribuzioni a priori: Se disponiamo di conoscenze preliminari sui parametri, possiamo impostare distribuzioni a priori che le riflettano. In alternativa, possiamo scegliere priori non informativi.
- Distribuzioni a posteriori: Come già osservato, il valore MLE frequentista \(\hat{\beta}\) rappresenta solo una stima puntuale. Invece, il framework bayesiano fornisce un’intera distribuzione di probabilità che caratterizza l’incertezza sui coefficienti \(\beta\). Dopo aver considerato tutti i dati, possiamo quantificare l’incertezza sui parametri \(\hat{\beta}\) attraverso la varianza della distribuzione a posteriori: una varianza più alta implica maggiore incertezza.
Nonostante la concisione della formula bayesiana, essa non offre indicazioni pratiche su come specificare e campionare un modello usando Markov Chain Monte Carlo. Nei prossimi paragrafi vediamo come utilizzare PyMC3 per formulare e sfruttare un modello di regressione lineare bayesiana.
Regressione lineare bayesiana con PyMC3
In questo paragrafo seguiamo un approccio consolidato con esempi statistici: simuliamo alcuni dati con proprietà già note e adattiamo i modelli di regressione lineare bayesiana per verificare la presenza di queste proprietà. Abbiamo già utilizzato questa tecnica in precedenti lezioni, soprattutto nel corso sull’analisi delle serie temporali.
Seguire una tale procedura potrebbe sembrare complicato, ma offre in realtà due principali vantaggi. Il primo consiste nella possibilità di comprendere esattamente come funziona il fitting del modello. Per farlo, dobbiamo prima capirlo, il che ci aiuta a intuire il funzionamento del modello. Il secondo vantaggio consiste nella possibilità di osservare come si comporta il modello (cioè i valori e l’incertezza che restituisce) in una situazione in cui conosciamo i veri valori che stiamo stimando.
In questo approccio con Python usiamo le librerie numpy e pandas per simulare i dati, usiamo seaborn per visualizzare i grafici e infine utilizziamo il modulo Generalized Linear Models (GLM) di PyMC3 per effettuare una regressione lineare bayesiana e campionarla sul nostro set di dati simulati.
Questa analisi si basa principalmente su una raccolta di post di blog scritti da Thomas Wiecki [6] e Jonathan Sedar [5], insieme a basi bayesiane più teoriche di Gelman et al [1].
Cosa sono i modelli lineari generalizzati?
Prima di iniziare a descrivere i modelli di regressione lineare bayesiana, introduciamo brevemente il concetto di modello lineare generalizzato (GLM), utile per formulare il nostro modello in PyMC3.
Un modello lineare generalizzato estende in modo flessibile la regressione lineare ordinaria a forme più generali, come la regressione logistica (classificazione), la regressione di Poisson (per dati discreti) e la stessa regressione lineare.
I GLM permettono alle variabili endogene (le variabili di risposta) di seguire distribuzioni di errore diverse dalla normale (vedi \(\epsilon\) sopra, nel paragrafo della regressione frequentista). Nel modello lineare generalizzato ogni valore della variabile dipendente \(\mathbf{y}\) deriva da una variabile casuale appartenente alla famiglia delle distribuzioni esponenziali. Questa famiglia comprende molte distribuzioni comuni tra cui normale, gamma, beta, chi quadrato, Bernoulli, Poisson e altre.
La media \(\mathbf{\mu}\) di questa distribuzione dipende da \(\mathbf{X}\) secondo la relazione:
\(\begin{eqnarray}\mathbb{E}(\mathbf{y}) = \mu = g^{-1}(\mathbf{X}\beta)\end{eqnarray}\)
dove \(g\) rappresenta la funzione di collegamento. In questo ambito, la varianza si presenta tipicamente come una funzione \(V\) della media:
\(\begin{eqnarray}\text{Var}(\mathbf{y}) = V(\mathbb{E}(\mathbf{y})) = V(g^{-1}(\mathbf{X}\beta))\end{eqnarray}\)
Nell’approccio frequentista, come nella regressione lineare sopra, stimiamo i coefficienti ignoti \(\beta\) attraverso l’approccio di massima verosimiglianza.
Non approfondiamo i GLM perché non costituiscono l’oggetto di questa lezione. Li abbiamo introdotti perché dobbiamo utilizzare il modulo glm di PyMC3, che Thomas Wiecki e altri [6] hanno sviluppato, per specificare facilmente la nostra regressione lineare bayesiana.
Simulazione dei dati e adattamento del modello con PyMC3
Prima di utilizzare PyMC3 per specificare e campionare un modello bayesiano, simuliamo alcuni dati lineari rumorosi. Il seguente codice svolge queste operazioni (modifica ed estende il codice presente nel post di Jonathan Sedar [5]):
Per prima cosa creiamo i valori x, equispaziati in virgola mobile tra 0 e 1, utilizzando np.linspace(). Usiamo poi un modello lineare per simulare i valori y, impostando un’intercetta di 1 e una pendenza di 2. Per creare il set di dati rumoroso aggiungiamo ai valori di y un errore casuale, epsilon, generato con il metodo RandomState.normal() di numpy, che estrae campioni da una distribuzione normale. Impostiamo la media (“loc”) uguale a 0 e la deviazione standard (“scale”) uguale a 0,5.
import bambi as bmb
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns
sns.set(style="darkgrid", palette="muted")
def simulate_linear_data(
start, stop, N, beta_0, beta_1, eps_mean, eps_sigma_sq
):
"""
Simula un dataset random dataset usando il noisy
linear process.
Parameters
----------
N: `int`
Numero dei punti data da simulare
beta_0: `float`
Intercetta
beta_1: `float`
Pendeza del preditore univariato, X
Returns
-------
df: `pd.DataFrame`
Un DataFrame che contiene i valori x e y
"""
# Crea un DataFrame pandas con la colonna 'x' che contiene
# N valori campionati uniformemente tra 0.0 e 1.0
df = pd.DataFrame(
{"x":
np.linspace(start, stop, num=N)
}
)
# Utilizza un modello lineare (y ~ beta_0 + beta_1*x + epsilon)
# per generare una colonna "y" di risposte basate su "x"
df["y"] = beta_0 + beta_1*df["x"] + np.random.RandomState(s).normal(
eps_mean, eps_sigma_sq, N
)
return df
def plot_simulated_data(df):
"""
Tracciare i dati simulati con sns.lmplot().
Parameters
----------
df: `pd.DataFrame`
Un DataFrame che contiene i valori x e y
"""
# Visualizza i dati e la regressione lineare
# frequentista utilizzando il pacchetto seaborn
sns.lmplot(x="x", y="y", data=df, height=10)
plt.xlim(0.0, 1.0)
plt.show()
if __name__ == "__main__":
# Questi sono i nostri parametri "Reali"
beta_0 = 1.0 # Intercept
beta_1 = 2.0 # Slope
# Simula 100 punti dati tra 0 e 1, con una varianza di 0,5
start = 0
stop = 1
N = 100
eps_mean = 0.0
eps_sigma_sq = 0.5
# Random Seed
s = 42
# Simula i dati "lineari" utilizzando i parametri di cui sopra
df = simulate_linear_data(
start, stop, N, beta_0, beta_1, eps_mean, eps_sigma_sq
)
# Visualizza il grafico dei dati simulati
plot_simulated_data(df)
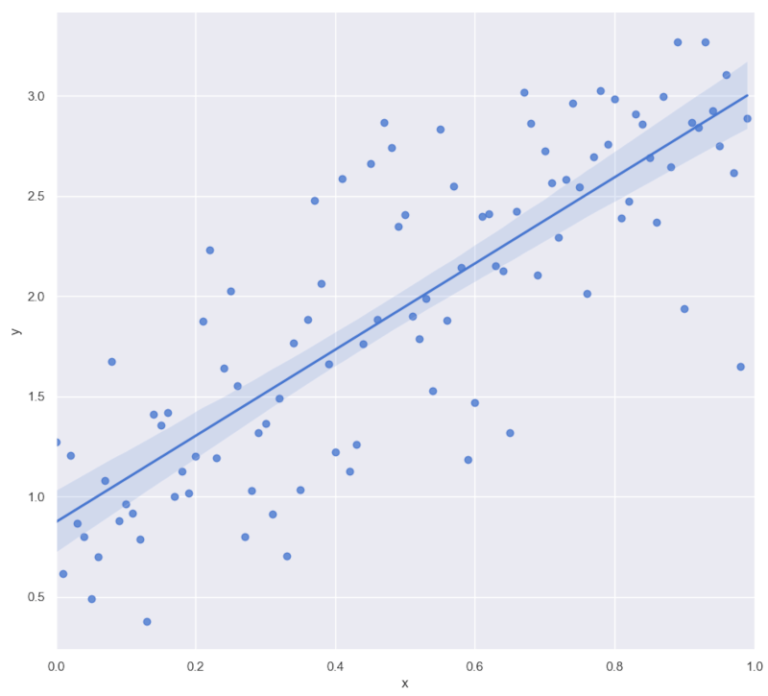
Abbiamo simulato 100 punti dati, impostando un’intercetta \(\beta_0=1\) e una pendenza \(\beta_1=2\). I valori epsilon seguono una distribuzione normale con media zero e varianza \(\sigma^2=\frac{1}{2}\). Abbiamo tracciato i dati usando la funzione sns.lmplot. Inoltre, il metodo adotta un approccio MLE frequentista per adattare una linea di regressione lineare ai dati.
Adattare i modelli di regressione lineare bayesiana
Dopo aver completato la simulazione, procediamo ad adattare una regressione lineare bayesiana sui dati. Qui entra in gioco il modulo glm. Utilizziamo insieme la libreria Bambi, come descritto nel tutorial PyMC. La libreria adotta una sintassi di specifica del modello e genera una matrice di progettazione a partire da una formula lineare. Aggiunge poi variabili casuali per ciascun coefficiente e costruisce un’opportuna verosimiglianza. Se Bambi non è installato, possiamo installarlo tramite il comando pip install bambi.
Infine, utilizziamo il No-U-Turn Sampler (NUTS) per condurre l’inferenza e tracciare il grafico del modello. Consideriamo 5000 campioni dalla distribuzione a posteriori e dedichiamo i primi 500 campioni alla fase di tuning, scartandoli come “burn-in”. PyMC permette di campionare più catene in base al numero di CPU disponibili. Per questa simulazione, impostiamo esplicitamente il numero di core a 1.
import bambi as bmb
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns
sns.set(style="darkgrid", palette="muted")
def simulate_linear_data(
start, stop, N, beta_0, beta_1, eps_mean, eps_sigma_sq
):
"""
Simula un dataset random dataset usando il noisy
linear process.
Parameters
----------
N: `int`
Numero dei punti data da simulare
beta_0: `float`
Intercetta
beta_1: `float`
Pendeza del preditore univariato, X
Returns
-------
df: `pd.DataFrame`
Un DataFrame che contiene i valori x e y
"""
# Crea un DataFrame pandas con la colonna 'x' che contiene
# N valori campionati uniformemente tra 0.0 e 1.0
df = pd.DataFrame(
{"x":
np.linspace(start, stop, num=N)
}
)
# Utilizza un modello lineare (y ~ beta_0 + beta_1*x + epsilon)
# per generare una colonna "y" di risposte basate su "x"
df["y"] = beta_0 + beta_1*df["x"] + np.random.RandomState(s).normal(
eps_mean, eps_sigma_sq, N
)
return df
def plot_simulated_data(df):
"""
Tracciare i dati simulati con sns.lmplot().
Parameters
----------
df: `pd.DataFrame`
Un DataFrame che contiene i valori x e y
"""
# Visualizza i dati e la regressione lineare
# frequentista utilizzando il pacchetto seaborn
sns.lmplot(x="x", y="y", data=df, height=10)
plt.xlim(0.0, 1.0)
plt.show()
if __name__ == "__main__":
# Questi sono i nostri parametri "Reali"
beta_0 = 1.0 # Intercept
beta_1 = 2.0 # Slope
# Simula 100 punti dati tra 0 e 1, con una varianza di 0,5
start = 0
stop = 1
N = 100
eps_mean = 0.0
eps_sigma_sq = 0.5
# Random Seed
s = 42
# Simula i dati "lineari" utilizzando i parametri di cui sopra
df = simulate_linear_data(
start, stop, N, beta_0, beta_1, eps_mean, eps_sigma_sq
)
# Visualizza il grafico dei dati simulati
plot_simulated_data(df)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [Intercept, x, y_sigma]
[-----------------]Sampling 1 chains for 500 tune and 5_000 draw iterations (500 + 5_000 draws total) took 12 seconds.
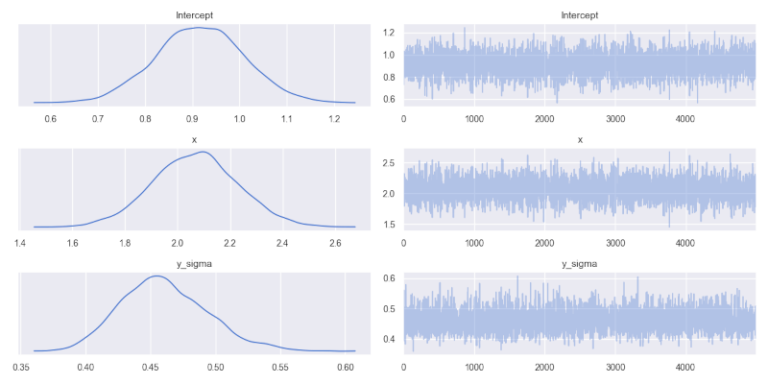
Nella precedente lezione sull’algoritmo Metropolis MCMC abbiamo illustrato le basi dei traceplot. I modelli bayesiani forniscono una distribuzione di probabilità a posteriori completa per ogni parametro del modello, a differenza della stima puntuale dell’approccio frequentista.
Sul lato sinistro del pannello compaiono le distribuzioni marginali di ciascun parametro di interesse. La distribuzione dell’intercetta \(\beta_0\) presenta la sua stima modale/massima a posteriori quasi a 1, vicino al valore reale \(\beta_0=1\). Anche il parametro \(\beta_1\) della pendenza(x) mostra una moda intorno a 2.1, molto prossima al valore reale \(\beta_1=2\). Per il parametro di errore y_sigma, associato al rumore di misurazione del modello, la moda si trova a circa 0.46, leggermente inferiore al valore reale \(\epsilon=0.5\).
In tutti i casi osserviamo una ragionevole varianza associata a ogni marginale a posteriori, indicando un certo grado di incertezza nei valori stimati. Aumentando la quantità di dati simulati ed eseguendo più campionamenti, questa varianza diminuirebbe probabilmente.
Distribuzione di probabili linee di regressione
Il punto chiave da evidenziare è che con i modelli di regressione lineare bayesiana non otteniamo una stima puntuale per la retta di regressione, come avviene nell’approccio frequentista, ma una distribuzione di possibili linee di regressione.
Possiamo tracciare queste linee insieme alla vera linea di regressione e ai dati simulati creati in precedenza. Iniziamo generando la figura, impostando l’asse x come un array di numeri a virgola mobile distribuiti linearmente tra 0 e 1, con 100 intervalli. Tracciamo quindi i dati simulati utilizzando la funzione plt.scatter di Matplotlib e il DataFrame originale, df.
Accediamo ai dati numerici delle distribuzioni posteriori tramite l’oggetto trace generato dal modello. I dati di inferenza della traccia includono i gruppi: posterior, log_likelihood, sample_stats, observed_data. Il gruppo posterior raccoglie i valori dei 5000 campioni delle distribuzioni a posteriori dell’intercetta e della pendenza(x), organizzati in array di forma (1, 5000). Il primo valore indica il numero di catene, il secondo il numero di campioni estratti. Tramite il metodo to_numpy(), possiamo convertire i dati in array numpy. Per ottenere i valori delle intercette in un array pronto all’uso, utilizziamo il comando trace.posterior.Intercept.to_numpy()[0]. Per estrarre i dati delle pendenze, applichiamo un comando analogo, sostituendo ‘Intercept’ con ‘x’, cioè trace.posterior.x.to_numpy()[0]. Così otteniamo due matrici con i valori numerici delle distribuzioni a posteriori di pendenze e intercette.
Il grafico
Per tracciare 100 linee di regressione, selezioniamo casualmente 100 valori dai nostri array. Creiamo un elenco di indici campionati casualmente usando random.randint() di numpy. Poi cicliamo attraverso questi indici, creiamo ogni linea utilizzando l’intercetta e la pendenza corrispondenti, e infine tracciamo le linee sul grafico. Concludiamo tracciando la vera linea di regressione, utilizzando le variabili beta_0 e beta_1 derivate dai dati simulati. Il seguente frammento di codice genera il grafico:
...
def plot_regression_lines(trace, df, N):
"""
Visualizza i dati simulati con le linee di regressione reali e stimate.
Parameters
----------
trace: `tracepymc.backends.base.MultiTrace`
Un oggetto MultiTrace o ArviZ InferenceData che contiene i campioni.
df: `pd.DataFrame`
DataFrame che contiene i dati
N: `int`
Numero di punti data da simulare
"""
fig, ax = plt.subplots(figsize=(7, 7))
# definisce i tick dell'asse x
x = np.linspace(0, 1, N)
# visualizza le osservazioni di dati simulati
ax.scatter(df['x'], df['y'])
# estrae la pendeza e l'intercetta dalla traccia PyMC
intercepts = trace.posterior.Intercept.to_numpy()[0]
slopes = trace.posterior.x.to_numpy()[0]
# visualizza il grafico di 100 campioni random dalla pendenza e l'intercetta
sample_indexes = np.random.randint(len(intercepts), size=100)
for i in sample_indexes:
y_line = intercepts[i] + slopes[i] * x
ax.plot(x, y_line, c='black', alpha=0.07)
# visualizza la regressione lineare
y = beta_0 + beta_1*x
ax.plot(x, y, label="True Regression Line", lw=3., c="green")
ax.legend(loc=0)
ax.set_xlim(0.0, 1.0)
ax.set_ylim(0.0, 4.0)
plt.show()
if __name__ == "__main__":
# Questi sono i nostri parametri "Reali"
beta_0 = 1.0 # Intercept
beta_1 = 2.0 # Slope
# Simula 100 punti dati tra 0 e 1, con una varianza di 0,5
start = 0
stop = 1
N = 100
eps_mean = 0.0
eps_sigma_sq = 0.5
# Random Seed
s = 42
# Simula i dati "lineari" utilizzando i parametri di cui sopra
df = simulate_linear_data(
start, stop, N, beta_0, beta_1, eps_mean, eps_sigma_sq
)
# Visualizza il grafico dei dati simulati
plot_simulated_data(df)
# Addestra il GLM
trace = glm_mcmc_inference(df, iterations=5000)
# Visualizza il GLM
plot_glm_model(trace)
plot_regression_lines(trace, df, N)
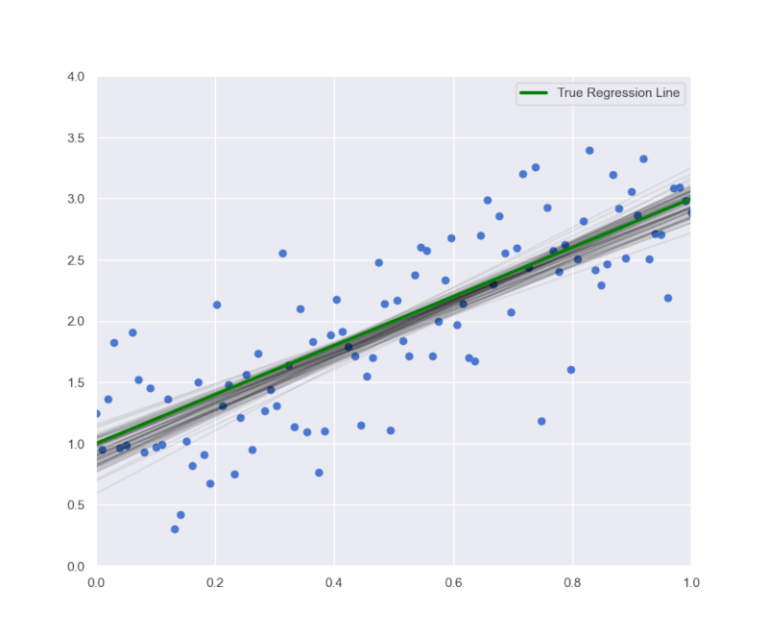
Osserviamo una certa incertezza nella posizione della retta di regressione campionata dal modello bayesiano. Tuttavia, l’intervallo risulta relativamente ristretto e l’insieme dei campioni si avvicina abbastanza alla “vera” linea di regressione.
Conclusione
Nella precedente lezione abbiamo esaminato un semplice metodo MCMC chiamato algoritmo Metropolis. Abbiamo voluto descrivere il funzionamento interno dei vari “algoritmi” MCMC. Consideriamo anche algoritmi come il Gibbs Sampler, l’Hamiltonian Sampler e il No-U-Turn Sampler, tutti molto diffusi nei principali pacchetti software bayesiani.
Alla fine approfondiamo l’approccio ai modelli di regressione lineare bayesiana e ai modelli lineari gerarchici, una potente tecnica di modellazione resa possibile dalle rapide implementazioni MCMC. Dal punto di vista della finanza quantitativa descriviamo anche un modello di volatilità stocastica basato su PyMC e spieghiamo come utilizzare questo modello per creare algoritmi di trading.
Nota bibliografica
James et al. (2013)[4] presentano un’introduzione alla regressione lineare frequentista. Hastie et al. (2009)[2] offrono una panoramica più tecnica, compresi i metodi di selezione dei sottoinsiemi. Gelman et al. (2013)[1] approfondiscono i modelli lineari bayesiani a un livello tecnico avanzato.
Questa lezione trae forte ispirazione dai precedenti post di Thomas Wiecki[6], in particolare nella discussione sui GLM bayesiani, e dai contributi di Jonathan Sedar[5].
Riferimenti
- Gelman, A. et al (2013) Bayesian Data Analysis, 3rd Edition, Chapman and Hall/CRC
- Hastie, T., Tibshirani, R., Friedman, J. (2009) The Elements of Statistical Learning, Springer
- Hoffman, M.D., and Gelman, A. (2011) “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo, arXiv:1111.4246 [stat.CO]
- James, G., Witten, D., Hastie, T., Tibshirani, R. (2013) An Introduction to Statistical Learning, Springer
- Sedar, J. (2016) Bayesian Inference with PyMC3 – Part 1
- Wiecki, T. (2015) The Inference Button: Bayesian GLMs made easy with PyMC3, https://twiecki.github.io/blog/2013/08/12/bayesian-glms-1/

