In questo articolo spieghiamo come implementare una strategia di trading con i modelli ARIMA e GARCH utilizzando il framework DataTrader. I modelli ARIMA e GARCH rappresentano metodologie che trattiamo nel corso sull’analisi delle serie temporali. Eseguiamo il backtest di una strategia di trading sull’indice S&P500, che rappresenta il mercato azionario statunitense. Mostriamo come, combinando i modelli ARIMA e GARCH, possiamo ottenere una sovraperformance significativa rispetto a un approccio “Buy-and-Hold” di lungo periodo.
Strategia di trading con i modelli ARIMA e GARCH
L’idea alla base della strategia è semplice, ma per testarla in modo efficace consigliamo vivamente di leggere il corso sull’analisi delle serie temporali per comprendere i concetti matematici fondamentali.
Applichiamo la strategia su base “rolling”:
- Ogni giorno, al tempo n, utilizziamo i rendimenti logaritmici differenziati dell’indice relativi ai k giorni precedenti come finestra per adattare un modello ARIMA e GARCH ottimale.
- Usiamo il modello combinato per generare una previsione sui rendimenti attesi del giorno successivo.
- Se la previsione indica un rendimento negativo, apriamo una posizione short alla chiusura, mentre se è positiva andiamo long sul titolo.
- Se la previsione ha la stessa direzione del giorno precedente, manteniamo invariata la posizione in essere senza apportare modifiche.
Abbiamo utilizzato l’intero periodo storico disponibile per l’S&P500 offerto da Yahoo Finance, considerando k=500 come parametro iniziale, che possiamo ottimizzare per migliorare le performance o ridurre il drawdown.
Eseguiamo un semplice backtest vettorializzato in Python; pertanto, in un contesto di trading reale, prevediamo performance leggermente inferiori a causa delle commissioni e dello slippage.
Implementazione della strategia
Per implementare la strategia riutilizziamo porzioni del codice sviluppato negli articoli precedenti sull’analisi delle serie temporali finanziarie.
Quando modelliamo serie temporali di dati finanziari, preferiamo modelli autoregressivi come ARMA, ARIMA e GARCH, che usano i dati storici per prevedere i valori futuri. Tuttavia, notiamo che l’applicazione concreta di queste tecniche in strategie di trading operative, confrontate con strategie benchmark come il Buy and Hold, è ancora piuttosto rara. Inoltre, non troviamo facilmente implementazioni pronte all’uso che possiamo replicare su altri asset, mercati o orizzonti temporali.
Per adattare il modello ARIMA+GARCH, seguiamo il metodo classico: prima adattiamo il modello ARIMA e poi applichiamo il GARCH sui rendimenti residui. Otteniamo la previsione finale sommando il contributo del modello ARIMA con quello del GARCH. Iniziamo scaricando i prezzi storici dell’indice S&P500 dal 2000 al 2018 e calcoliamo i rendimenti logaritmici tramite le librerie yfinance, numpy e pandas di Python.
import yfinance as yf
import pandas as pd
import numpy as np
symbol='^GSPC'
start = '2002-01-01'
end = '2018-12-31'
SP500 = yf.download(symbol, start=start, end=end)
log_ret = np.log(SP500['Adj Close']) - np.log(SP500['Adj Close'].shift(1)).dropna()
Una volta ottenuto il DataFrame con i rendimenti dell’indice, creiamo il set di dati relativi agli ultimi k giorni per adattare il modello. Inoltre, creiamo un DataFrame chiamato forecasts per memorizzare i risultati del nostro modello.
# Creazione del dataset
windowLength = 500
foreLength = len(log_ret) - windowLength
windowed_ds = []
for i in range(foreLength-1):
windowed_ds.append(log_ret[i:i + windowLength])
# creazione del dataframe forecasts con zeri
forecasts = log_ret.iloc[windowLength:].copy() * 0
Per convalidare il nostro set di dati, consideriamo che la prima finestra termina il “2003–12–24” e la prima previsione inizia il “2003–12–26”. Allo stesso modo, l’ultima finestra si conclude il “2018–12–28”, mentre produciamo l’ultima previsione con i dati disponibili al “2018–12–29”.
Modello ARIMA+GARCH
Ora che disponiamo dei set di dati e abbiamo definito i nostri target, analizziamo ciascun set per adattare correttamente i relativi modelli statistici. Per questa operazione utilizziamo i pacchetti pmdarima e arch, che installiamo facilmente tramite il comando pip install pmdarima, arch.
Invece di valutare manualmente gli iperparametri (p e q) per ARIMA e selezionare il modello col miglior AIC, usiamo la classe AutoARIMA di pmdarima. Nonostante specifichiamo start_p e start_q, il modello si adatta spesso con p o q pari a zero, perciò adottiamo un approccio manuale classico.
Creiamo quindi una funzione fit_arima che riceve una serie temporale e restituisce il miglior modello, calcolato a partire dagli intervalli scelti per p e q.
import arch
from statsmodels.tsa.arima.model import ARIMA
import warnings
warnings.filterwarnings("ignore")
def fit_arima(series, range_p=range(0, 5), range_q=range(0, 4)):
best_aic = np.inf
best_model = None
best_order = (0, 0, 0)
for p in range_p:
for q in range_q:
if p == 0 and q == 0:
continue
try:
model = ARIMA(series, order=(p, 0, q)).fit()
if model.aic < best_aic:
best_aic = model.aic
best_model = model
best_order = (p, 0, q)
except:
continue
return best_model, best_order
Creiamo ora un ciclo dove richiamare il metodo fit_arima per ogni set di dati, usando i residui per adattare un modello GARCH(1,1). Quindi calcoliamo la previsione di un set per entrambi i modelli. Il risultato finale sarà la somma di entrambe le previsioni.
Nota: questo approccio in due fasi non è l’ideale perchè le parti ARIMA e GARCH devono essere trattate e ridotte al minimo come un unico modello. Tuttavia, python non dispone di una simile libreria.
for i, window in enumerate(windowed_ds):
arima_model, order = fit_arima(window)
arima_pred = arima_model.forecast(steps=1).iloc[0]
resid = arima_model.resid.dropna()
resid = resid[np.isfinite(resid)]
garch = arch.arch_model(resid, vol='Garch', p=1, q=1)
garch_fit = garch.fit(disp='off')
garch_pred = garch_fit.forecast(horizon=1).mean.iloc[-1, 0]
forecasts.iloc[i] = arima_pred + garch_pred
print(f"Date {forecasts.index[i].date()} : Fitted ARIMA order {order} - Prediction = {forecasts.iloc[i]:.6f}")
Una volta calcolate le nostre previsioni, implementiamo il codice per fornire il confronto tra la strategia Buy and Hold e la strategia di trading con i modelli ARIMA e GARCH.
# Memorizzazione dei nuovi segnali calcolati
forecasts.columns=['Date','Signal']
forecasts.set_index('Date', inplace=True)
forecasts.to_csv('prova.csv')
# Otteniamo il periodo che ci interessa
forecasts = forecasts[(forecasts.index>='2004-01-01') & (forecasts.index<='2018-12-31')]
# Calcolo direzione delle previsioni
forecasts['Signal'] = np.sign(forecasts['Signal'])
forecasts.index = pd.to_datetime(forecasts.index)
# Creo un dataframe che contiene le statistiche della strategia
stats=SP500.copy()
stats['LogRets']=log_ret
stats = stats[(stats.index>='2004-01-01') & (stats.index<='2018-12-31')]
stats.loc[stats.index, 'StratSignal'] = forecasts.loc[stats.index, 'Signal']
stats['StratLogRets'] = stats['LogRets'] * stats['StratSignal']
stats.loc[stats.index, 'CumStratLogRets'] = stats['StratLogRets'].cumsum()
stats.loc[stats.index, 'CumStratRets'] = np.exp(stats['CumStratLogRets'])
# Calcolo del confronto con il benchmark
start_stats = pd.to_datetime('2004-01-02')
end_stats = pd.to_datetime('2012-12-31')
results = stats.loc[(stats.index > start_stats) & (stats.index < end_stats), ['Adj Close', 'LogRets', 'StratLogRets']].copy()
results['CumLogRets'] = results['LogRets'].cumsum()
results['CumRets'] = 100 * (np.exp(results['CumLogRets']) - 1)
results['CumStratLogRets'] = results['StratLogRets'].cumsum()
results['CumStratRets'] = 100 * (np.exp(results['CumStratLogRets']) - 1)
buy_hold_first = SP500.loc[start_stats, 'Adj Close']
buy_hold_last = SP500.loc[end_stats, 'Adj Close']
buy_hold = (buy_hold_last-buy_hold_first)/buy_hold_first
strategy = np.exp(results.loc[results.index[-1], 'CumStratLogRets']) - 1
pct_pos_returns = (results['LogRets'] > 0).mean() * 100
pct_strat_pos_returns = (results['StratLogRets'] > 0).mean() * 100
print(f'Returns:')
print(f'Buy_n_Hold - Return in period: {100 * buy_hold:.2f}% - Positive returns: {pct_pos_returns:.2f}%')
print(f'Strategy - Return in period: {100 * strategy:.2f}% - Positive returns: {pct_strat_pos_returns:.2f}%')
import matplotlib.pyplot as plt
columns = ['CumLogRets', 'CumStratLogRets']
plot_df = results[columns]
plot_df.plot(figsize=(15,7))
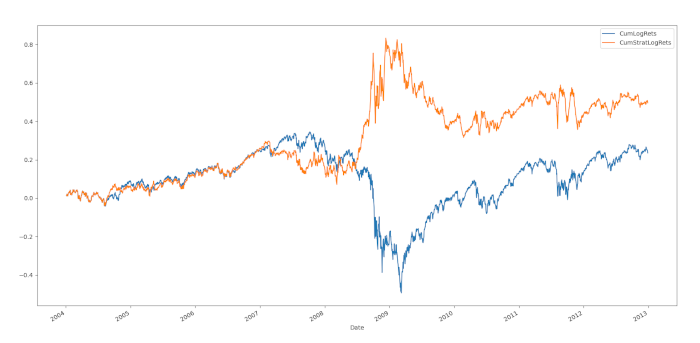
Conclusioni
Nel grafico osserviamo che l’equity della strategia resta sotto il benchmark Buy & Hold per quasi tre anni, ma ottiene ottimi risultati durante il crollo del 2008/2009. Probabilmente in quel periodo si è manifestata una correlazione seriale significativa, che abbiamo catturato in modo efficace tramite i modelli ARIMA e GARCH che abbiamo utilizzato. Dal 2009 il mercato inizia a riprendersi e sembra entrare in una tendenza più stocastica, situazione in cui le prestazioni del modello tornano a peggiorare.
Applichiamo facilmente questa strategia di trading basata su modelli ARIMA e GARCH ad altri indici di mercato, azioni o differenti classi di attività. Ti invitiamo a replicare questo studio su altri strumenti finanziari, perché potresti ottenere risultati persino migliori rispetto a quelli mostrati qui.
Ora che abbiamo terminato l’esplorazione dei modelli della famiglia ARIMA e GARCH, proseguiamo l’analisi affrontando i processi a memoria lunga e i modelli dello spazio degli stati. Approfondiamo anche le serie temporali cointegrate, che ci forniscono modelli capaci di migliorare le nostre previsioni e aumentare la redditività o ridurre il rischio.
Il codice completo presentato in questo articolo, basato sul framework di trading quantitativo event-driven DataTrader, è disponibile nel seguente repository GitHub: https://github.com/tradingquant-it/DataTrader.”